
Полная версия
Tennis Method - Defined Timing

Siegfried Rudel
Tennis Method - Defined Timing
Unit of Perception and Movement
Translated from the original German by
Jürgen Schiffer
1. Edition - 1999
ISBN 9783000042966
PREFACE
At present, interdisciplinary research focusses on behaviour theories: They are dealt with by psychology, biology, sport science, industrial science and anthropological medicine. One of the starting points was V. v. WEIZSÄCKER's Gestaltkreis, which is a theory of perception and movement. Perception and movement form a unit, not only as a sensorimotor functional connection, but also as the working together in comprehensive 'biological acts' or 'per-formances'. As v. WEIZSÄCKER's assistant and successor, I take the liberty to give my opinion on the work presented by Siegfried RUDEL: It is a further development of the Gestaltkreis in the area of movement theory, shown with the example of tennis and the development of a teaching method called 'defined timing'.
Tennis is an interaction game between two opponents which integrates fast ballistic movement sequences. From the point of view of behavioural theory, it is an 'open', complex system. In such systems, there are 'guiding lines', which resemble so-called 'operative systems of representation' and 'inner·models' - i.e. 'schemata' which continuously coordinate the part actions. The author's teaching method is centred around 'defined timing' with gravitation as the connecting factor between perception and movement. As far as time is concerned, form and content are connected by the invariance of gravitation by means of a form movement.
The principle found is related to a special principle of the compositional act of seeing which was found in V.v. WEIZSÄCKER's Gestaltkreis laboratory. For example, fluorescent points moving around in a dark room are perceived by the seeing eye as deviating from their objective course in such a way as one would expect them to move individually and towards each other if they were guided by any physical law. That means that the seeing eye behaves as if it knew this law. V, v. WEIZSÄCKER and his assistants called this principle nomophily or nomotropy.
This behaviour cannot be derived from the classical aestesiophysiologica1 theory of perception and points into a direction which can be assigned to the compository act of performance under more difficult conditions, namely to the special conditions which in the earlier experiments were attached to the 'emptiness' of the field of vision or a more complex move-ment. Similar conditions prevail in the author's investigations on the complex field of interaction in tennis. It is a special biological act which reveals itself in a form principle which could be summed up by the the keyword 'complexity reduction'. Considered as a whole, RUDEL's work can be seen as a confirmation of 'nomophily' (nomotropy) and an expansion of sport science. This and the whole investigation by S. RUDEL will perhaps lead to completely new discoveries.
Prof. Dr.med. P. Christian
Allgemein-klinische und Psychosomatische Medizin
Klinikum der Universität Heidelberg
I. METHOD -
DEFINED TIMING
PRESENTATION OF THE PROBLEM
A tennis teacher stands in front af his pupils and shows them the movement of a stroke. He wants to give them a very detailed demonstration of the movement and performs it very slowly. After this he asks his pupils to imitate the demonstrated movement. The pupils try to do this, the teacher corrects their movements, and after some repetitions the pupils' movements correspond with the teacher's idea. This is an everyday situation, and it is typical of tennis instruction. The learning process seems to be unproblematic since, after a short period of practice, the pupils' movements resemble the movement form demonstrated by the teacher.
After this, the teacher places himself opposite his pupils on the other side of the net and hits the ball to each of them; they are asked to return the ball. The first pupil remembers the movement demonstrated by the teacher well and performs it correctly with the intention to return the ball. However, he misses the ball. "Your movement is correct, but don't forget to hit the ball", is the teacher's comment.
A ball is then hit to the second pupil. He has listened to the teacher's correction and therefore tries to hit the ball at all events. He succeeds in hitting the bali, but the movement form which he practised only a short time ago is hardly recognizable."You hit the ball, but your movement is not correct. Have you forgotten for example the sideways stance?" the teacher asks in order to draw the pupil's attention to one of the movement phases demonstrated by him.
The third pupil now tries to perform the sideways stance, but he hits the ball only with the frame of his racket. The ball disappears behind the fence."Concentrate on hitting correctly! Focus Your eyes on the ball!" And so it goes on. If the pupils perform the movement as it was demonstrated by the teacher, they do not hit the ball; if they hit the ball, their movement form is not correct. Both teacher and pupils are at a loss.
Finally, the pupils do not know anymore which of the teacher's instructions they should follow because everything they do is wrong. The teacher is helpless because none of his advice results in the pupils returning the ball correctly. Is this only a little unimportant tennis story or is there more sense in it?
The dilemma which expresses itself in this interaction between teacher and pupils is the core of a problem which scientists, or better, those with a certain way of looking at science are confronted with. The tennis teacher who demonstrates a movement to his pupils and simultaneously explains it in detail is a phenograph; i.e., he explains the outward picture of the movement as if it were a moving photograph, e.g. the moving arm, the trunk, the knees, etc. In research, too, people try to solve the movement problem by highly exact measurement procedures, by analysing only individual parts of human beings. These investigations are even extended to the nervous system. But even electroencephalographic measurements are basically nothing more than a phenographic way of looking at things, which is an attempt to salve the problem with tape measure and slide-rule, by constantly introducing new parameters and with technical aids.
It is, however, forgotten that every human movement has a meaning. Or, as in the example given above, the teacher succinctly says: "Concentrate on hitting the ball correctly!" However, hitting the ball correctly really consitutes the meaning of the movement. Why is it that the tennis teacher suddenly refers to the hitting, the aim, i.e. the meaning of the movement whereas he usually applies a teaching method which is only oriented to the outward movement? "Concentrate on hitting the ball correctly!" By this statement, the tennis teacher approaches the core of the problem, but his teaching method is not oriented towards this goal. Rather, he considers hitting the ball correctly and mastering it so that it can be played to a point chosen in advance as unimportant or as a matter of course. Only after all instructions have failed is the meaning of the movement considered. Perhaps this example can make clear that there is a discrepancy between the presentation (description) of a movement form and its meaning, which is inherent in this form.
The way of looking at human behaviour whose aim it is to objectivate man is meaning-less! However, to postulate this meaning and to connect it with the movement form must be the very objective of a movement theory which does more justice to man! If movement forms are represented by recording the trace of a body point in a photograph by means of long-term exposure, it is useless if afterwards this trace is measured with all kinds of aids. The objective must be to give a meaning to his trace, to ask for the cause of its coming into existence and in doing so to understand the meaning of this very movement form.
1. DEFINED TIMING: THEORETICAL FOUNDATION
So, the starting point is the meaning of the movement, i.e. hitting the ball correctly, and on this basis it will be attempted to approach the form of the movement. Who or what hits the ball? The racket face hits the ball and not the player's body. If the racket face shall hit the ball, what is meant by hitting it correctly? The ball is hit correctly if it is played to a place chosen in advance. 'Placing' is therefore the optimum result of the meeting of racket face and ball.
This way of asking makes clear what compulsion the movement form is subjected to. The compulsion of hitting the ball with the racket face admits the idea of reducing the movement form to the form of the movement of the racket face in order to be able to examine it better. Under the condition that the ball shall be hit to a certain place, the racket face must perform a compulsive movement in relation to the ball. In doing so, it is the task of the player's body to make possible this compulsive movement, This restricts the body's freedom of movement; but in spite of this, the movement possibilities are immense.
The relationship between racket face and ball, however, restricts the movement of the racket face to a certain form, just as if the racket face were put into a guiding machine (ball behaviour). The player must move in such a way that this 'act of being guided' is not disturbed. This process allows for a multitude of movement possibilities which can only be described as ´Gestalt´. Under the conditions mentioned above, the movement form of the racket represents the player's performance in relation to the moving ball. There must be a relation between the movement of the racket face and the movement of the ball, i.e., the question about the movement form is the question about the relationship existing between the ball which must be perceived by the player and the racket face.
It corresponds with the demand already made by V.v. WEIZSÄCKER (1973, 176): "... then our question is not anymore how spatial relationships can be perceived, but the question rather is: What relationship between the ego and the environment is created by perception?"

Figure 1: The ball as the object of perception
1.1 The ball as the object of perception
It needs no further consideration to identify the ball as the object which the tennis player must focus his eyes on and which he must observe (figure 1). in spite of this, the teaching method which is still used today pretends that the ball does not exist. Although all the player's movement sequences are described in detail, he is kept 'blind'. The instruction "Look at the ball!" only shows the uselessness of this method, which does not make it possible to relate the player's movement form to his perception, which takes place simultaneously. Only if it were possible to establish this relation between the movement of the racket face and the movement of the ball, would the demand to consider perception and movement always as a unit be fulfilled. This means that the movement of the racket face must be related to the movement of the ball, which is the object of perception as far as space and time are concerned. Thus, timing is placed at the centre of attention!
1.2 Ball behaviour - gravitation - possibility theorem of perception
If it proves to be meaningful to consider the ball as the object of perception, what shall and can be perceived of this object must be considered. The possibilities of perception are infinite, even if perception is focussed on the ball. For example, the player can concentrate on the colour, the round form, the shadow of the ball, or on how the ball seems to become bigger or smaller during its flight, or on the rotation of the ball, etc. These are possible perceptions whose selection is, among other things, determined by the wish to find a describable relationship between the movement of the racket face and the movement of the ball. The ball moves in a curve which is a spatial presentation in time and a physical fiction, an imagined line by means of which movements can be can be described. If the player lets his actions be guided by this ball curve, the question occurs whether he is able to do so. Can he perceive the curve of the ball?
V.v, Weizsäcker has shown that the movements which man perceives are not always correspondent with reality, i.e., it is not possiblefor man to perceive arbitrary movements objectively. But, "the.perceiving eye behaves as if it were aware of this law - one could allegorically say - as if it were a mathematician or a physicist". - "We call this behaviour nomophily or nomotrophy ..." (V.v. Weizsäcker 1973, 13). Elsewhere we read: "Perception behaves as if there were a world existing of only two bodies in an empty room which follow the law of gravitation. The eye perceives what physically would be possible" (V.v. Weizsäcker 1973, 264). This possibility theorem means that it is useful to folow the physical principle because this represents one possible way of perception. Since human perception even behaves in such a way if the movement does not follow this principle, it is necessary to examine in how far the real movement, i.e. in this case the movement of the ball, fulfills or follows the law of gravitation. The objective must be to discover the law of gravitation in reality in order to establish a connection between a fact and the perception of this fact. In order to do this, the objective ball behaviour must be looked at. By objective the presentation of certain phenomena under physical conditions is meant. Newton formulates the following laws:
K = m x b bzw. G:= m x g
This means that in a vacuum all things, even if their weight is different, fall to the ground with identical velocity (see the comparison between a feather and a ball). This law holds valid independent of an inertial system moving at a constant speed. What does this mean? A ball which is dropped from a certain height falls with the same velocity as a ball which is dropped from the same hight inside a moving train. An outside observer, however, does not see the vertical fall, but a throwing/flying parabola if the train moves at a constant speed. This is the principle of the independence of translation movements. The importance of the invariance of gravitation and the independence of translation movements can be illustrated by a further example. In figure 2, three ballistic ball curves with different horizontal velocities are shown. The balls are shot off horizontally at the same time, the curves having an identical maximum.
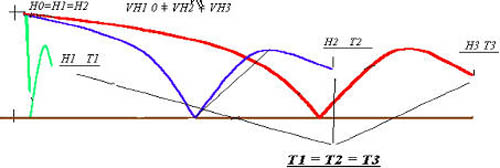
Figure 2: Ballistic ball curves of different horizontal velocities
The first ball is only dropped (VH1 = 0), the second ball is shot off at a slow horizontal velocity (VH2) and the third ball at a higher horizontal velocity (VH3). The silhouettes of these three balls, which are created on a screen which is placed perpendicularly to the level of the ball curve by parallel light coincide with each other. The pictures of the two balls shot off at different horizontal velocities are identical with the movement of the ball which only falls. The balls are at the same time at identicaI heights! The time available to the player is only dependent on the vertical distance covered by the ball.
This phenomenon is expressed in the fall law
H = g/2 t2
and means that the falling movement takes place independently of the respective horizontal velocity.Thus the horizontal component can be looked at separately from the vertical component, Another finding is that a body which is only acted upon by small forces or no forces at all, remains in a state of uniform movement. Since the gravitation force only acts vertically, i.e. perpendicularly to the centre of the earth, and there is no influence of any horizontal force, the horizontal velocity remains constant with such throwing/flying curves (definition of a parabola).
What do these laws mean for the movement of the tennis ball ? If one compares two balls, the one being smoothly struck vertically into the air, the other being hit hard across the field, one finds that with the flight height of the balls being identical the duration of the flight - from striking until landing -is also identical. This means that the time available or striking the ball can be determined by the vertical distance covered by the ball.
This is not the place to explain in detail what deviations the ball is submitted to under consideration of the distance-time behaviour. However, basically it can be said of the so-called ballistic curves (taking into account of friction losses in the air and on the ground with a given form of the ball) that the horizontal velocities of the tennis ball are high as compared with the vertical velocities (exception: high lobs). The reason for this is that the length of the tennis court is very great, whereas the height of fall is not very considerable. A consequence of this is that friction hardly influences the vertical movement of the ball, whereas the horizontal velocity of the ball is considerably reduced by the air resistance (R v2). Although friction proportionally grows with the square of velocity, the decrease in ball velocity is insignificant (up to 4 %). The loss in vertical height, however, is almost identical. Since, however, only the vertical movement is interesting for time orientation, the 'ideal' law of gravitation is almost fulfilled.
Things are different with balls with forward spin (drive/topspin) or backward spin (slice). The so-called ´Magnus effect´, which is characterised by a combination of very high horizontal velocities and high rotational velocities (identical level of direction), changes the behaviour of the ball. In this case the vertical distance-time-law deviates from this phenomenon, and with the simultaneous appearance of spin, the horizontal velocity is responsible for the ball falling to the ground faster or slower. A physical explanation for this is that gravitation is superimposed upon by another force which has its origin in the spin. This means as far as perception is concerned that one sees the ball rising or falling as if in a slow-motion or fast-motion film. Such a ball with 'higher gravitation' has to be corresponded to by the movement of the racket face with a changed vertical velocity. It must be mentioned here that e,g. the topspin, which falls down faster and thus helps to save time, later loses this time again by reaching a higher maximum during bounding (later as far as time is concerned). The importance of this physical fact is that it makes possible for the player to let his movements as far as time and space are concerned be guided by the vertical movements of the ball.
In accordance with the possibility theorem of perception, which implies the idealised movement, and the invariance of gravitation, which even exists under ballistic conditions, there is the possibility to determine the relationship between object and subject as regards time and space. 'Timing' can be defined. Perception and movement can be related to each other. The structural problem of form is solved with the example of a concrete movement. The required unit of perception and movement (see Rudel 1977, teaching film) can be expressed in a 'graspable' relationship.
In order to explain once again the connecting character of gravitation as far as perception and movement are concerned, it must once more be stated which perception and which movement are meant. The movement is the flight of the ball with its invariance in the vertical aspect and the movement af the racket face. They are connected in the 'guiding-beam movement' of the racket face, in the 'sticking', in the simultaneous 'drawing', or whatever image one uses.
1.3 Contact movement racket face - ball
It has already been mentioned that the player's movement is the establishment of a relation between himself and the ball. This relation is established evem before the player touches the ball with the racket face by orienting to the opponent's stroke and the behaviour of the ball during the flight. The better the player adapts his movements to the behaviour of the approaching ball as far ds space and time are concerned, the more exactly ('timed') can the stroke be performed. The demands on the relationship to be described must encompass all space-time relations between player and ball before, during and after hitting the ball. In doing so, the contact movement between racket face and ball is helpful.
Just imagine the following situation: Two players are standing opposite each other, one of them perpendicularly strikes the ball up to the height of his head. It is the other player's task to catch the falling ball with the racket face so that the ball does not hounce.
From this the following movement sequences are developed:
• striking perpendicularly downward when the ball is rising or falling above net height;
• striking perpendicularly upward when the ball is falling for the first time;
• hitting perpendicularly upward after the ball has touched the ground and is rising again (figure 3);
• hitting perpendicularly upward after the ball has touched the ground and is falling for the second time.
Figure 3 : Half-volley - vertical aspect
In order to catch the ball smoothly, the velocity of the movement of the racket face must correspond with the velocity of the ball. If the player right from the time of his partner's stroke tries to follow the vertical movement of the ball with his racket face, the approach to identical height when the ball falls can easily be achieved. In order to perform this movement, the space-time-relation can be determined. In doing so, the 'timing' of the racket face movement represents the performance of the movement of the whole body. This acquired vertical contact behaviour is also used when performing the movement sequences mentioned above:



