
Полная версия
Фридрих: VLS (RLS) за полгода. Часть 3. Winter Variation, No Edges, Summer Variation, Edge Control

Фридрих: VLS (RLS) за полгода. Часть 3
Winter Variation, No Edges, Summer Variation, Edge Control
Станислав Баранов
© Станислав Баранов, 2020
ISBN 978-5-4498-9228-7 (т. 3)
ISBN 978-5-4498-1632-0
Создано в интеллектуальной издательской системе Ridero
Введение
Данная книга написана с целью собственного обучения и в качестве учебного пособия для школ спидкубинга.
Для того, чтобы формулы были выучены на уровне мышечного запоминания (навыков и рефлексов) и их необходимо первоначально выучить. Вот именно в первоначальном заучивании у многих начинаются проблемы, которые многие решают по разному. Метод изложенный в данной книге позволит выучить формулы для первоначального заучивания и позволит применять формулы без «подглядывания», что в свою очередь, сделает ваши тренировки более эффективными, и сможете добиться выполнения алгоритмов за секунды и доли секунды. Выучив алгоритм с помощью запоминалки, Вы сможете натренировать его, используя любое свободное время (в транспорте, в очереди и т.п.).
Данная книга это третья часть алгоритмов из RLS (VLS) (Valk и/или Rowe Last Slot) с готовой парой «кувалда» и «трехходовки». В этой части рассмотрены случаи Edge Control, WINTER VARIATION, NO Edges и SUMMER VARIATION (трехходовка). Название пар я взял из второй части моей книги о методе Фридрих Метод Фридрих за месяц: F2L.
В главе про SUMMER VARIATION я написал, почему включил данную главу в эту книгу (дополнительный аргумент каждая книга содержит по три главы не считая Edge Control).
Здесь приведу аргумент с сайта https://www.speedsolving.com/wiki/index.php/OLS почему нужно изучать RLS (автоматический перевод).

Аргументы изучения VLS (RLS)
В некоторых местах в части главы «Как запомнить?» иногда будут пропуски (например, на момент публикации книги придуманы запоминалки для двух из трёх алгоритмов) постепенно многие пропуски будут заполнены, а у читателя пока есть возможность предложить свой вариант и попасть в книгу (при очередной публикации).
История создания метода
Эту главу дописал в книгу после дискуссии со спидкубером Кириллом Литвиновым (псевдоним на ютубе Кшиук). Он утверждает, что необходимо оставить одно название RLS. Я считаю, что метод одновременно придуман несколькими людьми, но основную работу сделали два человека Mats Valk, Rowe Hessler. Lucas Winter придумал алгоритмы последнего слоя впоследствии названные Winter Variation.
Вот ссылка на статью Википедии спидкубинга https://www.speedsolving.com/wiki/index.php/VLS.
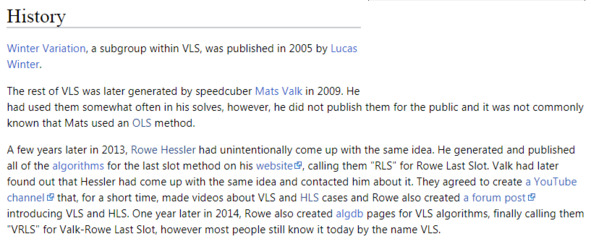
Фрагмент с сайта
Перевод статьи
Винтер Вариашн (Winter Variation) субгруппа VLS была опубликована Лукасом Винтером (Lucas Winter) в 2005 году.
Другая часть VLS позже была сгенерирована спидкубером Матсом Валком (Mats Valk) в 2009 году. Он часто использовал их в своих сборках, однако, он не публиковал их для широких кругов публики и спидкуберам было известно, что он использует OLS метод.
Нескольким годами позже, в 2013 Роу Хесслеру (Rowe Hessler) непреднамеренно выступил с той же идеей. Он сгенерировал и опубликовал все алгоритмы для метода последнего слоя на своём веб-сайте, назвав их RLS, что значит Rowe Last Slot (последний слот Роу). Позже Валк обнаружил, что Хесслер пришёл к той же идее и связался с ним по этому поводу. Они согласились создать Ютуб-канал об этом, в течении короткого времени сделали видео о VLS- и HLS-случаях и Роу также создал форум, на котором представил VLS и HLS. Годом позже, в 2014, Роу также создал страницы на сайте algdb для VLS-алгоритмах, окончательно назвав их VRLS, что означает Valk-Rowe Last Slot, однако большинство людей с того времени знают алгоритмы сегодня под именем VLS.
Примерно такую же историю можно услышать от Матса в его интервью Максиму Чечневу по поводу VLS. Интервью Матса Валка Mats Valk на чемпионате Welcome to Academy 2018 Вопрос про VLS на 4:45, о том, как придуман способ. (https://www.youtube.com/watch?v=ZWhGFoSySDI).
Для того, чтобы признать заслуги всех создателей, я использую в названии книги VLS (RLS) и есть глава Winter Variation, которое также использовано в названии книги.
Структура книги и написание формул
Очень частый вопрос и совет использовать английский апостроф при написании формул.

Из переписки с читателем
Но к сожалению встроенный редактор многих редакций переведет автоматически все буквы с апострофом в буквы с кавычкой.
Вот пример картинки из многих редакторов. Это еще наилучший вариант, другие редакторы переводят ещё хуже и формула становится совсем непонятной.
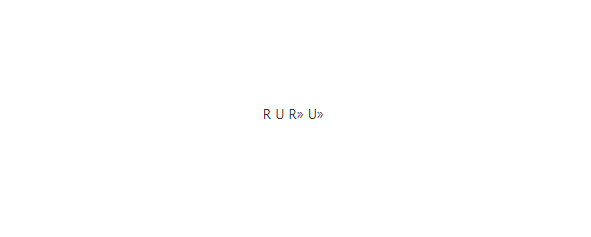
Фрагмент из редактора книги и сайтов
Автор уже что-то только не перепробовал и принял решение писать с единичкой в верхнем индексе. Тогда многие реакторы более менее справляются с формулами с наименьшим искажением.
Есть конечно рисовать все формулы как картинку, но это огромный труд и пока у автора нет на это времени. Так что читателям придется мириться с написанием формул с единичкой в верхнем индексе вместо штриха.
Глава книги (кроме вспомогательных глав) содержит ответы на следующие вопросы: 1) как выглядит (как различать); 2) как решить (алгоритмы); 3) как запомнить алгоритм или формулу алгоритма; 4) как смоделировать ситуацию.
С учетом развития интернета книга будет написана с некоторым повтором или будет отсутствовать красота изложения (литературность). Это сделано для того, чтобы книга давала правильный ответ на поисковые запросы и хорошо индексировалась роботами-поисковиками. Прошу читателя сразу за это простить.
Формулы и как их запоминать
Для запоминания каких-либо частей формулы, иногда пиф-пафов, мной придумана таблица соответствия букв русского алфавита и направлений вращения.
Вот эта таблица 1
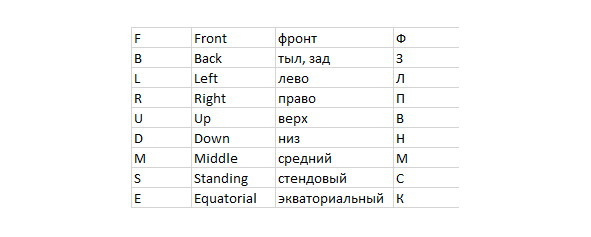
Таблица 1. Азбука вращений
Вращение средних слоёв, как запомнить?
До начала изучения формул необходимо показать вращение средних слоёв. Разумеется вращение этих слоёв можно посмотреть и в других источниках, но мне хочется чтобы книга была самостоятельным руководством, без необходимости отвлекаться.
Частота применения (одни чаще, другие реже) вращения этих слоёв и определило очередность рассмотрения.
Вращение среднего слоя M. Этот средний слой находится между правой R и левой L гранями. Направление вращения M слоя совпадает с направлением вращения грани L.
Вращение среднего слоя S. Этот слой находится между передней F и задней B гранями. Направление вращения слоя S совпадает с направлением вращения грани F. Вращение среднего слоя E. Этот слой находится между нижней D и верхней U гранями. Направление вращения слоя совпадаем с направлением вращения грани D. Это означает, что направление по часовой и против часовой стрелке совпадает с направлением соответствующей грани. Всё понятно, но как это запомнить?
Для запоминания вышесказанного я придумал следующую фразу запоминалку
«EDет MаLая SоFа»
Можете взять эту запоминалку или придумать свою, думаю принцип понятен.
Читатель может заметить, слои вращаются по часовой и против часовой стрелки.
Для обозначения направления вращения автор использовал гласную букву, разделив все буквы на две группы. Первая группа (буквы а, о, у, ы, э) отвечает за направление вращения по часовой стрелке. Вторая группа (буквы е, ё, и, ю, я) отвечает за направление против часовой стрелки.
Чтобы запомнить какие-буквы за какое направление отвечают, автор придумал две запоминалки. Все эти сведения отражены в таблице 2.
Таблица 2. Направление вращения

Соответствие букв направлению
С помощью этих двух таблиц (первая содержит согласные буквы, вторая гласные буквы) можно для частей формулы придумывать буквосочетания, и по ним придумывать образы. В таблице 3 приведены несколько таких примеров кодировки символов образами.
Таблица 3. Примеры кодирования
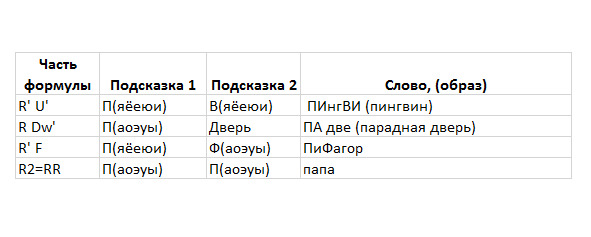
Примеры кодирования
Таким способом можно перекодировать упрямые незапоминающиеся места любых формул. Все запоминалки нужно представлять в виде образов, картинок или видео-образов, только так надежно запомнится формула алгоритма.
Например, U2 как наиболее частая комбинация будет кодироваться словом «Вова».
Необходимость пиф-пафов
Пиф-пафами называют несколько любых ходов подряд. Любые несколько ходов имеют свой цикл, через которые кубик возвращается в первоначальное положение. Обычно берут частовстречающиеся комбинации ходов. Пиф-пафы помогают разбить формулы на условные последовательности (их называем пиф-пафами), которые помогают запомнить сложную формулу и/или связаны удобным движением пальцев (фингертрикс).
Главу о пиф-пафах я поместил в конец книги в качестве справочной информации.
Edge control с готовой парой
Применение Edge control
В первых изданиях книг эта глава планировалась только в третьей части. Но по мере изучения VLS я убедился в необходимости данной главы на всех этапах изучения VLS. Его нужно применить (сделать одну 8 формул), если Вы забыли алгоритм для конкретного случая.
UF VLS
(отсутствует ребро UF)
Самая короткая формула из всех алгоритмов UF VLS будет решение случая Квадрат 220 (UF15) – Кувалда

Квадрат 220 (UF15) – Кувалда
Решение
R1 F R F1
Это решение расставит только 4 ребра шапки, и нужно будет решить один из 7 случаев крестовых OLL.
U* VLS (отсутствует ребро U*)
UB VLS
(отсутствует ребро UB)
Выбор самой короткой формулы для случая UB VLS очень большой. есть несколько формул одинаковой длины – 6 ходов:
Решение
1_6) y1 U2 (R21 F R F1) R
2_6) U2 F2 (Rw U Rw1) F
3_6) U y F (R U1 R1 F1)
4_6) U R y (R U1 R1 F1)
5_6) (U R B) (U1 B1 R1)
6_6) (U Lw U) (F1 U1 Lw1) = (U Lw – U F1 – U1 Lw1)
1) и 2) это решение случая Галстук 100 (UB05)

Галстук 100 (UB05)
3) – 6) это решение случая Боковой квадрат 200 (UB19)

Боковой квадрат 200 (UB19)
Стоит еще рассмотреть 7-ходовые решения
7_7) U (F1 L1 U2 L U F)
8_7) (y1 U) R1 F1 U2 F U R=Dw R1 (F1 U2 F U) R
9_7) (F1 U2 F U) (R U R1)
7) – 8) это решение случая Боковой квадрат 600 (UB17)

Боковой квадрат 600 (UB17)
9) это решение Галка 211 (UB22)

Галка 211 (UB22)
Любое решение расставит только 4 ребра шапки, и нужно будет решить один из 7 случаев крестовых OLL.
Можно просто поставить пару антипиф-пафом (U R U1 R1) и выйти на OLL с двумя усами креста.
UL VLS
(отсутствует ребро UL)
Самое короткое решение в 6 ходов
1_6) U – F1 (L1 U1 L) F
2_6) y1 U (R1 F1 – U1 F R) = Dw (R1 F1 – U1 F R)
Есть еще решения в 7 ходов
3_7) U (F1 U2 F) (R U1 R1)
4_7) R1 U1 (F U R U1) F1 = (R1 U1 F) – U – (R U1 F1) = (R1 U1 F U R) – U1 F1
это
1) – 3) это все решения для Клюшка 200 (UL19).

Клюшка 200 (UL19)
4) это решение для Жирная Т 200 (UL06).

Жирная Т 200 (UL06)
Автор использует второе решение (правша).
Любое решение расставит только 4 ребра шапки, и нужно будет решить один из 7 случаев крестовых OLL.
Можно просто поставить пару антипиф-пафом (U R U1 R1) и выйти на OLL с двумя усами креста.
UBUL VLS
(отсутствуют ребра UB и UL)
Самая короткая формула для случаев UBUL VLS это решение для случая Совок 301 (UBUL16) в 7 ходов.

Совок 301 (UBUL16)
1_7) (U x1 (R2 U1 R1 U) x U1) – R1
2_7) U R – (R B1 R1 B) – U1 R1 = U (R2 B1 R1 B) – U1 R1
3_7) х1 – F R (R U1 R1 U) F1 R1 – x = х1 – F (R2 U1 R1 U) F1 R1 – x
4_7) y U – (F2 R1 F1 R) – U1 F1 = y – U F (F R1 F1 R) U1 F1
Автор использует 4-ю формулу, так как там наименьшее число перехватов и автор не любит ходы B и B1.
Дальше предлагать другие формулы не имеет смысла – в них будет 8, 9, и т.д ходов.
Любое решение расставит только 4 ребра шапки, и нужно будет решить один из 7 случаев крестовых OLL.
Если поставить пару антипиф-пафом (U R U1 R1) и выйти на OLL с двумя усами креста. Будут установлены два ребра напротив друг друга (различные виды палок).
U* VLS (отсутствуют рёбра U* и U*)
UFUB VLS
(отсутствуют рёбра UF и UB)
Оказалось, что самый короткий и единственным хорошим случаем UFUB VLS будет случай Пловец 920 (UFUB11), к которому сводятся многие случаи VLS.

Пловец 920 (UFUB11)
1_7) R1 F R2 U R1 U1 F1 = (R1 F R *) (R U R1 U1) F1
В этой главе не буду писать как запомнить. Это уже сделано в соответствующей главе.
Любое решение расставит только 4 ребра шапки, и нужно будет решить один из 7 случаев крестовых OLL.
Можно просто поставить пару антипиф-пафом (U R U1 R1) и выйти на OLL с двумя усами креста.
UFUL VLS
(отсутствуют рёбра UF и UB)
Здесь нет даже 7-ходовых решений. Есть только несколько 8-ходовых решений.
1_8) y1 U1 – R D (Rw1 U Rw) D1 R1
2_8) Dw (R2 D1 L – F1 – L1 D R2)
3_8) y1 U – R2 D1 (Rw U1 Rw1) D R2 = Dw – R2 D1 (Rw U1 Rw1) D R2
4_8) R1 U1 F U R2 U1 R1 F1 = (R1 U1 F U R) – (R U1 R1 F1)
1) это решение самого первого случая Стрелка Т 410 (UFUL01)
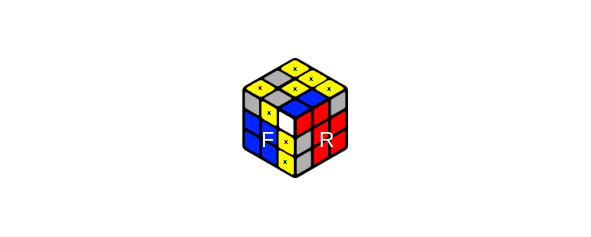
Стрелка Т 410 (UFUL01)
2) – 3) это решение Тетрис Т 910 (UFUL06)

Тетрис Т 910 (UFUL06)
4) это решение Тетрис Т 320 (UFUL07)

Тетрис Т 320 (UFUL07)
Любое решение расставит только 4 ребра шапки, и нужно будет решить один из 7 случаев крестовых OLL.
Можно поставить пару кувалдой (R1 F R F1) и выйти на OLL с двумя усами креста.
No edges VLS
(отсутствуют все рёбра)
К сожалению нет даже 8-ходовых решений.
Вот 9-ходовое решение случая Скальпель 210 (NE19)

Фрагмент из книги «Фридрих: VLS (RLS) за полгода. Часть 3»
1_9) U2 – (x U1 (Rw1 U2 Rw) U x1) (R U2 R1)
2_9) U2 – (F1 L1 U2 L F) – (R U2 R1)
Кроме 9 ходовых решений есть красивое 10-ходовое решение
3_10) U2 (R1 F R F1) – U2 (R1 F R F1)
Алгоритм 3) это решение случая Точка (пуля) 211 (NE24)

Точка (пуля) 211 (NE24)
Любое решение расставит только 4 ребра шапки, и нужно будет решить один из 7 случаев крестовых OLL.
В любом случае поставив пару (R1 F R F1) можно выйти на OLL с двумя усами креста.
All edges VLS
(все рёбра присутствуют)
Последний случай, который нужно рассмотреть в Edge Control, это когда все рёбра на месте. Кажется ведь все рёбра на месте для чего нужно применять Edge Control. Но в то время как мы будем устанавливать последнее ребро, нужно сохранить остальные и установить последнее.
Единственный хороший и короткий алгоритм сохранения остальных рёбер при установке последней пары и ребра шапки я нашёл на сайте http://www.cyotheking.com/.
1_7) Lw1 (U2 R U2 Rw1) U2 L
Альтернатив данному решению я на данный момент не нашел (есть решения 8-и и 9-ти ходовые). Это решение случая Полный 400 (WVLS01)
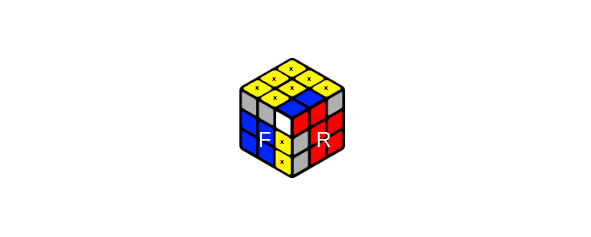
Полный 400 (WVLS01)
Для тренировки нужно знать, что этой формулой случай моделирует сам себя.
Тем, кто пока не запомнил данную формулу напишу, что для сохранения жёлтых рёбер шапки и установки достаточно сделать антипиф-паф (U R U1 R1).
Пиф-паф (U2 R U2 R1) также установит пару и все 4 ребра.
VLS
Классификация и моделирование
Распознавать ситуации VLS будем по верхней шапке (так как различают случаи OLL) и рисунку из цвета наклеек шапки на блоке, образованному из рёбра FR и трёх других мест.
Уже после написания большого количества глав мне пришла в голову идея классифицировать и оцифровать случаи по признакам наличия (отсутствия жёлтых наклеек) на определенных местах и их рисунку.
Обозначим эти места по видимости и значимости места:
1) блок состоящий из угла FRD и ребра FR (стороны F и R);
2) сторона F блока, состоящего из углов FUL и ребра FU
3) сторона R угла RUB.
Теперь подробно рассмотрим возможные случаи возникающие на этих местах.
На первом местоположении возможны следующие комбинации:
1а) точка правая (прямая);
1б) точка левая (обратная);
2а) блок прямой (две правые наклейки);
2б) блок обратный (две левые наклейки);
3а) шахматы прямые;
4а) шахматы обратные.
Первое местоположение.
Вот как это выглядит:
Точка правая на первом местоположении (ребро FR)

Точка правая на первом местоположении (ребро FR) – код 1
Точка левая на первом местоположении (ребро FR)

Точка левая на первом местоположении (ребро FR) – код 3
Блок прямой (две правые наклейки)

Блок прямой (две правые наклейки) на первом местоположении – код 2
Блок обратный (две левые наклейки)

Блок обратный (две левые наклейки) на первом местоположении – код 4
Шахматы прямые

Шахматы прямые на первом местоположении – код 6
Обратные шахматы на первом местоположении

Обратные шахматы на первом местоположении – код 9
Второе местоположение.
На втором местоположении возможны только три комбинации:
1) там нет жёлтых наклеек на стороне F;
2) Точка;
3) блок (две наклейки).
Вот как это выглядит:
Точка на втором местоположении

Точка на втором местоположении – код 1
Блок на втором местоположении

Блок на втором местоположении – код 2
На втором местоположении возможна ещё одна точка, но для неё не стал вводить кодировку, так как по рисунку OLL понятно о какой точке будет идти речь. Для такой точки тоже код будет 1.

Точка-ребро на втором местоположении – код 1
Третье местоположение.
На угле (третьем местоположении) возможны только две комбинации:
1) там нет желтой наклейки (она либо на шапке, либо на стороне В);
2) точка.
Вот как выглядит точка на третьем месте, когда там точка:

Точка на третьем местоположении – код 1
Сами комбинации тоже оцифруем, чтобы потом по цифрам быстро понимать какая перед нами ситуация и быстро вспомнить алгоритм.
Цифрой 0 обозначим отсутствие наклейки. Цифрой 1 обозначим точку – одну наклейку. Цифрой 3 обозначим точку – одну наклейку слева на втором местоположении. Цифрой 2 обозначим блок 2 правые наклейки. Цифрой 4 обозначим блок 2 левые наклейки.
Цифрой 6 обозначим прямые шахматы (2 наклейки: одна наклейка на стороне R ребра FR, другая на стороне F угла FRU). Цифрой 9 (перевернутая 6) обозначим обратные шахматы (2 наклейки: одна наклейка на стороне F ребра FR, другая на стороне R угла FRU).
Первом местоположении всегда есть хотя бы одна наклейка на ребре FR, поэтому классификация никогда не будет начинаться на ноль.
Моделирование ситуации всегда происходит на собранной шапке (или собранном кубике). Это всегда последняя часть главы, так как опытные спидкуберы легко моделируют случай по формуле и эта часть написана исключительно для начинающих спидкуберов.
3 рёбра ориентированы (WINTER VARIATION)
Нужно запомнить весь список группы ориентированных рёбер (WINTER VARIATION). Для этого нужно связать в одной истории все названия подгрупп: полный, доска, трубка, камера, бегущий, голосующий, довольный, крест.
Полный для меня это образ актёра Жерара Деперьде.
Можете сами придумать подобную историю: «Жерар Депардье крутит кубик (на кубике алгоритм случая Полный). Жерар Деперьде катается на роликовой доске. Одновременно он рассматривает коллекцию курительных трубок. На камеру он снимает других актёров: бегущего, голосующего, довольного (улыбающегося и показывающего знак ОК) и крестящегося крестоносца».
История примерная (мне нужно ещё соблюсти правила публикации). Каждый раз вспоминая эту историю, она будет обрастать новыми деталями и прочнее запоминаться.
Но самое интересное, что каждую группу можно условно разбить на 8 условных подгрупп. Не знаю, делал ли так, кто-то из изучающих и придумавших метод, но в своих книгах я так сделал. Как же так 8 групп, а алгоритмов 27. Ведь 27 не делится на 8. Но каждая подгруппа содержит количество алгоритмов, определяемых степенью 2n, где n=0, 1, 2, 3: 1, 2, 4 или 8 алгоритмов.
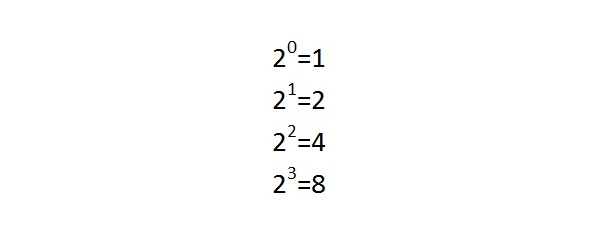
Число алгоритмов в группе VLS









