Космос. Иллюстрированная история астрономии и космологии

Были, естественно, предприняты попытки связать параметры описанного механизма с теорией Гиппарха, и одной из наиболее примечательных особенностей этого устройства является использование в нем эпициклического расположения колесиков. Как следует из надписи на кожухе, этот инструмент принадлежал к разряду того, что обычно называли парапегмой (мы уже встречались с этим термином, говоря о календарях, публично выставляемых в Афинах). Существовало много разновидностей парапегм. Одни известны нам по документам, написанным на папирусе, другие – по надписям в общественных местах, например на водяных часах. Парапегмы могли информировать население об очередности погодных изменений, согласованной с первыми или последними появлениями тех или иных созвездий и ярких звезд в течение солнечного года. По отдельным словам, которые удалось расшифровать, можно понять, что указывались также направления ветра, случайным образом увязанные с записями о наступлении затмений.

Похожие приспособления, как известно, существовали и в более поздние времена – в Византии и мусульманских государствах, и в этом можно увидеть некую прерывистую преемственность, но все это не шло ни в какое сравнение с механическим устройством, изготовленным не позднее XIV в., – часами в городе Сент-Олбансе (см. с. 369). Такие устройства были скорее следствием, чем причиной развития теоретической астрономии, которая, по всей видимости, не слишком продвинулась к тому времени, когда изготовили Антикитерский механизм, и оставалась таковой еще в течение двух столетий. Конечно, мы не должны судить о полном отсутствии значимых астрономических достижений, исходя только из нашей неосведомленности о них. В поколениях, предшествовавших Птолемею, был как минимум один человек, которого мы не можем обойти вниманием, а именно – Менелай Александрийский. Расцвет его деятельности пришелся на 100 г. до н. э. Мы почти ничего не знаем о его жизни, кроме того факта, что он побывал в Риме и сделал несколько астрономических наблюдений, и сегодня его помнят главным образом как математика, а также как человека, доказавшего теорему, оказавшую бесценную помощь всем, кто желал выполнять серьезные вычисления в сферической астрономии. Те, кто знаком с теоремой Менелая только для плоского треугольника, пересеченного прямой, может не знать, что это только частный случай более общей подобной теоремы, в которой прямые линии заменены большими кругами на поверхности сферы. Если в теореме для плоского треугольника мы учитываем только длины отрезков, то в сферической интерпретации нам приходится учитывать хорды дуг. Птолемей успешно использовал сферический случай теоремы Менелая. Он и в самом деле с одинаковым рвением усваивал все самое лучшее из работ своих предшественников. Его вряд ли можно обвинить в том печальном факте, что ореол славы, окружающий его имя, так часто затмевал вклад других астрономов в его достижения.

Астроном, математик, астролог и географ Клавдий Птолемей родился около 100 г. н. э. и умер спустя примерно 70 лет. Его имя – Птолемей – свидетельствует о том, что он был египтянином греческого происхождения или по меньшей мере человеком, приобщенным к греческой культуре через своих предков; в то время как его имя – Клавдий – ясно говорит о наличии у него римского гражданства. Его астрономические работы посвящены некоему «Сиру», не упомянутому в других источниках, а в числе его прямых учителей был, по-видимому, некий Теон, от которого он, по его собственному признанию, получил записи планетных наблюдений. Помимо этих очевидных фактов о его личной жизни, нам почти ничего не известно. (Не нужно путать упомянутого здесь Теона с отцом Гипатии. Теон, Птолемей и даже Клеопатра – распространенные египетские имена. Арабские и латинские писатели Средневековья часто упускали из внимания этот факт и ошибочно принимали Птолемея-астронома за царя, изображая его с короной на голове, как показано на ил. 59.)

59

Распространенное заблуждение: Птолемей в обличье царя. Фрагмент ксилографии Грегора Рейша из книги «Margarita Philosophica» (1503). Персонифицированная Астрономия объясняет астроному, как пользоваться квадрантом.

Объемные сочинения Птолемея дают основание предположить, что он замыслил составить энциклопедию по прикладной математике. Его книги по механике известны нам только по названиям. Большая часть его «Оптики» и «Планетных гипотез» может быть восстановлена по фрагментам, собранным из греческих и арабских источников. Некоторые не столь объемные работы по теории геометрической проекции («Аналемма» и «Планисфера»), равно как и капитальный труд «География», сохранились на греческом языке, то же самое можно сказать о его знаменитом астрономическом трактате «Альмагесте».

Само название этой наиболее выдающейся из его работ заслуживает внимания как индикатор культурных перемен. Она была начата в Греции с исходным названием «Математическое сочинение» и затем стала «Великим (или Величайшим) сочинением». Когда в IX в. арабы перевели его на свой язык, в качестве названия оставили только одно слово – «Величайшее», приближенно напоминающее греческое слово мегисте, после чего оно стало называться ал-маджисти. Отсюда через латинское название Almagesti или Almagestum, присвоенное ему в XII в., оставалось сделать только один шаг до привычного нам «Альмагеста».

Этот труд, состоящий из тринадцати книг, начинается с изложения фундаментальных положений, которые в основном служили подтверждением философии Аристотеля, хотя в них было заметно и влияние стоицизма. Нравственные идеи, отмечает Птолемей, – это то, чего каждый из нас может достичь, не прибегая к особым средствам, а для понимания Вселенной мы должны изучить теоретическую астрономию. Вслед за Аристотелем он помещает физику на низший уровень, поскольку она имеет дело с переменчивым и подверженным разрушениям нижним миром. В отличие от этого, астрономия служит теологии, поскольку она обращает наше внимание на Первопричину небесных движений – божественный Перводвигатель. Заканчивая это довольно краткое философское введение, Птолемей переходит к некоторым весьма отвлеченным космологическим аргументам качественного характера, касающимся небесной сферы и различных наблюдаемых на ней движений. Здесь он опять более или менее следует Аристотелю, повторяя его физические аргументы о сферической поверхности, центральном положении и неподвижности Земли. Кроме того, Птолемей разбирает вопрос о чрезвычайно малых размерах Земли по сравнению с небесами. Он не ссылается на рассуждения Эратосфена и Посидония на эту тему (Посидоний был чрезвычайно влиятельным астрологом и философом-стоиком; он родился около 135 г. до н. э.).

То, что Птолемей не упоминает об этих более ранних авторитетных источниках, заслуживает особого внимания, поскольку близкий современник Птолемея Клеомед рассказывает об измерениях, произведенных Эратосфеном, и в той же работе пишет о рефракции световых лучей, проходящих через земную атмосферу. Похоже, Птолемей просто не знал об этом авторе. Клеомед, как обычно полагают, первооткрыватель атмосферной рефракции – явления, имеющего огромное значение в астрономии. В своем «Альмагесте» Птолемей рассматривает рефракцию только в связи с размерами небесных тел при их наблюдении вблизи горизонта. В «Оптике» он подробно разбирает теоретические аспекты атмосферной рефракции, но это была его поздняя работа.

Затем следует математическое введение с изложением теоремы Менелая и таблицей хорд со значениями до трех значащих цифр в шестидесятеричной системе, а также другими разделами, которые мы сегодня отнесли бы к категории «тригонометрических». Его таблица, составленная с интервалом в половину градуса, базируется на значении хорды, соответствующей 1°, точно определенном им методом последовательных приближений. Вскоре после этого, в первой и второй книгах «Альмагеста», он на практике демонстрирует применимость перечисленных им математических методов к решению астрономических задач, и одним из вопросов, регулярно возникающим как в первых, так и во всех следующих книгах, является расчет угла наклона эклиптики к небесному экватору.

Используя крайние отклонения Солнца, он нашел, что значение этого фундаментального параметра должно лежать в интервале между 23;50° и 23;52,20°. В итоге он остановился на величине 23;51,20°, попадающей в этот диапазон, но не являющейся точной. (Точнее было бы 23;40,42°.) Он, как полагают некоторые, выбрал это значение, поскольку Гиппарх (и даже Эратосфен) считали его правильным. Удивительно, если бы Эратосфен сумел определить это значение точнее, чем 24°. Инструменты Птолемея были несовершенны, и, вероятно, он примерно догадывался насколько. Есть один очень важный вопрос – мог ли он допустить, чтобы восхищение, выказываемое им в отношении Гиппарха, поколебало его собственное суждение или же поставило под сомнение показания его инструментов. Однако мы не располагаем никакими данными о том, каково было мнение самого Гиппарха по поводу этой величины.

В третьей книге «Альмагеста» Птолемей признает справедливость солнечной теории Гиппарха. Он сравнил данные собственных наблюдений равноденствий с полученными Гиппархом; кроме того, он сравнил наблюдения солнцестояний с аналогичными наблюдениями, проведенными Метоном и Евктемоном в 432 г. до н. э., то есть примерно шестью столетиями ранее. При этом он ошибся в календарных расчетах примерно на одни сутки, но даже этого оказалось достаточно, чтобы он, отбросив собственное неверное значение, полученное им для тропического года, еще раз убедился в правоте Гиппарха и принял его значение – 365¼ суток за вычетом 1/300. Это оказалось больше истинного значения на шесть временны́х минут (на деле – 6;26 минут), однако теория позволяла достаточно хорошо рассчитывать большинство солнечных явлений, и вряд ли он помышлял о том, чтобы каким-либо образом поменять ее. Начиная с IX в. мусульманские астрономы стали предпринимать попытки уточнения этой величины, несколько таких попыток было сделано в средневековой Европе, все полученные значения оказались более или менее близки к истинному. Можно только сожалеть о том, что значение, полученное Птолемеем для солнечного движения, неразрывно связано с параметрами лунного и планетного движений, равно как и с параметрами прецессионного движения звезд. Указанная взаимозависимость параметров всегда оказывалась серьезной проблемой для астрономов, которые не обладали редкой привилегией начинать все с чистого листа и были вынуждены опираться на данные, полученные в предыдущие исторические периоды.

ДВИЖЕНИЕ СОЛНЦА ПО ПТОЛЕМЕЮ

Птолемей прилагает таблицы, позволяющие быстро вычислять два угла, необходимые для нахождения положения Солнца. Использованные им методы были впоследствии распространены на более сложное движение планет и предвосхитили появление идеи создания общей теории небесного движения. Для Солнца требуется знать два исходных параметра, а третий мы введем чуть позже. В простейшей эксцентрической модели (не будем забывать, что она эквивалентна эпициклической) этими параметрами являются: 1) среднее движение Солнца по кругу деферента, то есть вокруг его центра; и 2) эксцентриситет OT в долях отрезка OS, как показано на ил. 60. Нам необходимо получить угол ATS. Здесь O – центр деферента, а T – место наблюдателя на поверхности Земли, а ее размерами, как предполагается, можно пренебречь. Угол ATS получается как разность среднего движения (угол AOS) и угла OST. Угол AOS (среднее движение), очевидно, можно представить в виде табличной величины, зависящей от времени, измеряемого, например, в сутках или часах, или одновременно и в часах, и в сутках, поскольку оно течет равномерно. С помощью тригонометрических преобразований угол OST может быть довольно легко представлен в виде функции, зависящей от среднего движения и эксцентриситета. (Птолемей называл этот угол простафарезис – «угол, который должен быть прибавлен, либо вычтен»; мы же будем называть его уравнением или аномалией. Смысл заключается в том, что он позволяет внести поправку для среднего положения и получить из него истинное, где под «истинным» понимается видимое нами на самом деле.) Таким образом, Птолемей составил таблицу, позволяющую совершить быстрый переход к истинному положению, исходя из среднего движения, которое, в свою очередь, определялось из первой таблицы.

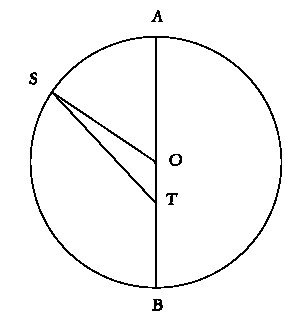
60

Модель движения Солнца, в которой используется простой эксцентрический круг. Предполагается, что Солнце движется по нему с постоянной скоростью (то есть угловая скорость вращения Солнца вокруг центра круга не меняется).

Здесь, вероятно, нужно особо подчеркнуть: когда античные астрономы говорили о «среднем движении», они имели в виду угол, например угол перемещения за сутки или за час. Они могли также соотносить его с углом, накапливающимся в течение долгого периода времени, или с положением, достигаемым в результате этого движения. Конечно, мы тоже можем характеризовать угол, покрываемый за данную единицу времени, как движение, но они рассматривали этот вопрос иначе, чем мы, и у них не было нашего представления о мгновенной скорости.

Остается ввести еще один параметр, если, конечно, Птолемей действительно желал снабдить нас средством, позволяющим определять точное положение Солнца. Нужно знать день, когда оно проходит через некоторую исходную точку – апогей или перигей; или же, как вариант, можно использовать его положение в любой другой заданный день. Птолемей выбрал в качестве начала отсчета эпохальную дату – день, когда царем Вавилонии стал Набонасар. Это случилось 26 февраля 747 г. до н. э. Можно по-разному относиться к выбору столь ранней даты; в частности, это означало то, что ему не нужно было вводить обратный отсчет лет, то есть отрицательные годы.

Если бы Птолемей обладал более точными данными, он мог бы ввести еще один параметр, учитывающий движение линии симметрии AB. (Это – линия апсид, соединяющая апогей с перигеем.) Он был искренне убежден в равенстве продолжительности сезонов в его эпоху и во времена Гиппарха, и поэтому полагал, что линия апсид неподвижна.

С присущей ему проницательностью он не упустил то, что мы называем уравнением времени. В течение большей части истории ежедневное движение Солнца по небу использовалось для измерения коротких интервалов времени. Однако это движение является нерегулярным в силу двух причин. Существует годовое изменение скорости движения Солнца по эклиптике, объясняемое с помощью эксцентрической модели; однако неравномерность движения вокруг полюсов (движения, измеряемого относительно экватора) вызывается иной причиной – Солнце движется в плоскости (плоскости эклиптики), которая наклонена к экватору под углом более 23°. Птолемей разъяснил, каким образом можно компенсировать оба эти фактора. По сей день лучшие солнечные часы снабжаются сопроводительной таблицей, позволяющей учесть уравнение времени, и эта поправка – прямое наследие Птолемея.

ПТОЛЕМЕЕВА ТЕОРИЯ ДВИЖЕНИЯ ЛУНЫ

Четвертая книга «Альмагеста» содержит подробное обсуждение лунной теории Гиппарха в категориях модели концентрического деферента с новыми параметрами, полученными из наблюдений. В пятой книге, где он переходит к ее сравнению с собственными наблюдениями, Птолемей обнаруживает, что она хорошо работает только тогда, когда Солнце, Земля и Луна находятся на одной линии (в соединении и в оппозиции, или, если называть это одним словом – в сизигиях). Это и не удивительно, если принять во внимание тот факт, что затмения всегда были наиважнейшим фактором в установлении деталей исходной простой модели. Под прямыми углами к этим точкам (в «квадратурах») ошибка достигала нескольких лунных диаметров – отнюдь не самая удовлетворительная ситуация. Здесь Птолемей находит еще одну разновидность движения Луны, известную сегодня как эвекция, и ее открытие можно считать выдающимся достижением, хотя способ ее объяснения, предложенный Птолемеем, оказался не менее замечателен.

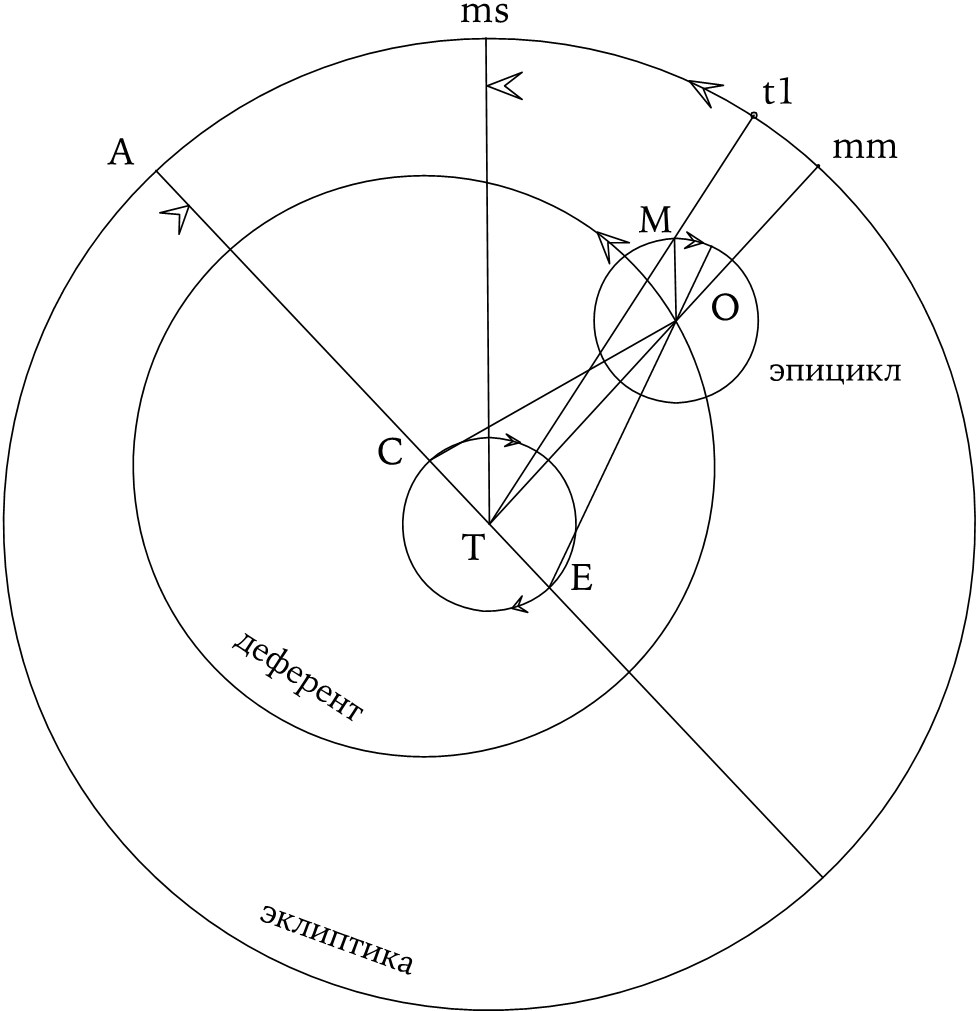
61

Лунная модель Птолемея. Точка T обозначает Землю, C – (подвижный) центр круга деферента, M – Луну, а E – точку «экванта», вокруг которой центр эпицикла (O) движется с постоянной угловой скоростью. Следует обратить внимание на нетипичное направление кругового вращения Луны в эпицикле. Эпициклам всех планет свойственно «прямое» движение, то есть вращение в противоположном направлении. Среднее эклиптическое положение Луны задается направлением mm, а окончательная истинная долгота – направлением tl.

Подробное изложение его доводов заняло бы слишком много времени, но можно кратко объяснить полученную им итоговую модель. Как и Гиппарх, Птолемей полагал, что Луна должна совершать попятное движение в эпицикле, но, в отличие от Гиппарха, он поместил центр деферента в точку C (как показано на ил. 61), эксцентричную по отношению к Земле и, в свою очередь, движущуюся по малому кругу вокруг Земли, находящейся в точке T. Затем ему понадобилось подобрать скорости, удовлетворительным образом приближавшие бы эпицикл к Земле, когда он находится в квадратуре по отношению к Солнцу. Он сделал это, проведя прямую в направлении среднего Солнца (ms), которая является биссектрисой угла между TO и TC. Следующее уточнение заключалось в том, что он стал вести отсчет постоянно растущего угла в эпицикле не от линии TO, а от линии EO. Это было равнозначно введению еще одной (третьей) вариации. Этим и отличался гений Птолемея – умением добавлять новые параметры к старой модели таким образом, чтобы удовлетворить требуемым условиям. Те, кто хорошо знаком с греческой одержимостью круговым движением, должны оценить методы, посредством которых Птолемей находил возможность преодолеть налагаемые ею ограничения.

Эта модель позволяла получать вполне приемлемые решения для долготы Луны, оказавшиеся лучше, чем все предыдущие. Эклиптика изображена на рисунке для того, чтобы показать, каким образом меняются ключевые долготы. Здесь mm обозначает среднюю Луну, A – движущийся апогей деферента, а tl – итоговую истинную долготу Луны. Однако описанная модель в том виде, как она здесь представлена, содержала один очевидный недостаток: слишком сильное изменение расстояния от Земли до Луны (M), вследствие чего за один полный оборот ее видимый диаметр должен был изменяться в размерах чуть ли не в два раза. Для понимания ошибочности этого не нужно быть астрономом, так как изменения размеров лунного диска на самом деле относительно невелики. Птолемей ничего не говорит об этом. Он достаточно хорошо объяснил изменение долготы, и, кроме того, расположив деферент и эпицикл в плоскости, наклоненной к плоскости эклиптики под углом 5°, он дал хорошее объяснение изменению широты Луны.

Существует распространенное убеждение: он не рассматривал свою модель как нечто, имеющее отношение к описанию реального перемещения тел в пространстве, и она стала не более чем средством расчета координат, и поэтому его не заботили прогнозируемые изменения размеров лунного диска. Однако из работы «Планетные гипотезы» мы узнаем, что Птолемея глубоко беспокоили вопросы, связанные с сотворением планетной системы, содержащей в себе весь сложный эпициклический аппарат небесных тел, в котором не должно было быть пустого пространства. Если он обратил внимание на прогнозируемые изменения размеров Луны, что предполагалось в его модели, – а не заметить этого он просто не мог, – то это непременно послужило для него причиной сильного разочарования.

Пятая книга «Альмагеста» заканчивается обсуждением вопроса о расстояниях до Солнца и Луны и содержит самое раннее подробное теоретическое рассуждение о параллаксе, то есть о поправках, которые необходимо вносить в видимое положение Луны, чтобы получить ее положение относительно центра Земли. (По поводу определения параллакса и открытий Гиппарха в этой области см. с. 157 и ил. 56 и 57. Радиус Земли составляет значительную часть расстояния до Луны. Полученное Птолемеем расстояние до Солнца, выраженное в диаметрах Земли, было сильно занижено – примерно в 20 раз.) Это дало ему возможность перейти к геометрическому описанию затмений. Он начинает с уже теоретически объясненных движений Солнца и Луны и не просто выводит из них обстоятельства, приводящие к затмению, но надеется получить закон их повторения. Птолемею посчастливилось воспользоваться вавилонскими наблюдениями затмений, начиная с эпохи правления Набонасара в 747 г. до н. э. У него не получилось очертить географические границы, в пределах которых возможно наблюдать солнечное затмение. Никто не мог справиться с этой сложной задачей, пока Кассини не занялся ею основательно в середине XVII в. Математические способности Птолемея вполне соответствовали уровню задачи, но у него не было доступа к широкому астрономическому сообществу, которое могло бы стимулировать его для дальнейшего рассмотрения этого вопроса.

НЕПОДВИЖНЫЕ ЗВЕЗДЫ У ПТОЛЕМЕЯ

Перед тем как заняться планетами, Птолемей обращается к долготам, широтам и величинам звезд. Он разделяет величины на шесть классов по признаку мегетос, более точным переводом которого является «размер», а не «блеск» (технический термин «величина», похоже, постепенно поменял свое значение с первого на второе только в XVIII в.). Согласно Птолемею, звезды шестой величины – это те, что едва различимы на небе, и сегодня мы, вообще говоря, продолжаем использовать эту классификацию, хотя и отвергаем его предположение о ее связи с размерами звезд. Каталог Птолемея из 1022 звезд в составе 48 созвездий и нескольких туманностей лег в основу почти всех последующих авторитетных каталогов в исламском и западном мирах вплоть до XVII в. Он был в значительной степени основан на данных, полученных Гиппархом, которые не дошли до нас, и, безусловно, учитывал его теорию прецессии – «движение восьмой сферы». Если Гиппарх попросту указал ее нижний предел, равный одному градусу за столетие, то Птолемей получил ее точное значение. Он не мог, как часто утверждается, получить свой каталог, просто прибавляя прецессию к координатам звезд из аналогичного каталога Гиппарха, поскольку данные, оставленные его предшественниками, записаны совсем в другой форме – с качественными описаниями, перечислением звезд, находящихся на одной линии, звезд, восходящих в одно и то же время, и т. д. Каталог Птолемея, повторим, являл собой удивительно искусно исполненный шедевр, даже если принять во внимание, что указанные в нем долготы звезд занижены.

Причиной этого весьма несущественного недостатка была высокая степень взаимозависимости между, на первый взгляд, совершенно разными частями книги Птолемея. Он часто определял долготы звезд, соотнося их с Луной, но ошибка в определении движения Солнца, которое, как мы недавно убедились, предваряло введение лунной модели, слегка исказила данные его измерений. Большинство из тех, кому в последующие столетия требовалось знать точные положения звезд, ограничивались прибавлением прецессии к долготам из его каталога, и это позволило ему сохраниться до наших дней. Лучшие астрономы включали в него результаты собственных измерений, но основательность Птолемея долгое время оставалась непревзойденной.

ПТОЛЕМЕЙ О ПЛАНЕТАХ

В девятой, десятой и одиннадцатой книгах «Альмагеста» объясняется, каким образом можно рассчитать долготы планет – нижних (Меркурия и Венеры) и верхних (Марс, Юпитер и Сатурн). Как мы показали в главе 3, для этого нужно использовать две разных схемы расположения эклиптики по отношению к деференту, и поскольку Меркурий вызывает определенные, присущие только ему трудности, то для этой планеты требовалось ввести дополнительные уточнения. Здесь мы снова приведем только итоговые результаты работы Птолемея. В данном случае он располагал гораздо меньшим количеством надежных данных, полученных от предшественников, чем в случае Солнца и Луны. В его распоряжении были, конечно, концепция эпицикла и – через посредство Гиппарха – некоторые вавилонские периодические соотношения, типа «за 59 лет Сатурн дважды возвращается на исходную долготу и 57 раз – в исходную аномалию (эквивалентную точке стояния в начале попятного движения)». Эти периодические соотношения дали ему возможность построить таблицы средних движений, хотя впоследствии ему понадобилось подкорректировать их с учетом выработанных им моделей.

Вероятно, здесь уместно будет добавить, что Птолемей указал два различных подхода, позволяющих очень точно определять средние планетные движения. В дополнение к упомянутому здесь пояснению он отметил далее возможность их получения напрямую из наблюдений в течение продолжительного времени. В принципе, они могли бы быть найдены таким способом, однако, как легко показать, это вряд ли можно было осуществить на практике. Что касается согласования параметров, полученных им из периодических соотношений, то в отдельных случаях это сделано на основе производимых им наблюдений, однако в случае Меркурия и Сатурна наблюдения, на которые он ссылается, не соответствовали выведенным из них, по его утверждению, средним движениям.