
Полная версия
Los problemas de matemática en la práctica didáctica
card (X U Y) = card X + card Y
cuáles que sean los conjuntos X y Y con X∩Y=∅.
Es claro que la toma de conciencia de tales teoremas en acto constituye una formación genuina de conceptos y que la situación más natural para hacer emerger tales teoremas en acto es la resolución de problemas (mejor si son concretos).
Por ende, se trata, entre otras cosas, de una manera activa y deductiva de ver la resolución de problemas.
Nota bibliográfica
Para la redacción de esta sección, he usado (Furth, Wachs, 1977; Petter, 1984; Vergnaud, 1981a, 1985a, 1990a, 1990b).
Para una crítica a la posición descrita por Piaget, ver (Donaldson, McGarrigle, 1974; Freudenthal, 1973; McGarrigle, Grieve, Hughes, 1978).
Para un estudio detallado y moderno sobre la diferencia entre ejercicio y problema y sobre el aprendizaje estratégico en un contexto teórico más amplio (Fandiño Pinilla, 2008).
1.3. Problem solving y problem posing
En este proceder a manera de espiral, encuentro la necesidad de contraponer dos problemáticas aparentemente opuestas, las del título de la sección.
Ya he hecho notar como uno de los impulsos para aprender es la motivación y la gratificación (placer ‘interno’, es decir satisfacción interna, o el reconocimiento social de ser considerado un buen solucionador de problemas). Por tanto, aparte de la motivación, la actividad de la resolución de problemas puede con razón ser considerada una extensión del aprendizaje de reglas o de maneras de comportarse o de obtención de ejemplos y estrategias, etc.
Tal proceso, difícil de definir, en su mayoría se desarrolla dentro del alumno que lo resuelve, aun cuando las sugerencias que llegan al sujeto que está resolviendo el problema sean notables (facilidades, sugerencias, etc.) bajo la forma de varios tipos de comunicación (verbal o no).
Por muy importante que sea la aplicación de reglas (normas, experiencias, […]) precedentes, vale la pena resaltar que el proceso resolutivo genera también y sobre todo un nuevo aprendizaje. Es cierto que, en primera instancia, aquel que resuelve intenta aplicar reglas (normas, experiencias, […]) precedentes (mejor aún si fueron exitosas); pero también es cierto que, si la situación problemática es oportuna, el sujeto podría no encontrar simplemente una solución análoga o idéntica a una precedente. En cambio, puede encontrar una combinación particular de reglas (normas, experiencias, […]) del todo nueva que enriquecerá el campo de la experiencia y a la cual se puede recurrir en el futuro. En fin, una frase en la que creo firmemente: resolviendo un problema, el sujeto aprende.
En este sentido, el modelo de referencia al que nos aferramos no tiene importancia, si es el de Dewey (1910) o en cambio el primero o el último de Gagné (1962, 1976); la cuestión es muy general y puede funcionar en todos los casos.
Por ahora, podemos llamar a esta serie de fragmentos “estrategias de resolución de problemas”:
• exploración de las reglas (normas, experiencias, [...]) ya conocidas y ya aplicadas;
• descarte de cada una;
• análisis de la situación desde varios puntos de vista;
• construcción de una regla completamente nueva, obtenida de la “dosificación” en manera oportuna de reglas (normas, experiencias, […]) usadas precedentemente;
• verificación de la capacidad de resolver el problema con la regla nueva.
Esta es la razón por la cual Gagné subraya la exigencia que «la expresión problem solving sea usada en general para referirse a problemas nuevos» (nosotros diremos: a verdaderos problemas y no a ejercicios). Él ejemplifica, entre estos, los siguientes: parquear el carro en un lugar permitido y cercano al lugar de trabajo; entender por qué suceden las fases lunares; describir un comportamiento indolente mediante las acciones de un personaje; (…) El hecho que la resolución induzca al pensamiento nos hace hablar de problem solving productivo (precisamente porque se produce un efecto).
Finalizados estos ejemplos, por así decirlo, de la vida real, Gagné (1976) pasa a problemas más cercanos a la praxis escolar, explicando bien la diferencia que hemos indicado mediante la dicotomía problema/ejercicio, pero lo ejemplifica también mediante juegos de cambios de lugar de fósforos, lo que ha sido analizado en modo particular desde un punto de vista psicológico por George Katona (1967). En este estudio, Katona sugiere una sucesión de métodos usados para hacer que los sujetos resuelvan problemas-juego con fósforos:
• hacer los movimientos precisos frente a los ojos del sujeto examinado, haciendo que este último recuerde los movimientos exactos;
• exponer verbalmente las propiedades “matemáticas” de los fósforos en cuestión, notando cómo los fósforos con “funciones” dobles deben ser movidos para tener una función “simple” o haciendo desaparecer por completo las figuras para hacer reconstruir la estructura deseada, con los vínculos deseados;
• proceder al descubrimiento guiado (ésta es la denominación usada): sin enunciar las reglas, proceder paso a paso, ilustrando los cambios producidos, dejando vacíos en la figura original.
Esta sucesión no es casual; según Katona el primer método lleva a un aumento banal de las capacidades; el segundo es mucho mejor; pero solo el tercero, en el cual el sujeto mismo descubre la regla, lleva a poseer satisfactoriamente la competencia. La enunciación verbal de la regla, que sin dudas produce efectos positivos, ayuda a muchos sujetos, pero no a otros. Haber descubierto por sí mismo la regla a aplicar, aún en contextos limitados, produce conocimientos y competencias en todos. Gagné (1973) ilustra otros ejemplos, además de aquel de Katona, entre los que se encuentra el experimento del péndulo de N. R. F. Maier, el cual describiré en breve.
Los resultados de tales experimentos se pueden condensar de la siguiente manera: se produce un efecto positivo en el sujeto que resuelve si se dice exactamente la naturaleza de la actuación (performance) que de él se espera; incluso si no se hace explícitamente, se puede dar una guía en cuanto a la elección de reglas (normas, experiencias, […]) que son útiles para escoger la estrategia, mediante la formulación del problema.
Toda la actividad y la atención del problem solving radican en la resolución.
De otra naturaleza, pero siempre dentro de la misma problemática, es la actividad del problem posing. Esta actividad involucra dos maneras diferentes, pero estrechamente interconectadas, de actuar:
• la creación de un problema basado en la reflexión relativa a un tema de examen;
• la propuesta de las preguntas que analizan situaciones “limítrofes” (externas pero cercanas) a un problema de examen.
Los autores del texto que volvió famoso el problem posing, S. I. Brown y M. I. Walter (1988), distinguen dos modos de actuar diferentes:
• hacer o hacerse preguntas
• preguntarse siempre «¿Y si (...) ?», o «¿Y si no (...) ?»
lo cual da muy buena cuenta de la cuestión.
Una reducción didáctica trivial del problem posing es la actividad consistente en hacer que los alumnos inventen los problemas: ésta ha sido ampliamente estudiada en la investigación en Didáctica de la Matemática y tendremos ocasión de entrar en detalles. Pero el problem posing, en su formulación más general y genuina, debe llevar a nuevos problemas, si bien generados a partir de aquellos presentes en situaciones anteriores. Este tipo de actividad lleva a generar un descubrimiento y en este sentido, a mi modo de ver, se asemeja mucho al que los estudiosos del problem solving han resaltado.
Dado que tendré que retomar este argumento en la siguiente sección, me limitaré a presentar este boceto a manera de resumen.
Experimento del péndulo de Maier del 1930, (Gagné, 1973).
El sujeto examinado es conducido a una habitación de 5 m por 6 m aproximadamente, en la que hay una mesa de trabajo. El sujeto tiene a su disposición tablillas, pedazos de hilo, tiza y abrazaderas. El problema es descrito en estos términos: construya dos péndulos, de manera que cada uno, oscilando y teniendo en cada extremidad una tiza, marque un punto establecido sobre el piso.
Para ilustrar mejor el problema, he aquí la representación de una buena solución proporcionada por sujetos sometidos a la prueba.

Con algunos sujetos, Maier usó la estrategia de recordar problemas precedentes que, en este caso, son, por decirlo así, sub problemas:
• cómo se hace una plomada, teniendo a disposición hilo, abrazaderas y tiza;
• cómo hacer un poste largo, teniendo a disposición dos postes cortos y una abrazadera;
• cómo anclar al techo un objeto prensado entre dos postes.
Maier hizo sugerencias sobre la resolución presentando otro problema: el problema sería más simple si existiese una puntilla y se pudiera clavar un poste al techo. El experimento de Maier mostró cómo las instrucciones adicionales, que permiten recordar soluciones parciales precedentes, llevaron a los sujetos a la resolución del problema con mayor frecuencia, en comparación con aquellos que escuchaban solo el enunciado del problema sin ayudas adicionales. La sugerencia sobre la puntilla (que Maier llamó “dirección”), favorecía más la probabilidad de resolución.
Nota bibliográfica
Para la redacción de esta sección, utilicé (Dewey, 1910; Aebli, 1961; Katona, 1967; Gagné, 1973; Brown, Walter, 1988).
1.4. Problem solving, problem posing y descubrimiento
Empezamos con un ejemplo:
Dados dos triángulos equiláteros, encuentre un tercero, cuya área sea igual a la adición de las áreas de los otros dos. (Tomado de: Brown, Walter, 1988, p. 157).
Dentro del espíritu del problem posing, en cada intento por resolver el problema propuesto se cumple un análisis preliminar. Cada alumno tiene su propia reacción. Se puede notar que faltan datos y por lo tanto preguntar cuál es la naturaleza de la pregunta; ¿Cuál(es) de la(s) propiedad(es) de los triángulos entra(n) en juego?, ¿se espera una solución geométrica (un dibujo), o una numérica? Es claro que cada solucionador puede escoger la estrategia más adecuada de acuerdo con su propio “estilo”. Por ejemplo, un alumno puede decidir que va a estudiar un caso particular con los triángulos dados, uno de lado 3 y el otro de lado 7 y proceder de tal manera, haciendo un dibujo y recortando pedazos de cartulina (el cálculo sugerido por los autores no es, ciertamente, adecuado para niños de escuela primaria, pero quiero resaltar un espíritu independiente de estas contingencias) o usando un software geométrico a este propósito. Sin embargo, pero, aunque se haya encontrado una solución (aproximada), ¿qué sucede si se cambian los datos inventados, 3 y 7?
Lo que quiero subrayar aquí es que el problem posing es una forma de ubicarse dentro del problem solving y que, por ende, las dos problemáticas no son opuestas, sino bastante cercanas. “Plantear un problema” es solo una manera de comprenderlo mejor, de analizarlo mejor; hacerse preguntas que parecerían (…) rebotar la solicitud, puede significar entrar en mayor confianza con el problema.
Por tanto, si se llega a la resolución del problema, el problem posing tiene un efecto a posteriori, porque las preguntas sobre el problema y sobre la solución proporcionada no cesan: ¿se podría hacer de otra manera?, ¿se podría usar otro dato?, ¿hay una manera general de resolver esta cuestión?, ¿alguien ha inventado este método?, ¿cuándo y por qué se planteó este problema? (…) En una situación simétrica se plantea el efecto a priori que es sustancialmente el análisis de todos los detalles del problema antes de proceder con la solución.
En definitiva, el problem posing se ubica dentro de la amplia problemática del problem solving y no se limita a ser simplemente interpretado como un “hacer que los niños inventen problemas”, actividad que, entre otras cosas, es significativa si se conduce de manera motivada y prudente.
A mi modo de ver, dentro de los ejemplos dados por los Autores citados, es pertinente hablar del célebre caso del niño Gauss, muy famoso en las escuelas italianas:
Calcular la suma de los números naturales de 1 a 100.
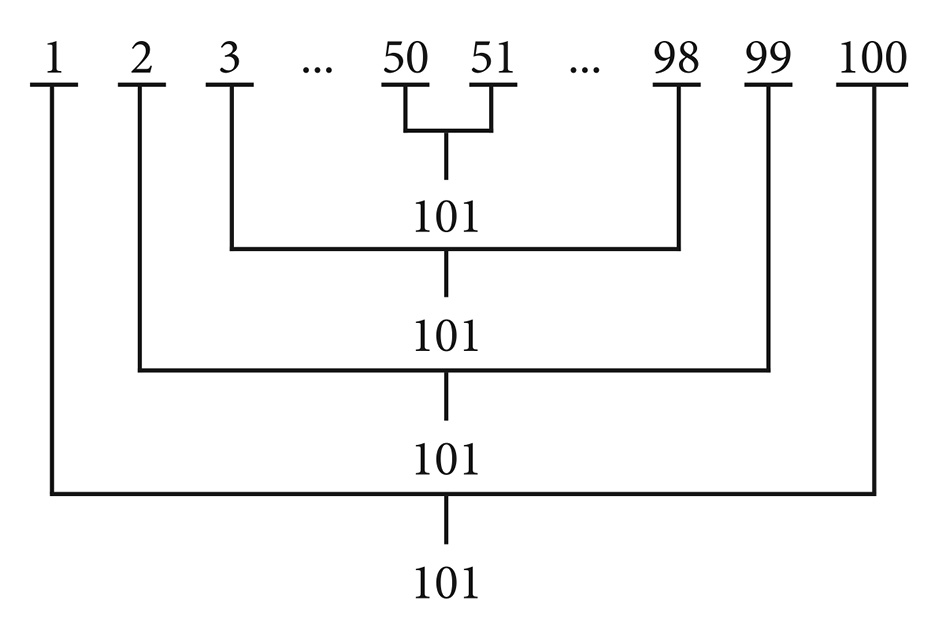
Es bien sabido que el procedimiento usado por Gauss es el siguiente: se observa que 1+100=101, 2+99=101, 3+98=101, y así hasta la última adición 50+51=101. Por lo tanto, la suma buscada se puede expresar como 50 veces 101. Éste es un buen ejemplo del problem solving que utiliza una manera de entender el problem posing, según lo que se ha dicho antes. En cambio de hacer lo que parece sugerir el texto del problema (es decir una secuencia absurda de cálculos 1+2=3, 3+3=4, 4+4=8, 8+5=13, haciendo 99 adiciones), analizamos el problema con “y si (...)”: «Y si en lugar de adicionar en orden, sumo el primero y el último, ¿qué encuentro?».
Entonces: se descubre una regularidad.
Se obtiene una regularidad adicionando en escala ascendente/descendente: hemos descubierto una regla («Una trampa» como dicen los niños). Pero para hablar de una regla, o de un descubrimiento, y proporcionarle dignidad en el mundo de la Matemática, es preciso que ésta sea general: ¿es siempre válida?, ¿si en lugar de 100 fuera 167?, ¿si en lugar de 1 partiéramos de 34?, ¿si en lugar de un número par tuviéramos un número impar? Y así sucesivamente.
Con base en las preguntas planteadas, hay una actitud analítica (llamémosla fantasía o curiosidad activas) que necesariamente hace que la resolución sea un descubrimiento.
El problem solving como método de aprendizaje exige que el sujeto descubra una regla de orden superior sin ayuda específica. Presumiblemente, el sujeto construye una nueva regla a su manera, aunque no esté en capacidad de comunicarla después de haberla descubierto. Ver específicamente Gagné (1973, p. 268). Este autor, haciendo referencia a los experimentos de Worthen, afirma que el método del descubrimiento (descrito anteriormente) lleva a un transfer amplio de las reglas adquiridas.
También en este caso, es importante señalar cómo la idea de la didáctica del descubrimiento se ha desacreditado en la práctica didáctica.
Las pruebas sobre el uso de los descubrimientos en el problem solving proporcionadas por los experimentos han ciertamente demostrado que las reglas de orden superior deben ser obtenidas mediante el descubrimiento. Muchas veces, por ejemplo, en el aprendizaje de los adultos, una guía llena de descripciones verbales puede ser tan completa que la regla a ser aprendida se enuncia verbalmente durante el proceso mismo de aprendizaje. La clave de la adquisición de una regla de orden superior no radica solamente en el método del descubrimiento. No obstante, la evidencia sugiere fuertemente que la adquisición de una regla de orden superior mediante el problem solving produce una capacidad muy eficiente, que permanece durante un período de tiempo importante. (Ver específicamente Gagné, 1973, p. 269; aquí Gagné cita estudios de Worthen, Shulman y Keislar, Ausubel, Gagné y Bessler, Guthrie, que no retomo en su totalidad).
Por lo tanto, se ve el problem posing como elemento determinante del proceso del problem solving y de preludio al descubrimiento.
Sin embargo, me parece honesto y necesario señalar que el problem solving no puede ser siempre exitoso. Por ejemplo, si las reglas a encontrar son de una complejidad superior a aquella a la cual puede llegar el sujeto, no se podrá tener más que una solución parcial (en casos particulares). Pero sobre este tema regresaré más delante.
Nota bibliográfica
Para la redacción de esta sección, hice uso de (Brown, Walter, 1988; Gagné, 1973).
Sobre el transfer, ver (Barth, 1990; Roveda, 1979).
1.5. Tipos de aprendizaje
Ya que resolver problemas es aprender, no resulta inútil, en este ámbito, analizar los diferentes tipos de aprendizaje; muchos estudiosos han buscado clasificaciones a propósito de este tema: entre las cuales se encuentra la afortunada descripción de Gagné (1973), expuesta brevemente en esta sección.
Hay que decir, para evitar problemas, que el Gagné al quien me refiero en estos primeros capítulos, es aquel que publicó ediciones sucesivas desde 1970 (hasta la tercera en 1977) de su exitoso libro The Conditions of Learning, cuya primera edición apareció en 1965. Una sucesiva edición del mismo libro salió en 1985, con el mismo título, con una nueva editorial: Holt, Rinehart and Winston Inc. a Cbs College Publishing. El éxito de la primera versión del libro fue tal que aún hoy Gagné es recordado por su vieja posición, la cual presentaré en estos primeros capítulos. La utilizo como base, como trampolín, para poco a poco alejarme de ella de manera crítica. Por otro lado, es de resaltar que anteriormente hice referencia al Gagné más reciente (en la sección 1.3.).
• I tipo: aprendizaje de señales. Se trata del aprendizaje a través de un estímulo que produce efectos, repetido más de una vez; a tal punto que, aunque el estímulo no produzca más el efecto, se obtiene una respuesta. Se trata de la díada estímulo/respuesta, ampliamente estudiada por parte de los psicólogos, entre los cuales se destaca ciertamente el nombre de Pavlov. Hay que subrayar que las respuestas voluntarias no pueden ser aprendidas de esta manera.
• II tipo: aprendizaje estímulo/respuesta. Es la especialización del tipo precedente, típica tanto en el aprendizaje animal como en el humano. Se distingue del primer tipo por el resultado. La respuesta del sujeto, en este caso, es un acto preciso y delimitado, mientras que en el primer tipo se trata de una respuesta genérica y emotiva. Por ejemplo, el perro se entrena para “dar la pata” con la repetición de los siguientes dos estímulos: se le dice «¡Da la pata!» mientras, contemporáneamente, se le levanta la pata con la mano, reforzando el gesto con cumplidos, caricias o premios. Ferster y Skinner al final de los años 50 estudiaron precisamente este ejemplo con lujo de detalles. Si con S → R se indica el proceso estímulo/respuesta del tipo I, se propone usar Ss → R para indicar el tipo II, donde el símbolo Ss es el estímulo externo sumado al interno (propiocepción). La capacidad conseguida ha sido largamente estudiada por Skinner (experimentos sobre el aprendizaje de ratones en laberintos) y también ha sido propuesta para explicar varios aprendizajes en niños muy pequeños, por ejemplo, el aprendizaje de palabras. (Pero existen varias reservas al respecto).
• III tipo: concatenación. Se trata de una multiplicidad de aprendizajes del II tipo concatenados entre sí. Por ejemplo, a un perro se le puede enseñar primero a dar la pata a quien se lo pide e inmediatamente después a ladrar, como señal de saludo. Este tipo de aprendizaje fue estudiado ampliamente para tratar de comprender los procesos evolutivos en niños pequeños. Lo que se sugiere es que cada uno de los “eslabones” de la “cadena” debe ser estable (es decir cada Ss debe llevar su R de manera sólida) y que debe haber “continuidad” entre cada uno de los eslabones (en términos esencialmente, pero no solamente, de tiempo). Entonces, asegura Gagné, «cuando las dos condiciones precedentes se ven plenamente satisfechas, resulta que la adquisición de una cadena no es un proceso gradual, sino que sucede en un solo momento».
• IV tipo: asociación verbal. Se trata de una subespecie del tipo anterior, en la que la respuesta R es una palabra. Por ejemplo, se le muestra un fósforo a un niño diciéndole el nombre más de una vez (un caso particular es el del uso de una lengua que no sea la propia, la materna, del sujeto que aprende, por ejemplo, otro idioma). Esto parece estimular un espacio de “conexión codificante” (que luego se vuelve automática) en el sujeto. Según varios investigadores es precisamente en el IV tipo en el que se activa un mecanismo típicamente humano; mientras los tres tipos anteriores son procesos de aprendizaje que podrían resultar exitosos tanto para animales como para seres humanos, el cuarto tipo constituye una restricción.
• V tipo: aprendizaje de distinciones. Los aprendizajes de tipo II, aun siendo parte de una concatenación, son hechos aislados. Se trata, por lo tanto, de aprendizajes “simples”. Sin embargo, precisamente por este motivo, así como son fáciles de almacenar también son fáciles de olvidar (“sofocados”, por ejemplo, por otra actividad). Si alguien es sometido al aprendizaje de muchos ejemplos de tipo II, o de varias concatenaciones de tipo III, es fácil que se olvide de todo o se confunda. No obstante, se activa un aprendizaje diferente, llamado “por distinción”. Se trata de “vincular” objetos (o nombres) aprendidos mediante relaciones debidas a invenciones o estilos personales, que no siempre se pueden codificar o hacer explícitas. Esto parece permitir la interferencia entre diferentes concatenaciones, lo cual parece ser la causa principal por la cual se olvida lo aprendido. En este punto, aparece una discusión frecuentemente escuchada por los psicólogos: ¿La distinción puede ser un hecho “mecánico”? Dicho de otra forma, se puede aprender sin olvidar, si voluntariamente se asocia a cada concatenación una relación explícita entre objetos (o nombres) para hacer que el recuerdo sea más fácil. El estudio de esta cuestión (procesos de memorización) ha puesto el acento sobre otro tema que pasaré por alto: ¿Qué quiere decir “mecánico” en este ámbito?
• VI tipo: aprendizaje de conceptos. Hasta ahora hemos aprendido a hacer ciertos movimientos, a reconocer los objetos nominados, a dar nombres nuevos a objetos conocidos; pero lo que nos interesa es el aprendizaje de algo más elevado: los conceptos. Este tipo de aprendizaje está fuertemente relacionado con la capacidad de “representación interna”, es decir la capacidad de manipular simbólicamente el ambiente externo, sin intervenir en éste físicamente, simplemente imaginando tal manipulación. Un ejemplo banal: imaginar lo que le sucedería al ambiente en el que me encuentro (mi estudio, en Bogotá, en el que escribo rodeado de 10000 libros) si un espíritu maligno cortara asimétricamente las bases de las bibliotecas. Concretamente, no sucederá jamás (¡eso espero!) pero puedo muy bien imaginar las consecuencias. Ahora bien, parece que algunos primates superiores tienen destellos de este tipo de capacidad, pero es seguro que la consciencia y madurez plena de esto reside sólo en el complejo mecanismo del cerebro humano. Aprender un concepto significa aprender a clasificar las situaciones estimulantes en términos de propiedades abstractas como colores, formas, posiciones, números y similares. Por ejemplo, la generalización que hace un niño, incluso en edad preescolar, al llamar “cubo” o “dado” a tal forma independientemente de su dimensión, color o peso, pertenece a este tipo de aprendizaje. La definición matemática del cubo, con términos precisos, aunque pertenecientes al lenguaje común, no ayuda en el acto del aprendizaje puro; en el caso del aprendizaje se trata de un acto interno, intuitivo e interior. Me parece aún más estimulante el estudio psicológico de la manera como se da el aprendizaje de tipo abstracto; por ejemplo, el aprendizaje de lo que significa “estar en medio”, cuando no solo cambian las propiedades de los objetos (como en el caso de cubos diferentes), sino que cambian también los objetos mismos. Aquí y en los casos análogos resulta esencial la variedad de los estímulos, aún más si a este aprendizaje se asocia, como sucede muy frecuentemente, el uso de una terminología nueva. Un adulto, dada su vasta experiencia lingüística, supera la falta de información circunstancial (relativa al caso específico) haciendo uso de conocimientos análogos; sin embargo, este tipo de aprendizaje en el niño resulta sorprendente. Tanto es así que un adulto puede aprender fácilmente conceptos abstractos solo basándose en definiciones verbales, esto en cambio no puede suceder en un niño pequeño con poca experiencia en el uso del lenguaje.




