Психология интеллекта и одаренности

Рис. 1.1. Вверху – схема отношений способностей и компетентностей. Внизу – диаграмма рассеяния интеллекта школьников с их результатами решения олимпиадных математических задач

В условиях примерного равенства внешних возможностей реализация потенциала способностей и превращения их в компетентности оказывается в зависимости от психологических факторов, таких как мотивация, эмоциональная и волевая сфера и т. д. Собственно, основное, что может сделать образование одаренных детей для экономики страны – более эффективно помочь преобразовать их способности в высокие компетентности.

Компетентность и экономическая эффективность

Рассмотрим теперь превращение компетентностей в экономический результат. Проводя дальше линию анализа экономики как решения задач по аналогии с открытыми и закрытыми задачами, введем различение профессиональных деятельностей с открытым и закрытым типом успешности. Задачи закрытого типа предполагают только один вариант решения, который является оптимальным и не может быть дальше усовершенствован. Задачи открытого типа имеют множество решений, степень совершенства которых сверху не ограничена.

Если обратиться к миру профессий, то очевидно, что, например, деятельность рабочего у конвейера, контролера в общественном транспорте или кассира имеет закрытый тип успешности. При низком уровне компетентности эта деятельность не достигает оптимума успешности и характеризуется большим количеством брака. Однако по достижении определенного уровня компетентности успешность достигает потолка и далее не возрастает.

Профессии закрытого типа успешности могут быть весьма разными по когнитивной сложности и требовать разных уровней компетентности и необходимой для ее приобретения способности. Если работа у конвейера обычно не рассматривается как требующая интеллекта выше среднего, то деятельность, например, нотариуса, согласно американским правилам профессионального отбора, предполагает интеллект, превышающий средние значения более чем на одно стандартное отклонение (Gottfredson, 1997). Тем не менее нотариус или же бухгалтер – тоже профессии с закрытым типом успешности: после достижения определенного уровня профессиональной компетентности прирост успешности прекращается. Суть этих профессий – проведение действий в соответствии с установленными нормами. Если нормы выполняются, деятельность должна быть признана успешной, и далее ее успешность не повышается ввиду того, что превышать нормы не требуется или даже противопоказано.

В то же время вроде бы близкая деятельность адвоката не имеет четкого потолка успешности. Возможность влиять на суд в пользу своих подзащитных выдвигает из среды адвокатов таких выдающихся личностей, как Плевако или Кони. Аналогично, например, в сфере науки продуктивность ученого не ограничена сверху, и вклад талантливых личностей в ее развитие многократно превосходит среднестатистический уровень. Только что обсужденный аспект модели имеет любопытные следствия. Если способности нормально распределены в соответствии с гауссовым законом, то треугольный характер зависимости, представленной на рисунке 1.1, будет приводить к возникновению левосторонней асимметрии распределения компетентностей, как это показано на рисунке 1.2 (см.: Дружинин, 2002).

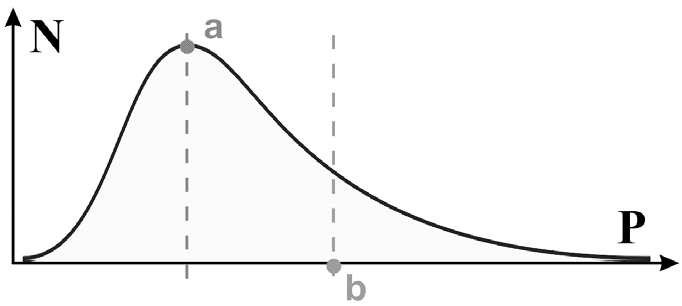
Рис. 1.2. Левосторонняя асимметрия распределения компетентностей

Если сопоставить асимметрию распределения компетентностей, изображенную на этом рисунке, и соотношение компетентностей и достижений в профессиональной деятельности открытого типа успешности, можно придти к выводу, что в наиболее творческих профессиях следует ожидать резкую асимметрию распределения достижений. Это означает, что в таких профессиях значительную часть продукта производит относительно небольшая часть занятых в них людей. Собственно, это совпадает с эмпирически установленными закономерностями.

Еще в конце XIX в. социолог Парето установил, что 80 % доходов в Англии того времени получали 20 % населения и нашел схожее распределение для других стран и времен. Хотя из асимметрии распределения трудовых вкладов и должна следовать асимметрия доходов, обратное неверно. Кроме того, распределение Парето оказалось применимым к очень широкому кругу феноменов – от функционирования компьютерных процессоров до систем контроля качества на производстве. В этом смысле его трактовка как следствия асимметрии трудовых вкладов представляется необоснованной, хотя применение принципа Парето к распределению трудовых вкладов на предприятиях может рассматриваться как достаточно правдоподобное.

Существуют, однако, другого рода оценки – связанные с закономерностями, которые были обнаружены в творческих профессиях. Так, согласно закону Прайса (Price, 1963), половина всех произведений в данной области создается группой, численность которой равна корню квадратному из общего числа членов данного сообщества. Например, если классический музыкальный репертуар образован произведениями примерно 250 композиторов, то половина этого репертуара принадлежит корню квадратному из 250, т. е. примерно 16 композиторам, что и обнаруживает эмпирическое исследование (Moles, 1968). Функция распределения продуктивности в любой сфере творчества оказывается резко асимметричной, причем асимметричность увеличивается с ростом выборки. Для разумных объемах выборки асимметрия оказывается существенно выше, чем в случае распределения Парето.

На основании изложенных положений модели можно выдвинуть следующее дополнительное предсказание: увеличение значимости наиболее сложных и творческих компонентов в деятельности будет приводить к нарастанию асимметрии. Это предсказание до сих пор не проверялось, однако допускает эмпирическую проверку. Например, можно предположить, что периоды «научных революций» в смысле Т. Куна требуют более неординарных подходов, чем периоды «нормального развития науки», и, следовательно, будут приводить к более выраженной левой асимметрии распределения научного продукта, в том числе измеряемого – публикаций.

Из сказанного вытекает объяснение большей асимметричности распределения Прайса, чем распределения Парето. Если распределение Парето можно рассматривать как описывающее распределение вкладов на средней корпорации, то распределение Прайса относится к «верхним этажам» человеческого творчества. Из излагаемой модели следует, что во втором случае асимметрия должна быть больше.

Оценка связи способностей, компетентности и экономических показателей в современном мире

Теперь следует перейти на более высокий уровень – от успешности деятельности отдельного профессионала к предприятию и экономике в целом. Прежде всего очевидно, что перед разными странами (и предприятиями) стоят разные задачи и для достижения одинаковых результатов от них требуются разные усилия и уровни компетентности. Следовательно, уровень компетентностей – лишь один из факторов, определяющих экономический успех, но, как будет видно из дальнейшего, весьма существенный фактор, объясняющий значительную часть дисперсии экономических показателей.

Показатели экономики представляют собой нелинейную комбинацию результатов профессиональной деятельности отдельных индивидов. Другими словами, общий результат экономики можно представить как входящие в него с разными весами результаты различных профессиональных деятельностей с закрытыми и открытыми типами успешности. В этом случае инновационная экономика характеризуется тем, что с наибольшим весом в нее входят профессиональные деятельности с открытым типом успешности.

Таким образом, связь между компетентностями людей и экономическими результатами оказывается опосредованной экономическим устройством общества. Эти процессы и структуры сами по себе представляют существенный интерес и заслуживают отдельного моделирования. Мы же здесь же воспользуемся существующими данными, которые позволяют установить отношение, характеризующее современную мировую экономику.

Для оценки связи способностей, компетентности и экономических показателей в современном мире сегодня есть возможность воспользоваться данными, собранными известным английским психологом Р. Линном.

Линн начинал с данных, касающихся связи экономического развития регионов различных стран с интеллектом их населения (см., например: Davenport, Remmers, 1950). Затем он получил аналогичные данные для различных регионов западноевропейских стран. Корреляции составили r = 0,73 для 13 областей Великобритании, r = 0,61 для 90 департаментов Франции и r = 0,65 для 48 районов Испании (Lynn, 1979, 1980, 1981).

В 2002 г. Линн и финский политолог Т. Ванханен выпустили книгу «Коэффициент интеллекта и благосостояние наций», в которой утверждалось, что интеллект населения стран является существенным фактором, оказывающим влияние на состояние их экономик (Lynn, Vanhanen, 2002). Авторы составили список среднего интеллекта для 81 страны мира на основании опубликованных данных исследований интеллекта (рисунок 1.3). Они обнаружили высокую корреляцию посчитанного ими национального интеллекта как с доходом на душу населения в этих странах (корреляция составила примерно 0,7), так и с экономическим ростом в периоды 1950–1990 и 1976–1998 гг. (корреляция 0,6–0,65). Эти корреляции лишь незначительно уменьшались, если из списка, например, выводились африканские страны.

Рис. 1.3. Связь национального интеллекта и среднедушевого дохода в различных странах мира

В более поздней работе на материале тех же данных Р. Дикерсон уточнил, что связь интеллекта с доходами страны аппроксимируется экспоненциальной зависимостью лучше, чем линейной (Dickerson, 2006). При повышении коэффициента интеллекта на 10 баллов национальный доход на душу населения примерно удваивается.

В соответствии с изложенной моделью связь между интеллектом и экономическими показателями опосредована компетентностями людей. Следовательно, если адекватно измерить в межгосударственном масштабе компетентности, можно ожидать, что их корреляции как с национальным интеллектом, так и с экономическими показателями окажутся выше, чем у этих двух конструктов между собой. Меры, позволяющие оценить компетентности, логично искать в сфере оценок образовательных систем. На первый взгляд данные, полученные в этой сфере, могут показаться довольно противоречивыми.

В работах экономистов с применением метода Байесовского усреднения классических оценок (BACE – Bayesian Averaging of Classical Estimates) было показано, что интеллект проявляет себя более мощным предиктором экономического развития, чем различные параметры системы образования (средняя продолжительность образования, его охват и т. д.), как, кстати, и рыночная свобода, демократия, инвестиции (Weede, Kampf, 2002; Jones, Schneider, 2006).

Иную картину, однако, дает анализ показателей образования не по формальным признакам, а по результатам испытаний учащихся.

С одной стороны, Линн показал высокую связь показателей среднего интеллекта по странам и результатов международных исследований качества образования (PISA и TIMSS), r = 0.9 с учетом коррекции на ненадежность измерений (Lynn, 2008).

С другой стороны, в проведенном Э. Хантом и В. Виттманом иерархическом регрессионном анализе показатели по PISA оказываются наиболее мощным предиктором ВВП, по отношению к которому интеллект не добавляет значимо объясняемой дисперсии (Hunt, Wittman, 2008).

Таким образом, правдоподобно заключить, что компетентности действительно выступают опосредующим звеном между интеллектом и экономическими показателями. К этому, однако, нужно добавить, что формальные показатели системы образования, такие как средняя продолжительность обучения, охват населения различными уровнями образования и т. д., не являются сами по себе хорошими показателями приобретенных компетентностей.

Еще один вопрос, который заслуживает здесь рассмотрения, заключается в том, связаны ли экономические показатели со средним уровнем интеллекта населения или же с особенностями его распределения, например, размером интеллектуальной элиты или, напротив, уменьшением числа людей с чрезмерно низкими когнитивными способностями, не позволяющими заниматься сколько-нибудь квалифицированной работой. В рамках развиваемой модели это означает относительную важность для экономики решения задач разного уровня сложности. Конечно, средний интеллект населения и размер интеллектуальной элиты – связанные показатели, однако их корреляция не достигает единицы. Такие страны, как США или ЮАР, имеют больший разброс интеллектуальных показателей, чем, например, западноевропейские государства, следовательно, при одинаковых средних значениях интеллекта там окажется больше лиц, как входящих в интеллектуальную элиту, так и не способных к ведению квалифицированной работы.

В недавнем исследовании было показано, что национальная продуктивность, оцениваемая по числу патентов, в большей степени связана с численностью интеллектуальной элиты, чем со средним интеллектом населения (Gelade, 2008). Необходимо добавить, что число патентов – это показатель не столько работы всех индивидов в целом, сколько наиболее дееспособных и активных из них, поэтому сильная связь с размером интеллектуальной элиты не может вызвать большого удивления. В терминах предложенной модели можно выразить сказанное следующим образом: структура сложности задач в изобретательской деятельности, отражаемой в количестве патентов, не типична для таковой в экономике в целом.

Наконец, следует отметить, что исследования Линна показали экономическое значение не просто интеллекта, но генерального фактора интеллекта, т. е. фактически одномерной когнитивной способности. Это позволяет существенно упростить модель, отказавшись от многомерного представления способностей. Конечно, сводя способности к одному измерению, мы теряем некоторый объем информации. Весьма вероятно, что существует экономическое значение креативности в ее психометрическом понимании. Порой обсуждается специальная роль вербального интеллекта (Storfer, 1990). Однако уже одни только данные по экономическому значению генерального фактора интеллекта настолько существенны, что составленная на их основе модель позволяет делать весомые выводы. Формирование некоторых компетентностей требует определенных специальных способностей, но на глобальном уровне, изучавшемся Линном, речь идет о результирующей, которая отражается в генеральном факторе интеллекта.

Построение формальной модели

Изложенные положения модели дают основания перейти к ее формализации[7]. Эта формализация имеет двоякое значение. Во-первых, в практическом плане она открывает путь к количественным оценкам и тем самым сообщает модели предсказательные возможности. В частности, она позволяет дать экономические оценки различным сценариям работы с одаренными детьми. Во-вторых, в исследовательском плане формализация ускоряет процесс совершенствования теории, поскольку позволяет формулировать точные предсказания, соотнесение которых с действительностью выявляет нестыковки в теории и заставляет вносить в последнюю изменения. В то же время любая формализация связана со схематизацией, отбрасыванием части «пышно зеленеющего древа жизни» в пользу сухой теории. В особой степени это касается ее начальных этапов, когда закладываются принципы схематизации для той или иной области. Поэтому представляется, что оптимальным путем сегодня является сочетание двух подходов – номотетического, стремящегося к созданию абстрактных моделей, и идеографического, сохраняющего богатство живого представления о человеческой личности.

Вначале необходимо ввести функции, отображающие способности на компетентности и компетентности – на экономические достижения. Первая описывает, каким образом у групп людей, включенных в экономический процесс, на основе способностей формируются компетентности, и фактически является показателем работы образовательной системы страны. Функция, отображающая компетентности на экономические достижения, характеризует экономическую систему государства, а именно востребованность в ней высококомпетентных специалистов.

Для наших целей удобно сразу использовать одну функцию, являющуюся композицией двух перечисленных, поскольку при этом можно воспользоваться данными Р. Линна, которые приводят в соответствие способности и экономические достижения.

Для удобства последующих расчетов преобразуем оси интеллекта I и экономических показателей D таким образом, чтобы все данные Линна уместились в отрезках [0, 1]. Это достигается за счет следующего преобразования:

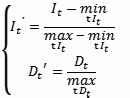
где индекс t обозначает соответствующую страну в данных Линна. Далее будем работать в новых осях, поэтому штрихи учитывать для удобства не будем.

Рассмотрим два варианта аппроксимации: при помощи степенной функции и при помощи показательной функции, которую предлагает Дикерсон (Dickerson, 2006). Мы пойдем по двум путям отдельно, а потом сравним полученные результаты.

Все степенные и показательные функции представим в виде трехпараметрического семейства:

F1(I; k, m, a) = m(I – a)k,

F2(I; k, m, a) = m × k(I – a).

Будем искать соответствующие функции f1(I) и f2(I) методом наименьших квадратов:

Следует отметить, что данные Линна имеют различную надежность для разных стран. Для большей части стран они основываются на эмпирических исследованиях, охвативших выборки большего или меньшего размера. Однако Линн расширяет свой список путем добавления стран, для которых интеллект оценен косвенно, в частности, путем сопоставления с интеллектом в соседних странах. Таким образом, мы располагаем менее обширным списком стран, для которых оценки интеллекта более надежны, и расширенным списком, для которого, однако, оценки интеллекта менее надежны. Расчеты были проведены отдельно по полному списку и – по сокращенному. В последний были включены страны, где данные по интеллекту были получены на выборке не менее 400 человек.

Линн сопоставляет свои данные по интеллекту с показателями ВВП за 2002 г. Более на дежно, однако, брать данные по ВВП не за один год, а за несколько, поскольку этим снижается влияние краткосрочных экономических факторов. Соответственно мы осуществили расчеты как на основании приводимых Линном данных за 2002 г., так и на основании усредненных показателей за 2002, 2006 и 2007 гг. Данные за 2006 г. были взяты с сайта Международной организации здравоохранения (World Health Organization), а за 2007 г. – с сайта Всемирного банка (World Bank). Данные за 2006 и 2007 гг. удалось получить не по всем странам, представленным в списках Линна, поэтому краткий список сократился на 6 стран, а расширенный – на 10. Из всех выборок исключены Китай и Экваториальная Гвинея.

Результат решения задачи для разных вариантов данных суммирует таблица 1.4.

На основании данных, представленных в таблице, можно заключить, что наиболее точно связь национального интеллекта и доходов на душу населения аппроксимирует степенная функция с показателями, варьируемыми от 2,08 до 2,6 для разных вариантов данных. Однако если взять показатель степени, равный 2, то полученная квадратичная функция, как видно из таблицы 1.4, аппроксимирует данные лишь чуть хуже, чем степенная с оптимально определенным показателем степени, и примерно так же (а для данных с достоверными коэффициентами интеллекта даже лучше), как это делает показательная функция. Стоит отметить, что точность аппроксимации в случае усредненных доходов на душу населения по трем годам оказывается выше, чем для одного года.

Далее мы проведем расчеты на основании двух моделей – квадратичной и степенной, а затем сравним сходство вытекающих из них оценок. Эти модели являются наиболее контрастными, поскольку степенная предполагает наиболее быстрый рост функции при возрастании аргумента, а квадратичная – наиболее медленный. Следовательно, степенная модель будет давать наиболее высокие оценки экономическому вкладу одаренной части населения, а квадратичная – самые низкие. В связи с этим, если оценки, полученные на основании двух моделей, окажутся достаточно близкими, это станет свидетельством высокой стабильности результатов, получаемых на основании предложенного подхода.

Таблица 1.4. Аппроксимация связи национального интеллекта и доходов на душу населения

Примечание: N – количество стран, k – полученный в результате решения задачи коэффициент степенной функции. В остальных трех столбцах отображены полученные нормы соответственно для степенной модели, для степенной модели с заданной степенью равной 2 и для показательной модели.

Вклад групп населения с различным интеллектом в экономику страны

Приведенные выше закономерности являются стохастическими, и возникает вопрос о причинах отклонений отдельных стран от аппроксимирующей зависимости. В контексте понимания экономики как решения задач ответ на этот вопрос включает несколько пунктов. Во-первых, для реализации интеллектуального потенциала людей необходимо, чтобы экономика в достаточном количестве предоставляла такие рабочие места, где необходим высокий уровень интеллектуальных компетентностей или же повышение их уровня приводит к повышению результата. Если в экономике минимальна потребность в квалифицированном труде, то и высокий интеллект граждан ничего не даст. Во-вторых, необходимо, чтобы существующие в стране рабочие места, связанные с решением наиболее сложных задач, приносили экономическую отдачу. Это условие также не всегда выполняется. В стране могут существовать рабочие места, например, в науке, которые требуют очень высокого интеллекта и компетентностей, однако наука не имеет в этой стране такого внедрения в экономику, которое позволило бы существенно увеличить национальный доход. Наконец, еще одним необходимым условием является наличие такой системы образования в широком смысле слова, которое позволяет формировать достойные компетентности на базе высоких способностей.

Страны, в которых высокий интеллект дополняется тремя перечисленными условиями, имеют высокие экономические достижения, но недостаточность хотя бы в одном звене из трех существенно снижает возможности реализации интеллектуального потенциала населения.

Проведенный анализ важен для перехода от интернационального уровня к национальному. Может ли быть перенесена полученная на наднациональном уровне зависимость интеллекта и ВВП на уровень внутри страны? Если вклад групп с различным уровнем интеллекта остается пропорциональным во всех странах, тогда закономерность допускает перенос. Если же снижение степени реализации интеллекта связано с понижением вклада наиболее интеллектуальных групп, то закономерности будут различными для стран, лежащих выше и ниже аппроксимирующей кривой.

Приняв допущение о пропорциональности вкладов, легко оценить, как вклады различных групп, так и отдачу, которую можно получить от работы с наиболее одаренными представителями населения. Однако при этом необходимо помнить, что условием этих подсчетов является указанное допущение. Если это допущение неверно, то для стран с высоким уровнем реализации интеллектуального потенциала оценки вклада наиболее интеллектуальных групп окажутся заниженными, а для стран с низким уровнем – завышенными. Это допущение в дальнейшем может быть проверено эмпирически на основе экономических данных по разным странам.

На основе принятой предпосылки оценим теперь вклад в экономические результаты страны групп населения с различным уровнем способностей. На первый взгляд может показаться, что функция, связывающая интеллект гомогенных в интеллектуальном отношении групп с их продуктивностью, и функция, связывающая средний интеллект страны с ее экономическими результатами, совпадают. В действительности, однако, это не так, причем одна функция может быть выведена из другой. Различим частный интеллект i, под которым подразумевается интеллект групп людей внутри страны, и интеллект I страны в целом. Под i может пониматься в том числе интеллект отдельного человека – гражданина той или иной страны. Мы будем полагать, что распределение интеллекта i подчинено нормальному закону с одинаковой дисперсией для всех стран.

Рассмотрим вначале квадратичную модель. Отметим, что нулем интеллекта имеет смысл считать значение, равное 60. В этом случае убирается коэффициент сдвига в степенной функции, и, кроме того, такое значение говорит о том, что для интеллекта ниже 60 отсутствуют производимые продукты, влияющие на экономические показатели. Это предположение с психологической точки зрения правдоподобно, поскольку значения коэффициента интеллекта, меньшие 60 баллов, соответствуют достаточно глубокой олигофрении.