Теория расчета оболочек нефтяных аппаратов

Константин Ефанов

Теория расчета оболочек нефтяных аппаратов

Посвящение

Монография посвящается Автору бионического дизайна, самого совершенного способа конструирования -

БОГУ ТВОРЦУ ТРОИЦЕ

Благодарность

Моей маме Татьяне Викторовне,

работавшей инженером в нефтяном машиностроении

Введение

Материал изложен относительно вопросов прочности при конструировании сосудов и аппаратов (нефтяных).

В первой части монографии рассмотрены некоторые аспекты теории тонких оболочек, теории толстых оболочек на основании решения задачи Ламе.

Подробно рассмотрена расчетная модель задачи Ламе и приведен ее критический анализ.

Универсальная теория оболочек приводится в форме логического следствия рассмотрения теории тонких оболочек и задачи Ламе.

Отдельно рассмотрены некоторые аспекты прочностного расчета элементов корпусов сосудов.

Рассмотрено применение элементов бионического дизайна.

1. Теоретическое основание норм расчета сосудов и аппаратов

Сосуды и аппараты стальные сварные в настоящее время нормами подразделяются на: сосуды до 21МПа и сосуды до 130МПа (сосуды высокого давления).

Сосуды этих двух групп имеют отличающееся конструктивное оформление. В качестве примера это могут быть форма днищ, узлов врезок штуцеров, рулонированное исполнение оболочки сосуда высокого давления.

По сложности нефтяные сосуды до 21МПа и высокого давления приблизительно одинаковые. Конечно, «не думающему» конструктору, специализирующегося на расчете и проектировании сосудов до 21МПа, сосуды высокого давления представляются повышенной сложности.

В соответствии с делением сосудов на 2 группы, для каждой группы применяются своя нормативная методика расчета на прочность.

В теоретическом основании методики расчета оболочек корпусов сосудов до 21МПа находится безмоментная теория тонких оболочек. Методика расчета сосудов высокого давления основана на теории толстых оболочек, построенной на решении задачи Ламе.

Сосуды (и оболочки в теории оболочек) делятся на тонкие и толстые по условному отношению толщины стенки к внутреннему диаметра (или радиусу). Отношение 0,1 означает погрешность расчета 10%. Для расчета в некоторых случаях можно допустить и большую погрешность расчета. В этом случае можно выполнять расчет сосудов высокого давления.

Сосуды до 21МПа относятся к тонкостенным сосудам, сосуды высокого давления относятся к толстостенным. Расчет толщины, соответствующей границе перехода по формулам из теории тонких оболочек и теории толстых оболочек может не совпадать.

Расчет корпуса сосуда высокого давления по теории тонких оболочек возможен до тех пор, пока толщина стенки удовлетворяет погрешности применения этой теории.

Погрешностью теории тонких оболочек является отношение толщины стенки к внутреннему диаметру (или радиусу) и назначается в долях или процентах.

Существуют сосуды со сравнительно толстой стенкой, но по критерию h/r относящиеся к тонкостенным сосудам, а по давлению к сосудам до 21МПа. Например, это может быть аппарат колонного типа для таких процессов, как гидрокрекинг. Такие оболочки возможно стоит проверять расчетом по уточненным методикам, например, по технической теории толстых оболочек не на основе задачи Ламе.

2. Варианты теорий оболочек

Теории оболочек, как написано выше, условно делят на теорию тонких оболочек и теорию толстых оболочек. Для каждого из типов теорий существует несколько способов построения в зависимости от гипотез. Теория тонких оболочек делится на техническую теорию с введенными гипотезами для решения определенных задач и математическую теорию, занимающуюся обоснованием теории.

Теория толстых оболочек на основе задачи Ламе подробно приведена в работах академиков Ильюшина А.А. [7], Работнова Ю.Н. [9]. В работе член-корреспондента А.И. Лурье [13] приведено решение задачи Ламе на основе пространсвенной теории упругости. В работе Ильюшина [8] приведена пластическая деформация толстой оболочки.

Теория толстых оболочек (т.е. на основе задачи Ламе) не имеет моментного решения и применяется решение из теории тонких оболочек. Расчетный аппарат теории толстых оболочек, построенной по задаче Ламе, но основании его возможностей не является лучшим средством для расчета сосудов высокого давления.

Следует в перспективе перейти на расчет сосудов по технической теории толстых оболочек, имеющей общий подход с теорией тонких оболочек. Техническую теорию толстых оболочек как более точную по сравнению с теорией тонких оболочек, можно распространить к применению на расчет тонкостенных сосудов. То есть выполнить переход на использование одной теории для расчета всех типов сосудов, что упростит работу расчетчиков и проектировщиков.

Теория тонких оболочек существует как техническая теория, направленная на расчеты конструкций, и как математическая теория, занимающаяся теоретически обоснованием.

Из технических теорий можно отметить теорию академика Власова В.З. [1], наиболее маститого российского (советского) специалиста по расчету оболочек. Ему также принадлежит вариант теории ребристых оболочек, под которую можно отнести по конфигурации обечайку с укрепляющими кольцами.

По математической теории тонких оболочек из российских (советских) специалистов можно отметить работы академика Новожилова В.В. [3, 4]. В работе [3] Новожилов писал, что теорию тонких оболочек необходимо рассматривать без отрыва от теории упругости. Из работ иностранных специалистов можно отметить книги иностранного члена академии наук Тимошенко [15] и Лява А. [18].

3. Построения расчётного аппарата вариантов теорий

В теории тонких оболочек из стенки оболочки выделяется кольцевой сегмент. В теории толстых оболочек на основе задачи Ламе, также в начале построения теории из стенки выделяется кольцевой сегмент. Затем построения теории идут по полностью отличающимся путям.

Сегмент выделяется секущими плоскостями, проходящими через ось оболочки. На примере цилиндрической обечайки:

Сегмент в плане представляет собой геометрическую фигуру трапеции с криволинейными основаниями (но не кубический или прямоугольный элемент):

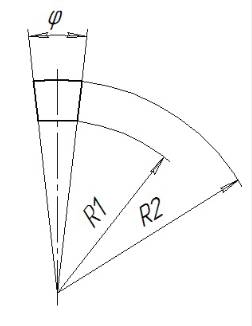
Рис. – Кольцевой сегмент является твердого тела (элементом твердого тела).

__

В теории тонких оболочек кольцевой сегмент заменяется плоским элементом его срединной поверхности. Напряжения по граням кольцевого сегмента рассматриваются как напряжения на элементарных площадках, расположенных на площади грани. Аналогично теории балок, напряжения по площади суммируются по интегралу, для которого пределами являются половина толщины стенки от срединной поверхности. В итоге вместо напряжения на гранях трехмерного твердого тела кольцевого сегмента заменяются усилиями и моментами на сторонах плоского элемента срединной поверхности.

Здесь важным является отметить, что на плоской элемент действуют и усилия и моменты. И в результате расчетный аппарат теории тонких оболочек позволяет рассчитывать и усилия и моменты, то есть имеет моментную теорию.

В теории толстых оболочек по задаче Ламе твердое тело кольцевого сегмента сразу заменяется твердым телом кубического элемента, который рассматривается в теории упругости в разделе о главных напряжениях. Тензор напряжений, конечно, является математическим термином. Здесь имеется в виду кубический элемент сплошной среды, по граням которого действуют главные напряжения.

Обращаю внимание, в связи с последующим изложением, для кубического элемента имеется направление расположения, при котором по его граням будут действовать только главные напряжения. Направление главных напряжений и ориентация этого кубического элемента как правило отличается от направления напряжений от нагрузки и соответствующего им кубического элемента.

Как уже отмечалось выше, теория толстых оболочек не имеет моментного решения. Объяснить это можно отсутствием моментов в расчетной модели.

__

Сравнительная таблица построения теорий тонких и толстых оболочек:

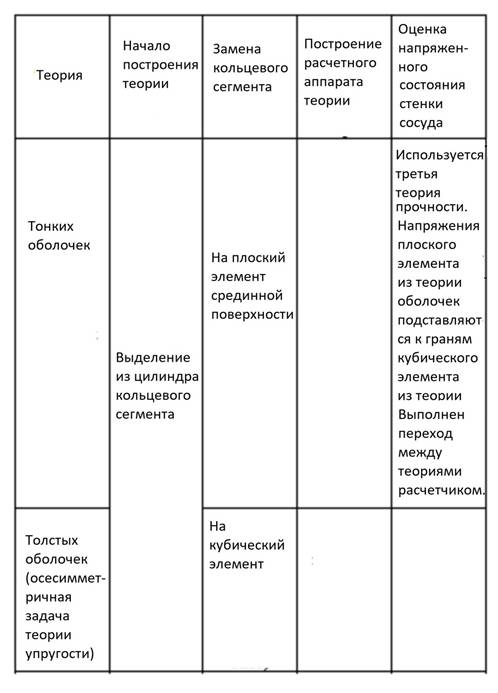
4. Теория тонких оболочек

Напряжения на сторонах выделенного сегмента раскладываются на составляющие:

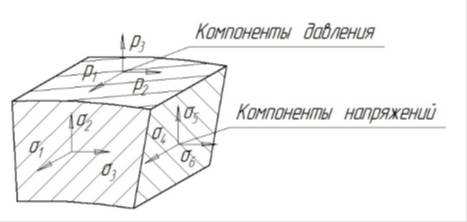
Затем вместо кольцевого сегмента вводится расчетная модель плоского элемента сегмента срединной поверхности:

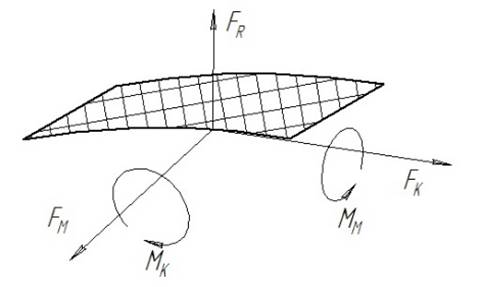
На ребра плоского сегмента действуют 3 усилия и 2 момента: FM, FK, FR – усилия меридиональное, кольцевое, радиальное; MM, MK – меридиональный и кольцевой моменты.

В некоторых книгах по расчету нефтяных и химических аппаратов указывается, что касательные напряжения присутствуют по кольцевым сечениям, но отсутствуют по меридиональным сечениям так как по условиям деформации их быть не может. Это ошибка. В этих работах выделяют кольцевой сегмент и к четырем его сторонам прикладывают 3 усилия и 2 момента.

В теории тонких оболочек, 5 нагрузок действуют не на весь сегмент (не на 4 стороны), а только на одну его сторону (на контур) [3].

По трем уравнениям безмоментной теории можно найти все напряжения в оболочке. Но в литературе по расчету аппаратов указывают о выводе расчетных формул только на основании уравнения Лапласа – одного из трех уравнений безмоментной теории. Система уравнений безмоментной теории статически определима и позволяет путем подстановки геометрии получить все выражения. А уравнение Лапласа содержит 2 неизвестных и не решаемо. Для решения подставляют геометрию с целью исключить одну из неизвестных и получить одно уравнение с одной неизвестной. Такой подход в сравнению с решением системы из всех трех уравнений выглядит менее обоснованно.

5. Осесимметричная задача теории упругости

В задаче Ламе из стенки толстого цилиндра выделяется кольцевой сегмент, к сторонам которого прикладываются напряжения:

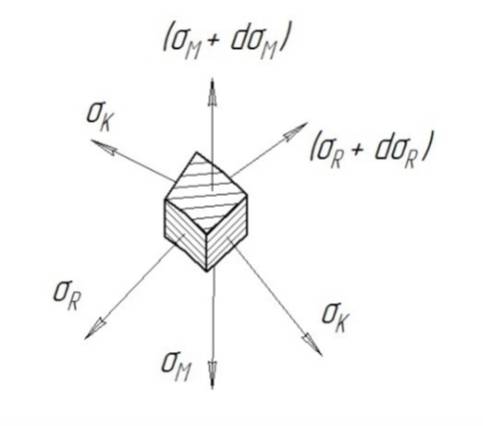
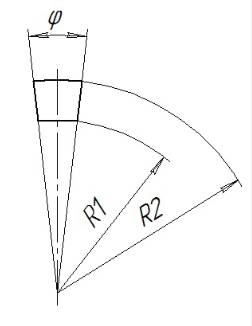
Геометрия сегмента в плане (трапеция с криволинейными основаниями):

Затем по факту происходит замена модели сегмента стенки на кубический элемент.

__

Цитата из работы известных авторов Даркова и Шапиро [11.с.596]: «…в связи с полярной симметрией цилиндра и нагрузки, нормальные напряжения являются главными напряжениями…». И дальше, что по площадкам главных напряжений отсутствуют касательные напряжения.

Задача Ламе приведена Г.Ламе во второй части его монографии по теории упругости в качестве примера применения выведенных им уравнений. Обоснованность полученных результатов решения применения формул Г.Ламе к расчету цилиндра определяется фактом отсутствия моментов в расчетной модели и в части замены кольцевого сегмента на кубический элемент. На основании рассмотрения расчетной модели можно сделать вывод о том, что расчетная модель в виде исходных данных к математическим выкладкам является неполной и, следовательно, результат решения задачи Ламе не является вполне корректным. Необходимо использовать подход с расчетной моделью, аналогичные используемым в теории тонких оболочек.

Теория толстых оболочек на основании решений задачи Ламе подробно изложена в работах академика Ильюшина А.А. [7,с.176].

Построение теории толстых оболочек производится для цилиндрической обечайки под действием одновременно внутреннего и внешнего давлений. Из стенки выделяется сегмент:

Почему-то принята расчетная модель сегмента с отсутствием касательных напряжений по боковым граням.

Разделяем понятия твердого тела и математического понятия тензора, которое используют в теории упругости для описания напряжения в точке.

Для осесимметричной оболочки в сферических координатах принято, что тензор напряжений выглядит в виде трапеции с криволинейными основаниями.

Отсутствие касательных напряжений по боковым граням объясняют симметрией такого тензора. Такое обоснование не справедливо, так как эти напряжения удерживают сегмент от вырова из параллельного круга. А на перпендикулярных гранях учитываемые касательные напряжения удерживают параллельные круги от взаимного смещения.

При переходе от прямоугольной системы координат к сферической системе координат меняется математическое описание тензора, но число сил и напряжений остается тем же в количестве 12 векторов.

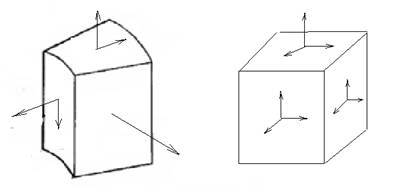
Как видно, в тензоре в сферических координатах не учитывают касательные напряжения по боковым граням. Кроме того, для сравнения укажем, что эти напряжения присутствуют в расчетной модели теории тонких оболочек.

За счет этого расчетная модель, на которой строится осесимметричная задача теории упругости, являющаяся теорией толстых оболочек является некорректной.

Для плоской задачи теории упругости происходит такое же некорректное отбрасывание касательных напряжений за счет симметрии, как указано в работе Безухова [19,с.138]: «Если распределение напряжений симметрично относительно оси… Из условий симметрии вытекает, что касательное напряжение τr

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.