Мир множества миров. Физики в поисках иных вселенных

Рис. 2.2. Уравнения Эйнштейна.

Тяготение пустого пространства

Когда общая теория гравитации была готова, Эйнштейн немедля применил ее ко всей Вселенной. Его не интересовали тривиальные подробности вроде положения конкретных звезд или планет. Вместо этого он стремился найти решение своих уравнений, которое в общих чертах описало бы строение всей Вселенной как единого целого.

В то время о распределении вещества во Вселенной мало что было известно, поэтому Эйнштейну пришлось делать определенные допущения. Он выдвинул простейшее предположение о том, что материя распределена в космосе в среднем однородно. При этом, конечно, существуют локальные отклонения от однородности, где концентрация звезд немного выше или ниже средней. Но в достаточно больших масштабах, согласно предположению Эйнштейна, Вселенная с хорошей точностью может считаться совершенно однородной. Это подразумевает, что наше положение в космосе ни в малейшей степени не является выделенным: все места во Вселенной более или менее одинаковы. Эйнштейн также предположил, что Вселенная в среднем изотропна, то есть из любой точки она выглядит примерно одинаково во всех направлениях.

И наконец, Эйнштейн предположил, что в среднем свойства Вселенной не меняются во времени. Иными словами, Вселенная статична. Хотя у Эйнштейна было мало наблюдательных подтверждений этому тезису, картина вечной неизменной Вселенной выглядела очень привлекательно.

Охарактеризовав искомую модель Вселенной, Эйнштейн мог теперь попытаться найти решение своих уравнений, которое описывало бы мир с желаемыми характеристиками. Однако ему не потребовалось много времени для того, чтобы выяснить: теория не допускает подобных решений. Причина была очень проста: массы, распределенные по Вселенной, отказывались оставаться в покое, а вместо этого “хотели” упасть одна на другую под действием своего гравитационного притяжения.

Это обстоятельство сильно озадачивало и сбивало с толку Эйнштейна. После года упорной работы он решил, что уравнения общей теории относительности следует модифицировать так, чтобы они допускали существование статического мира.

Эйнштейн знал, что, не нарушая физических принципов теории, в его уравнения можно включить дополнительный член. Эффект этого нового члена состоит в наделении пустого пространства, то есть вакуума, ненулевой энергией и натяжением. Каждый кубический сантиметр пустого пространства получает фиксированное количество энергии (а значит, и массу). Эйнштейн назвал эту постоянную плотность энергии вакуума космологической постоянной.[5]

Математическая структура уравнений Эйнштейна диктует, что натяжение вакуума в точности равно его плотности энергии и потому определяется той же постоянной. Натяжение вакуума аналогично натяжению резиновой ленты, которая сжимается, если ее отпустить. Натяжение противоположно давлению, которое заставляет предметы расширяться, подобно тому как шарик раздувается под давлением сжатого воздуха. То есть натяжение действует как отрицательное давление.

Если вакуум обладает энергией и натяжением, то как получается, что они не оказывают никакого влияния на нас? Почему мы не видим, что пустое пространство сжимается из-за собственного натяжения? Все дело в том, что не так-то просто заметить постоянную энергию или натяжение. Если увеличить давление в воздушном шарике, он раздуется. Но если на такую же величину увеличить давление воздуха вокруг него, то никакого эффекта не будет. Энергия вакуума неуловима, поскольку ее невозможно извлечь. Нельзя сжечь вакуум, нельзя использовать его для работы автомобиля или фена: его энергия задана космологической постоянной и не может уменьшаться. Выходит, что энергия и натяжение вакуума необнаружимы – за исключением их гравитационного воздействия.

Как оказалось, гравитация вакуума скрывала большой сюрприз. Согласно общей теории относительности давление и натяжение дают вклад в силу тяготения массивных тел. Если вы сжимаете предмет, его тяготение усиливается, если растягиваете – ослабевает. Обычно этот эффект очень мал, но если удастся растягивать предмет, не разрушая его, то в принципе можно ослабить его тяготение вплоть до полной нейтрализации или даже отталкивания. Именно это имеет место в случае вакуума. Отталкивающая гравитация натяжения вакуума значительно превосходит гравитационное притяжение его же массы, что приводит к отталкиванию.

Это в точности то самое, что требовалось Эйнштейну для разрешения его проблемы. Он мог подобрать значение космологической постоянной так, чтобы притягивающая гравитация материи находилась в равновесии с отталкивающей гравитацией вакуума, давая в итоге статическую вселенную. Из своих уравнений он вывел, что баланс достигается, когда космологическая постоянная равна половине плотности энергии вещества.

Поразительным следствием модифицированных уравнений было то, что пространство статической вселенной должно быть искривленным и замыкаться само на себя подобно поверхности сферы. Космический корабль, движущийся прямо вперед в такой замкнутой вселенной, в конце концов вернулся бы в исходную точку. Это замкнутое пространство называется трехмерной сферой. Ее объем конечен, хотя у нее нет границы.

Эйнштейн описал свою замкнутую модель вселенной в статье, опубликованной в 1917 году. Он признавал, что у него нет наблюдательных подтверждений ненулевого значения космологической постоянной. Единственной целью ее введения было спасение статической картины мира. Более десяти лет спустя, когда расширение Вселенной было уже открыто, Эйнштейн сожалел, что вообще выдвинул эту идею, и называл ее величайшей ошибкой в своей жизни.[6] После этого неудачного дебюта отталкивающая гравитация почти на полвека исчезает из мейнстрима физических исследований, но лишь для того, чтобы позднее вернуться с новыми силами.

Глава 3

Творение и его недостатки

Как ученый я просто не верю, что Вселенная началась со взрыва.

Сэр Артур Эддингтон

Вселенные Фридмана

В начале 1920-х годов вряд ли кто-то мог предположить, что замерзающий и голодный Петроград станет одним из тех мест, где случится очередной прорыв в космологии. Занятия в Петроградском университете едва возобновились после шестилетнего перерыва, вызванного войной и революцией. В холодной аудитории молодой профессор в очках читал лекции группе студентов, закутанных в шинели и меховые шапки. Профессора звали Александр Фридман. Лекции его были подготовлены тщательнейшим образом и подчеркнуто строги в математическом плане. В своем курсе Фридман затрагивал широкий круг тем: от математики и метеорологии – основных областей его специализации – до последнего увлечения молодого ученого – общей теории относительности.

Он восхищался теорией Эйнштейна и погрузился в ее изучение со свойственным ему энтузиазмом. “Я неуч, – часто говорил он. – Я ничего не знаю. Я буду еще меньше спать и не позволю себе никаких отвлечений, поскольку вся эта так называемая жизнь – лишь бесполезная растрата времени”.[7] Он словно бы знал, что у него в запасе всего несколько лет, а сделать предстоит еще много.

В совершенстве освоив математику общей теории относительности, Фридман сконцентрировался на проблеме, которую считал центральной, – строении Вселенной в целом. Из статей Эйнштейна он знал, что без космологической постоянной теория не имеет статических решений, но хотел выяснить, какие варианты решений все же возможны. И тут был совершен радикальный шаг, обессмертивший его имя. Вслед за Эйнштейном Фридман предположил, что Вселенная однородна, изотропна и замкнута, то есть имеет геометрию трехмерной сферы. Но он отбросил статическую парадигму и позволил Вселенной двигаться. Радиус сферы и плотность вещества могли теперь изменяться во времени. Отказавшись от требования статичности, Фридман обнаружил, что уравнения Эйнштейна имеют решение. Они описывают сферическую вселенную, которая начинается с точки, расширяется до некоторого максимального размера, а потом вновь сжимается в точку. В начальный момент, который мы теперь называем Большим взрывом, все вещество Вселенной упаковано в единственную точку, в которой плотность вещества бесконечна. Она убывает, пока Вселенная расширяется, и растет, пока та сжимается обратно, чтобы опять стать бесконечной в момент “большого схлопывания”, когда Вселенная вновь становится точкой.

Большой взрыв и “большое схлопывание” отмечают начало и конец Вселенной. Из-за исчезающе малого размера и бесконечной плотности материи математические величины, фигурирующие в уравнениях Эйнштейна, становятся неопределенными, а пространство-время не может продолжаться за этими точками. Такие точки называют сингулярностями пространства-времени.

Двумерную сферическую вселенную можно представлять расширяющимся и сжимающимся воздушным шаром (рис. 3.1). Закорючки на его поверхности изображают галактики, и по мере расширения шара расстояния между ними будут расти. Таким образом, наблюдатель в любой галактике видит, что остальные галактики разбегаются. Расширение постепенно замедляется гравитацией и в конце концов останавливается, сменяясь сжатием. На фазе сжатия расстояния между галактиками будут убывать, и все наблюдатели увидят, что галактики приближаются к ним.

Не имеет большого смысла спрашивать, куда расширяется Вселенная. Мы изображаем вселенную воздушного шара расширяющейся в окружающее пространство, но это не имеет никакого значения для ее обитателей. Они привязаны к поверхности шара и не представляют себе третьего, радиального измерения. Подобным образом для наблюдателя в замкнутой вселенной трехмерное сферическое пространство – это все существующее пространство, и вне его ничего нет.

∞

Вскоре после публикации этих результатов Фридман открыл другой класс решений с иной геометрией. Вместо искривления “на себя” пространство в этих решениях в определенном смысле искривляется “от себя”, что приводит к бесконечным (открытым) вселенным. Двумерным аналогом этого типа пространства является поверхность седла (рис. 3.2).

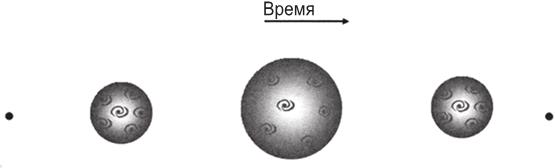
Рис. 3.1. Расширяющаяся и вновь сжимающаяся Вселенная.

И вновь Фридман обнаруживает, что расстояние, разделяющее любую пару галактик в открытой вселенной, растет, начиная с нулевого значения в сингулярности. Сначала расширение замедляется, но в данном случае гравитация недостаточно сильна, чтобы обратить его вспять, и со временем галактики приближаются к постоянной скорости удаления.

На границе между открытыми и закрытыми моделями находится вселенная с плоской, евклидовой геометрией.[8] Она хоть и расширяется без ограничений, но делает это как будто на пределе, так что скорость расширения становится со временем все меньше и меньше.

Замечательная особенность решений Фридмана состоит в том, что они устанавливают простую связь между геометрией Вселенной и ее конечной судьбой. Если Вселенная замкнутая, она должна вновь сколлапсировать, а если открытая или плоская, то будет расширяться вечно. В своих статьях Фридман не отдавал предпочтения ни одной из моделей.[9]

Рис. 3.2. Двумерный аналог открытой вселенной.

К сожалению, Фридман не увидел, как его работа стала основанием современной космологии. Он умер от брюшного тифа в 1925 году в возрасте 37 лет. И хотя его статьи были опубликованы в ведущем немецком физическом журнале, на них почти не обратили внимания.[10] Они были извлечены из небытия лишь в 1930-х годах, вслед за открытием Хабблом расширения Вселенной.[11]

Момент творения

Что бы ни говорили решения Фридмана о будущем Вселенной, самая неожиданная и интригующая их особенность – наличие начальной сингулярности, Большого взрыва, где перестает работать математика общей теории относительности. В сингулярности вещество сжимается до бесконечной плотности, и становится невозможно распространить решение на более ранние моменты времени. Таким образом, если воспринимать все буквально, Большой взрыв должен рассматриваться как начало Вселенной. Было ли это сотворением мира? Возможно ли, чтобы целая Вселенная началась с единственного события, случившегося конечное время назад?

Для большинства физиков это было чересчур. Такой одномоментный старт Вселенной выглядел как божественное вмешательство, которому, по их мнению, не должно быть места в физической теории. Но хотя для многих ученых “начало мира” было – и в большой мере остается – источником дискомфорта, оно дает и некоторые преимущества. Оно помогает избавиться от парадоксов, которыми полна картина статической, вечной и неизменной Вселенной.

Для начала, вечность Вселенной, по-видимому, противоречит одному из самых фундаментальных законов природы – второму началу термодинамики. Этот закон гласит, что физические системы эволюционируют от более упорядоченных состояний к менее упорядоченным. Если тщательно разложить бумаги по стопкам на столе и в окно неожиданно дунет порыв ветра, листы будут беспорядочно разбросаны по полу. Но вы никогда не увидите, чтобы ветер поднял бумаги с пола и сложил их аккуратными стопками на столе. Такое спонтанное уменьшение беспорядка не является принципиально невозможным, но оно настолько маловероятно, что увидеть подобное никогда не удается.

Математически степень беспорядка характеризуется величиной, называемой энтропией, а второе начало термодинамики говорит, что энтропия изолированной системы может только возрастать. Неуклонное возрастание беспорядка ведет в конце концов к состоянию максимально возможной энтропии, которое называется тепловым равновесием. В этом состоянии вся энергия упорядоченного движения превращается в тепло, и по всей системе устанавливается одинаковая температура.

На космические следствия второго начала термодинамики впервые указал немецкий физик Герман фон Гельмгольц в середине XIX века. Он отметил, что вся Вселенная может рассматриваться как изолированная система (поскольку по отношению к Вселенной не существует ничего внешнего). А раз так, то к Вселенной как к целому применимо второе начало термодинамики, и она должна неотвратимо приближаться к “тепловой смерти” – состоянию термодинамического равновесия. В этом состоянии звезды умрут и будут иметь одинаковую температуру с окружающей средой, а все движения, кроме беспорядочной тепловой толкотни молекул, остановятся.

Еще одно следствие второго начала термодинамики состоит в том, что если Вселенная вечна, то она должна была уже достичь термодинамического равновесия. И раз мы не находимся в состоянии максимальной энтропии, значит, Вселенная не могла существовать всегда.[12]

Гельмгольц не акцентировал этот второй вывод, а больше говорил о той части, которая касалась “смерти” (надо сказать, что такие настроения во многом поддерживались апокалиптической прозой конца XIX – начала XX века). Однако другие физики, в том числе такие титаны, как Людвиг Больцман, хорошо понимали эту проблему. Больцман видел выход в статистической природе второго начала. Даже если Вселенная действительно находится в состоянии максимального беспорядка, он может неожиданно чисто случайно уменьшиться. Такие события, называемые тепловыми флуктуациями, достаточно обычны в масштабе нескольких сотен молекул, но становятся все более невероятными по мере увеличения масштабов. Больцман предположил, что все наблюдаемое вокруг нас – это гигантская тепловая флуктуация в совершенно беспорядочной Вселенной. Вероятность возникновения такой флуктуации невыразимо мала. Однако даже невероятные вещи иногда случаются, если ждать достаточно долго, и они обязательно произойдут, если у вас в распоряжении бесконечное количество времени. Жизнь и наблюдатели могут существовать только в упорядоченных частях Вселенной, и это объясняет, почему нам повезло наблюдать столь неправдоподобно редкое событие[13].[14]

Трудность больцмановского решения состоит в том, что упорядоченная часть Вселенной выглядит чрезмерно большой. Для существования наблюдателя хватило бы превращения хаоса в порядок на масштабах, близких к размерам Солнечной системы. Это было бы намного более вероятно, чем флуктуация размером в миллиарды световых лет, необходимая для существования наблюдаемой нами Вселенной.

Другая проблема, имеющая более длинную предысторию, возникает, если предположить, что Вселенная бесконечна, а звезды более или менее однородно распределены по всему ее пространству. В этом случае, в каком бы направлении мы ни взглянули на небо, луч зрения в конце концов неизбежно должен упираться в звезду. А значит, все небо должно постоянно и ослепительно светиться. Встает простой вопрос: почему ночью темно? Иоганн Кеплер в 1610 году первым обратил внимание на эту проблему и пришел к заключению, что Вселенная не может быть бесконечной.

Как проблема энтропии, так и парадокс ночного неба естественным образом разрешаются, если возраст Вселенной конечен. Если она возникла лишь определенное время назад и изначально пребывала в высокоупорядоченном состоянии (с низкой энтропией), тогда сегодня мы наблюдаем деградацию от этого состояния к хаосу и не должны удивляться, что состояние максимальной энтропии еще не достигнуто. Парадокс ночного неба разрешается, поскольку во Вселенной конечного возраста свету очень далеких звезд еще не хватило времени, чтобы дойти до нас. Мы можем наблюдать лишь звезды, находящиеся в пределах радиуса горизонта, равного расстоянию, пройденному светом за время, равное возрасту Вселенной. Ясно, что число звезд в пределах этого радиуса конечно, даже если вся Вселенная бесконечна.

После таких аргументов как может хоть кто-то верить, что Вселенная существовала вечно? Но дело, конечно, в том, что идея возникновения космоса конечное время назад тоже порождает проблемы, способные поставить в тупик. Если Вселенная появилась в некоторый момент в прошлом, то чем определялись начальные условия Большого взрыва? Почему Вселенная началась с однородного и изотропного состояния? Ведь она могла возникнуть в любом другом. Должны ли мы приписать этот выбор Творцу? Неудивительно, что физики не торопились бросаться в объятия космологии Большого взрыва и предприняли множество попыток увильнуть от разрешения “проблемы начала”.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Примечания

1

А. Х. Гут, Инфляционная Вселенная, Addison-Wesley, Reading, 1997, p. 2. Глава 2. Взлет и падение отталкивающей гравитации

2

К примеру, время можно измерять в годах, а расстояние – в световых годах. (Световой год – это расстояние, проходимое светом за год.) Тогда скорость света c = 1.

3

Письмо Эйнштейна Эренфесту. Цит. по: A. Pais. Subtle is the Lord (Oxford University Press, Oxford, 1982).

4

Письмо Эйнштейна Зоммерфельду, 8 февраля 1916 г.

5

Фактически Эйнштейн не дал никакого физического объяснения новому члену. Его современная интерпретация как энергии вакуума и давления была предложена позднее бельгийским физиком Жоржем Леметром.

6

Позднее стало понятно, что эйнштейновская статическая космологическая модель неприемлема даже чисто теоретически, поскольку равновесие притягивающей и отталкивающей гравитации в этой модели является неустойчивым. Если по какой-то причине размеры вселенной Эйнштейна немного увеличатся, плотность вещества уменьшится (поскольку вырастут расстояния между галактиками), тогда как плотность энергии вакуума останется неизменной, будучи зафиксированной космологической постоянной. Следовательно, отталкивающая гравитация вакуума станет теперь сильнее притягивающей гравитации вещества и заставит вселенную расширяться. Это приведет к дальнейшему увеличению объема и еще большей разбалансировке притягивающих и отталкивающих сил. Вселенная, таким образом, войдет в режим ускоряющегося расширения. Аналогично, если размеры статической вселенной немного уменьшатся, притягивающая гравитация вещества победит отталкивание вакуума, и вселенная сколлапсирует в точку. Согласно квантовой теории, небольшие флуктуации размеров вселенной неизбежны, и поэтому вселенная Эйнштейна не может оставаться в равновесии бесконечно долго.

7

Цит. по: Э. А. Тропп, В. Я. Френкель, А. Д. Чернин. Александр Александрович Фридман. М.: “Наука”. – 1988. – с. 133.

8

Фридман не рассматривал случай плоской вселенной. Он был изучен Эйнштейном и де Ситтером в 1932 году.

9

Простая связь между геометрией и судьбой Вселенной сохраняется, только если считать нулевой плотность энергии вакуума (космологическую постоянную). Подробнее об этом в главе 18.

10

Достойным внимания исключением была реакция Эйнштейна на работу Фридмана. Сначала Эйнштейн думал, что Фридман ошибся, и написал короткую заметку в журнал о том, что он считал ошибкой. Однако менее чем через год, после беседы с другом Фридмана Юрием Крутковым, он отказался от своих возражений. Крутков сообщил домой, что он победил в споре с Эйнштейном и что “честь Петрограда спасена!”. Но хотя Эйнштейн и согласился с математическими выкладками Фридмана, он по-прежнему верил, что Вселенная статична, а работа Фридмана представляет лишь чисто формальный интерес. В своей второй заметке в журнале он писал, что “убедился в том, что результаты г-на Фридмана корректны и ясны”. В первоначальном черновике он добавил, что эти результаты вряд ли могут иметь какое-то значение для физики, но потом зачеркнул данную фразу, видимо, поняв, что она основана в большей мере на его философских предубеждениях, чем на каких-то известных фактах.

11

Модель расширяющейся Вселенной была переоткрыта в 1927 году Жоржем Леметром. Как и работа Фридмана, статья Леметра оставалась совершенно неизвестной вплоть до открытия Хаббла.

12

Источник энергии звезд не был известен во времена Гельмгольца, но теперь мы знаем, что они сжигают ядерное топливо, превращая водород в гелий, а затем и в более тяжелые ядра. Это необратимый процесс, сопровождаемый повышением энтропии, и в конце концов звезды исчерпывают свое ядерное топливо. Некоторые звезды выключают свои ядерные двигатели без большой помпы и потом постепенно остывают, другие взрываются, распыляя газ по межзвездному пространству и оставляя после себя компактный остаток (нейтронную звезду или черную дыру). Выброшенный газ может повторно послужить для формирования нового поколения звезд, но раньше или позже поступления газа иссякнут, поскольку все большая его часть будет заканчивать свой путь в компактных звездных остатках. Спустя триллион лет галактики, вероятно, значительно потускнеют. Процесс постепенного угасания огней может порядком затянуться, но одно ясно: Вселенная, какой мы ее знаем, не может существовать вечно.

13

Больцман установил связь между энтропией и беспорядком, прояснив тем самым смысл второго начала термодинамики.

14

Идея Больцмана о флуктуациях – это, возможно, первый пример того, что позже стали называть антропной аргументацией (см. главу 13).