Гравитация и эфир

эВ.

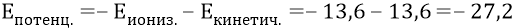
Ранее мы уже приводили подобную энергетическую диаграмму (рис. 21.4 и 21.7), подтверждающую эти последние цифры.

По определению, разность потенциалов (напряжение) между двумя «точками» поля (ядра) равна отношению работы поля при перемещении положительного заряда из начальной точки в конечную к величине этого заряда:

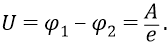
Но работа А (по определению) равна изменению потенциальной энергии, взятому с обратным знаком:

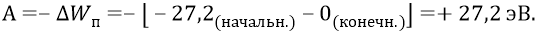
В результате величина

– отрицательный потенциал.

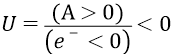
Действительно, «отрицательная обкладка конденсатора» (орбита) заряжена (электроном на ней) отрицательно. Таким образом, начальным потенциалом

(орбита) является величина:

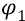
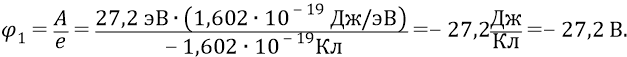
Конечный потенциал

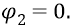
Поэтому первая атомная орбита находится под отрицательным напряжением величиной:

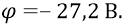
Другая «обкладка» атомного конденсатора (протон) заряжена положительным напряжением

по отношению к первой орбите с отрицательным на ней электроном.

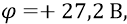
Поскольку под зарядом любого конденсатора понимается модуль заряда одной из его обкладок, а мы в атомных переходах оперируем лишь с переходами отрицательного электрона, то всегда будем считать, что наш конденсатор заряжен отрицательным зарядом (электрона) до отрицательного потенциала атомной орбиты.

По мере возбуждения атома, когда электрон будет переходить на всё более высокие (всё более удалённые от протона) орбиты, «атомный конденсатор», хотя и не будет разряжаться (на «верхней» обкладке будет кружить всё тот же электрон), но напряжённость поля между обкладками (а следовательно, на орбите) будет уменьшаться, поскольку будет возрастать ёмкость конденсатора из-за увеличения размеров его «электронной» обкладки:

и тогда напряжённость

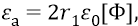
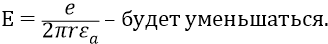
Вычислим теперь величину напряжённости того поля (протона), которая действует на электрон на уровне его первой орбиты:

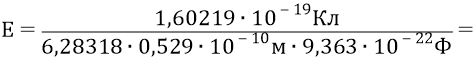
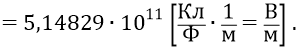
Сейчас мы слегка отвлечёмся от темы в сторону электротехники. Обратим внимание школьника на то, что величина такой напряжённости – абсолютно гигантская для нашего макро-мира привычных нам предметов:

То есть эта напряжённость поля в миллион раз больше, чем та напряжённость, которая наблюдается между проводами и землёй в знаменитых высоковольтных линиях передач, протянувшихся через всю нашу страну под названием ЛЭП-500. В этих линиях провода находятся под напряжением 500 кВ (пятьсот киловольт или пятьсот тысяч вольт). Такую линию, содержащую 3 мощных провода (трёх-фазное напряжение), держат металлические опоры высотой 30 метров. Сечение каждого провода – 400

(2х2 см). По каждому проводу протекает ток порядка 600 А (1,5 А на каждый 1

). Провода изолируют от металлических опор стеклянными гирляндами длиной до 5-ти метров – каждая. Расстояния между каждым из 3-х проводов – более метра. Но и при таком расстоянии слышен характерный «треск», особенно усиливающийся во влажную погоду. Это «трещат» микро-воздушные разряды тока между проводами и влажным воздухом. Если бы расстояния между проводами были единицами сантиметров, то разряды были бы постоянными и высоко токовыми. То есть воздух уже не выдерживал бы напряжения между проводами порядка 500 киловольт.

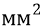
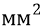
Но внутри атома напряжение между электроном первой орбиты и протоном ядра (разнесёнными на расстояние

) в миллион раз выше, чем напряжение в ЛЭП-500 между проводами, разнесёнными на метр (на самом деле мгновенные напряжения между фазными проводами чуть меньше номинала 500 кВ, но не в разы меньше, но лишь на проценты величины номинала). Почему же в атоме нет никаких пробоев, при столь малых расстояниях между зарядами, между которыми на этих малых расстояниях действуют гигантские напряжённости поля? Потому что в атоме между зарядами нет никакого «воздуха», состоящего из самих атомов, но есть лишь вакуум-эфир, а сами заряды не падают друг на друга (то есть не превращаются в «токи», выражаясь макро-языком электротехники) не потому, что они не подчинены законам электростатики, но потому, что одновременно подчинены законам механики, которые совместно с квантовой физикой (как «родителем» электростатики) являют нам резонансную систему, работающую по законам классической физики.

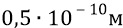
Оценим теперь порядок внутриатомных напряжённостей другим способом. Ещё раз вспомним, что потенциалом точки электростатического поля называется отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду:

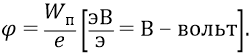
Значения потенциальных энергий для первой и второй орбит (в абсолютных величинах): 27,2 эВ и 16,34 эВ. Потенциалы же этих орбит: 27,2 В и 16,34 В. Разность потенциалов между орбитами:

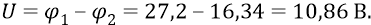
Напряжённость поля между 1-ой и 2-ой орбитами:

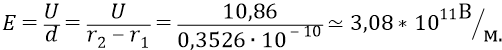
Мы получили среднее значение напряжённости между 1-ой и 2-ой орбитами

которое оказалось, естественно, меньшим напряжённости уровня первой орбиты, расположенной ближе к источнику поля – протону:

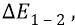
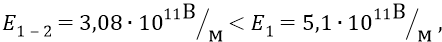
что соответствует физике поля ядра атома.

Однако вернёмся к проблеме наших разногласий с физиками, по поводу действительного распределения поля в атоме по мере удаления электрона по возрастающим номерам орбит.

* * *

Сейчас перейдём к конкретным цифрам. Начнём с расчёта потенциалов и энергий первой боровской орбиты, но будем оперировать не теорией квантовой механики, но классикой физики. Сначала – предварительное замечание. Поскольку в теории квантовой механики физики отошли от внутриатомных полей и потенциалов, но ограничились лишь энергиями переходов между стационарными атомными орбитами, то в своей литературе (как и во всех учебниках физики) они используют обозначение энергии буквой «Е». Но в классике этой же буквой обозначают напряжённость электрического поля. Поэтому мы, в классической физике, оставим это обозначение для напряжённости поля. Энергию же (как кинетическую, так и потенциальную) будем обозначать (только в этом разделе наших исследований) буквами

,

, … (потенциальные энергии уровней орбит) и

,

, … (кинетические энергии электронов на соответствующих орбитах).

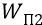
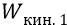
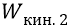
Итак, открывая любой учебник физики, с приведённой там диаграммой уровней энергии, например, атома водорода, мы обязательно найдём в качестве одной из энергий, выраженной в нанометрах наблюдаемой спектроскопистами линии, величину

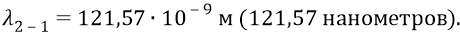
Это основная спектральная линия, излучаемая возбуждённым атомом при переходе его электрона со второй орбиты на первую. В теории Бора уровень первой орбиты –

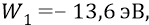
уровень второй орбиты –

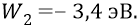
Поэтому разность этих уровней –

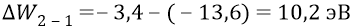
или

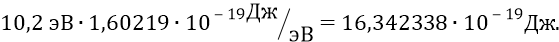
Далее по формуле Планка находим частоту, излучаемую атомом при переходе 2–1:

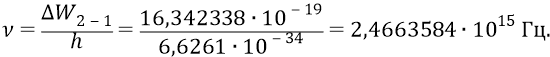
Длина волны излучаемого фотона:

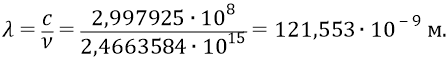
Так думают физики, вот уже 100 лет подряд уверенные в том, что такую длину волны излучает атом водорода при переходе в нём электрона с орбиты 2 на орбиту 1. Эта длина волны относится к серии Лаймана.

Однако мы утверждаем, что в конкретном единичном атоме не найдётся такой энергии (10,2 эВ), которой будет соответствовать длина волны излучённого фотона 121,553 нм, но найдётся только половинка энергии (5,1 эВ) – как вдвое меньшая планковская «порция энергии», которая, следовательно, могла бы дать вдвое меньшую частоту излучаемого фотона и вдвое большую длину его волны 243,106 нм. Однако спектроскописты не видят у атома водорода такой линии излучённого им спектра, но видят всё ту же линию 121,553 нм. Почему? Мы ответим сейчас на этот вопрос (по его физике), хотя этот ответ пока не будет для многих убедительным. Дело в том, что переход 2–1 с его энергией 5,1 эВ (а именно эта дельта энергии существует в реальном атоме, о чём мы утверждаем) происходит в «нижних» полях атомного ядра, ближних к ядру. В этих полях напряжённость поля значительно (в несколько раз) больше, чем те уровни напряжённости, которые были бы в атоме, если бы там существовал переход 2–1 с дельтой энергии 10,2 эВ. Большая часть такого последнего перехода происходила бы в более «верхних», более далёких от ядра полях, а следовательно, в более слабых.

И вот далее мы делаем фундаментальное утверждение для теории атома:

чем дальше от атомного ядра происходит переход электрона с орбиты на орбиту, тем медленнее, тем более плавно происходит этот переход. То есть тем медленнее успокаивается атом в его этом переходном процессе, выдавая для спектроскопистов большую длину волны фотона, излучаемого в этом переходе. Поэтому, возвращаясь к нашим цифрам, мы можем сказать, что переход с энергией 5,1 эВ, но происходящий в высоких полях напряжённости, ближних к ядру, может происходить так же быстро, как переход 10,2 эВ (если бы такой был в реальном атоме), но который происходит большую часть его времени в более слабых напряжённостях более дальних от ядра полей.

Однако сейчас мы прервёмся в подобных объяснениях для того, чтобы заполнить необходимую для дальнейших наших исследований таблицу соответствия номеров орбит атома, напряжённостей полей на уровнях этих орбит и полных энергий, соответствующих этим орбитам.

Дадим пример методики заполнения этой таблицы (таблица 21.1). Радиусы всех орбит находим по нашей формуле равномерного распределения орбит с шагом длины волны кванта эфира лёгкого слоя электромагнитного вакуума Метагалактики:

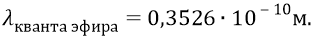
Формула для радиусов орбит:

Так, радиус первой орбиты:

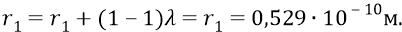
Радиус второй орбиты:

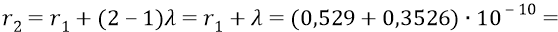
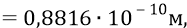
и так далее – для следующих орбит.

Затем вычисляем значения напряжённостей поля на уровнях орбит по нашей формуле (повторим её здесь для первой орбиты:

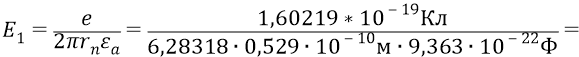
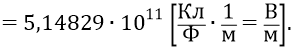
В следующем столбце таблицы вычислены потенциальные энергии атомной системы для уровней орбит по классической формуле:

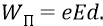
Здесь e – это заряд электрона, перемещаемый в поле протона (Е); вообще говоря – из бесконечности (как из точки нулевого потенциала поля протона) в точку нахождения электрона (на какую-то атомную орбиту). Но уточним – чем является здесь расстояние d для нашего случая «атомного конденсатора». Вспомним, что потенциальную энергию атомной системы в основном состоянии атома (для уровня первой электронной орбиты) мы уже находили, отталкиваясь от практического значения энергии ионизации 13,6 эВ. Для сдвинутой «вниз» энергетической шкалы с нулевым уровнем энергии, соответствующим удалению электрона на бесконечность, то есть уровню свободного от атома электрона, уровень потенциальной энергии атома оказывался вдвое меньшим полной энергии атома (–13,6 эВ) и составлял величину

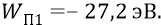
При этом тем потенциалом, под которым находился электрон первой орбиты, был потенциал (–27,2 В). Проверяем:

если потенциал поля первой орбиты равен (–27,2 В), то потенциальная энергия атомной системы с электроном в ней на первой орбите равна –

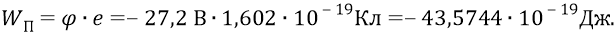
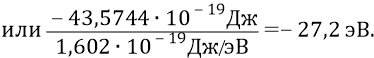
Но тогда то расстояние d, на которое был перемещён заряд электрона для того, чтобы поместить его в потенциал (–27,2 В), определится следующим образом:

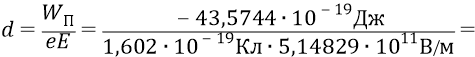
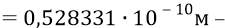
это радиус удаления первой орбиты от протона – как источника поля «атомного конденсатора». То есть если одна «обкладка конденсатора» у нас заряжена положительно (протон – источник поля), то вторая обкладка заряжается отрицательно (отрицательный электрон с зарядом

и уровнем напряжённости орбиты – E, отнесённой от источника поля на расстояние d).

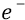
Однако далее мы вправе выбрать уровень напряжённости поля первой орбиты

за тот начальный, от которого затем, по мере удаления от ядра на уровни следующих орбит, напряжённость поля будет убывать в соответствии с множителем удаления –

(функция гиперболы).

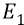
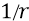
Здесь сделаем важное замечание. Классический пример конденсатора – это конденсатор с параллельными друг другу обкладками равной площади. Существенно то, что поле E внутри такого конденсатора – однородное. И поэтому в нём электрическое поле E при перемещении заряда (у нас – электрона) совершает работу:

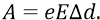
Причём эта работа электростатической силы в консервативной потенциальной системе, во-первых, не зависит от формы траектории перемещаемого заряда, во-вторых (по определению) равна изменению потенциальной энергии, взятому с противоположным знаком:

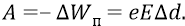
В нашем же «атомном конденсаторе» поле Е – неоднородно и изменяется по закону

Следовательно, выбирая за точку отсчёта поля его уровень на первой орбите

, мы можем записать:

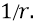
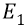
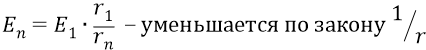
с ростом номера орбиты n.

Но потенциальная энергия системы

в поле источника изменяется в зависимости от

– как от расстояния точки нулевого потенциала (бесконечность) до точки «около источника поля», при том, что поле E в формуле для потенциальной энергии

однородно, то есть неизменно вдоль каждой силовой линии. То есть для того чтобы воспользоваться формулой, связывающей потенциальную энергию

, поле E и расстояние d, нам надо как бы выровнять наше неоднородное поле и сделать его как бы (по исходной формуле для потенциальной энергии плоского конденсатора) однородным, то есть таким, когда заряд, удаляясь от источника поля (от положительной обкладки конденсатора), двигался бы по одной и той же неизменной силовой линии поля, не убывающей по закону

, но остающейся неизменной по силе её воздействия на заряд (электрон).

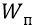
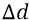
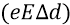
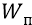
Но сейчас мы сделаем хитрый ход (по отношению к задаче получения требуемой формулы, согласующейся и с теорией о потенциальной энергии, и с реалиями изменения поля в «атомном конденсаторе». Мы перенесём закон

от изменения по нему напряжённости Е на изменение по нему перемещения заряда

в поле источника. При этом учтём тот факт, что в нашем «конденсаторе» перемещение заряда по удаляющимся орбитам происходит равномерными дискретами

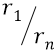
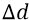
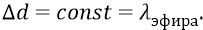
Запишем формулу:

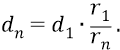
В ней закон изменения расстояния орбиты от её номера n – квадратичный и точно такой же

как закон изменения напряжённости

в зависимости от номера орбиты n. Так, при очень больших номерах n расстояние

стремится к нулю, то есть стремится к точке нулевого (самого «высокого» по номерам орбит) потенциала поля источника. По мере же уменьшения номера орбиты величина

растёт, достигая самого своего большого значения

в точке орбиты

. Поэтому, сравнивая формулы для

и

в зависимости от члена

(закон

), мы можем воспринимать закон изменения потенциальной энергии не в зависимости от изменения перемещения заряда в однородном поле, но в такой же зависимости изменения напряжённости поля (теперь – неоднородного) в равномерном «пересчёте» номеров орбит:

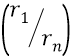
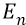
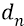
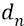
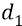
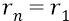
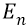
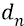
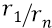
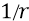
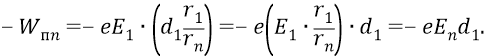
Напомним, что потенциальная энергия (

) отрицательна. Поэтому уменьшение напряжённости

с ростом номера n соответствует уменьшению отрицательной величины, то есть увеличению потенциальной энергии атомной системы.

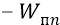
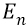
Найдём, например, значение потенциальной энергии для положения системы с электроном на второй орбите:

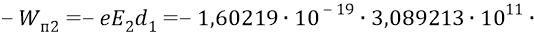
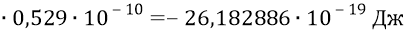
или

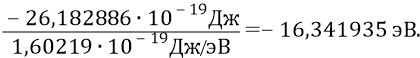
Теорема вириала говорит нам о том, что кинетическая энергия электрона второй орбиты должна быть вдвое меньше абсолютного значения потенциальной энергии системы:

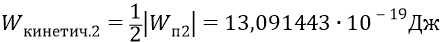
или 8,1709678 эВ.

По ходу дела, в отличие от физиков, в нашей квантовой физике мы можем найти величину линейной скорости электрона на второй атомной орбите (как и на всех других):

Полная энергия атомной системы для уровня второй орбиты электрона:

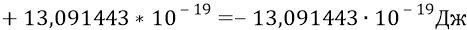
или –8,1709678 эВ.

Аналогичным образом мы вычисляем значения потенциальных энергий системы для всех других орбит и заносим их в таблицу 21.1.

Далее вычислим, например, длину волны фотона, излучаемого атомом в переходе 2–1.

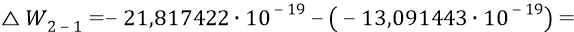
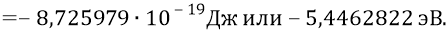
По формуле Планка частота соответствующего фотона должна была бы определиться следующим образом:

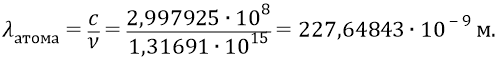
Однако, забегая вперёд, мы (здесь – пока без объяснений) скажем о том, что порция энергии

излучаемая в переходе, принадлежит на самом деле не полному фотону, видимому физиками, но лишь одной полуволне этого полного фотона. То есть тот фотон, который видят физики, соответствующий переходу 2–1, излучается сразу двумя разными атомами в одно и то же время. Поэтому действительной порцией энергии, соответствующей полному (двух полупериодному фотону), должна быть энергия вдвое большая найденной нами, то есть энергия: