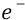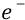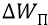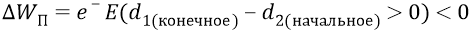полная версия
полная версияГравитация и эфир
Однако мы сильно отвлеклись от конкретики обсуждаемой темы атомных орбит. Но сначала – снова классика. Напомним школьнику, что такое потенциал и напряжённость поля. Квантовая физика сильна тем, что она может (наконец-то!) объяснить школьнику физический смысл тех макро-характеристик электростатики и электродинамики (типа «потенциала», «напряжения», «напряжённости»), о которых школьник уже слышал, но очень плохо их понимает (мы это утверждаем, то есть утверждаем то, что школьник плохо понимает все эти характеристики).
Итак, во-первых, затронем некоторые основы электростатики. Что такое «заряд» вообще и заряд электрона – в частности? Для электростатики «заряд» – это просто электрическое поле частицы – как поток квантов, «излучаемых», например, электроном («из электрона») во все от него стороны пространства. Электрон – это стандартная космическая частица, которая всегда пребывает в стандартном космическом эфире, имеющем стандартные космические характеристики (такие как плотность распределения квантов – частиц, скорость их движения, масса этих частиц, их конструкция и наконец – их «полярность» – как некоторое чисто конструктивное отличие друг от друга «положительных» квантов – частиц эфира от «отрицательных» частиц этого же эфира, о чём физики пока ещё абсолютно не знают). Кстати, физики не только не знают, что такое «электрический заряд», но они не знают, что такое электрон.
Во-вторых, сейчас (объясняя «заряд») мы находимся внутри атома, где действуют (взаимодействуют) два «заряда»: «заряд электрона» и «заряд протона». Заряд электрона, с точки зрения объяснения характеристик электростатики, мы жаргонно будем называть словом «электрон» и обозначать его символом «
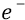
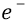
В-третьих, и заряд электрона (как поток – поле всегда излучаемых им частиц эфира), и заряд протона (как аналогичный поток излучаемых им частиц) в атоме (для простоты – одноэлектронном, то есть в атоме водорода), эти потоки – жёстко поляризованы, как и жёстко поляризованы сами частицы – электрон и протон. То есть вся картинка их взаимных полей лежит строго в одной и той же «тонкой-тонкой» плоскости, в пределе имеющей «толщину» размера частицы – электрона, совпадающую с «толщиной» частиц-кварков, из которых состоит протон, которые (эти там кварки) быстро вращаются внутри протона, являя нам некоторое «колёсико», излучающее из себя во все стороны этого «колёсика» суммарное поле протона (но излучающее строго – в плоскости этого колёсика), поле, состоящее, вообще говоря, из суммы полей кварков, но в результате равное по величине (по силе) точно такому же «заряду», который излучает электрон.
И теперь, словно бы «конструируя» атом, мы будем плавно вносить откуда-то очень издалека (в пределе – из бесконечности) отрицательный «электрический заряд» (частицу электрон вместе с его полем) в потенциальном поле положительного «электрического заряда» (протона-частицы, вместе с его полем). То есть мы будем совершать работу по перемещению единичного заряда (электрона) в потенциальном поле – из бесконечности в какую-то точку внутри атома, на уровень удаления какой-то орбиты от протона. Поскольку в данной главе мы занимаемся лишь некоторыми оценочными цифрами (точными займутся физики, если захотят, а не захотят – займутся школьники), то для простоты будем вносить электрон на уровень, допустим, n – ной орбиты атома. Почему именно n – ной? Если мы внесём электрон на уровень первой орбиты, то он окажется под потенциалом поля протона уровня десятка вольт, а если внесём его на уровень n – ной орбиты, то он окажется там под потенциалом поля протона величиной всего лишь, допустим, в десятые доли вольта (эти потенциалы вычисляются физиками в общем случае методами спектроскопии). То есть разность потенциалов поля протона в точках первой и n – ной орбит составит величину напряжения между этими точками:
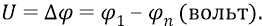
Самым важным результатом здесь будем считать тот, что разность потенциалов (напряжение) между точкой первой орбиты и точкой n – ной орбиты почти равна разности потенциалов (напряжению) между любой из точек первой орбиты и «бесконечностью».
Зачем нам понадобилось привязывать потенциалы к орбитам 1 и n? Это нужно только для того, чтобы задать точное расстояние между двумя фиксированными точками потенциального поля протона – ∆d. Потому что расстояние между любой точкой поля вблизи протона и далёкой бесконечностью (как истинное ∆d для истинного потенциала) измерять, мягко говоря, неудобно. Но это ∆d нам необходимо знать потому, что классика физики определяет через него напряжённость поля (поля протона, в данном случае):
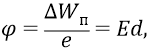
где
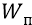
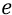
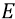
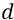
Начнём с закона, проверенного временем. Таким, главным в электростатике, является закон Кулона:
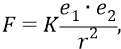
где заряды
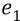
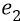
K – электростатическая постоянная, о которой мы будем ещё говорить ниже.
Если поле создаётся зарядом
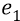
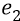
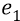
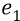
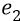
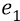
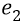
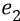
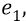
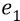
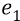
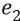
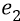
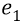
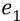
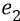
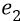
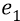
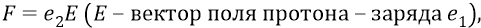
откуда напряжённость поля в данной точке равна отношению силы, с которой поле (заряда
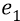
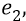
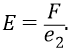
Фактически оба последних выражения – это определения в электростатике силы поля и напряжённости этого поля. Сразу же разберёмся с размерностями величин.
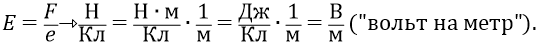
В вольтах измеряется разность потенциалов между двумя точками электрического поля. О ней мы ниже будем подробно говорить.
Если напряжённость поля E – это вектор и силовая характеристика поля, то потенциал φ – это скаляр и энергетическая характеристика поля.
Потенциалом точки электростатического поля называется отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду:
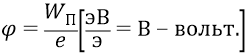
Фактически потенциал – это та же энергия, которую придали заряду, поместив его в данную точку поля:
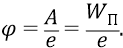
Здесь заряду
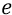
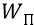
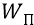
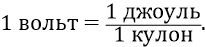
Но поскольку кулон для атомных процессов – это гигантская величина, то здесь работают с единицей заряда не «кулон», а «заряд электрона». Эта единица составляет очень малую часть от заряда – кулона:
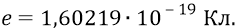
Поэтому для получения той же единицы потенциала – «вольта» энергию уменьшают в такое же число раз и получают новую единицу энергии – «электрон-вольт» (эВ):
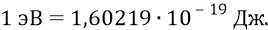
Тогда
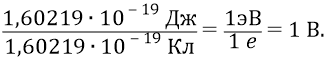
Здесь в энергию «электрон-вольт» включена единица заряда – «e» (заряд электрона). Поэтому для получения чистого потенциала «1 вольт» надо эту энергию нормировать к единичному заряду (разделить на величину единичного заряда).
Таким образом, один «электрон-вольт» – это та энергия, которую надо затратить для того, чтобы единичный заряд e переместить из бесконечности (точка нулевого потенциала поля) в ту точку внутри атома, потенциал которой будет отличаться от нулевого на один вольт. И тогда в этой точке энергия единичного заряда (электрона) будет равна величине – «электрон – вольт».
Теперь – о «разности потенциалов». Так же как для потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта этого потенциала, то есть зависит от выбора той точки поля, потенциал которой принимается нулевым. Но изменение потенциала не зависит от выбора нулевого уровня отсчёта потенциала.
И вот далее надо быть предельно внимательными. Повторим ещё раз с существенным уточнением. Электростатика называет потенциалом любой данной точки поля (поля протона – у нас) отношение работы силы поля по перемещению положительного заряда (именно положительного) из данной точки поля в бесконечность (на уровень истинного нулевого потенциала поля), к этому заряду:
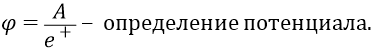
У нас, внутри атома, поле направлено от «положительного заряда» – протона во все стороны от него – в бесконечное от него удаление. В определении потенциала говорится о перемещении положительного заряда (в поле протона, хотя мы будем перемещать «отрицательный заряд» – электрон). Определения в электростатике возникли задолго до открытия структуры атома, с его электронами и протонами, и эти определения мы не можем изменять. Точно также как не можем изменять определение направления протекания тока в проводнике. Там, задолго до «электронов», было принято называть «током проводника» движение «положительных зарядов». Хотя потом выяснилось, что в проводнике на самом деле движутся «отрицательные заряды» (электроны), а «положительные заряды» (протоны атомов) благополучно стоят на месте в составе атомной решётки проводника. Но первичные определения в физике никто не меняет, во избежание неимоверной, в таком случае, путаницы.
Теперь выберем в поле протона две точки (рис. 21.3), находящиеся на одной «силовой линии» поля: «нижнюю» точку 1, более близкую к протону, и «верхнюю» точку 2 – дальнюю от него. Тогда электрическое поле протона Е совершит положительную работу А по перемещению положительного заряда из начальной точки 1 в конечную 2:
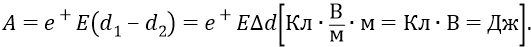
Эта работа не зависит от формы траектории, поскольку (вспоминаем) совершается консервативными силами (это те силы, которые, двигая тело в поле сил по замкнутой траектории, совершают в сумме нулевую работу). Эти «консервативные силы» нам, внутри атома, – как нельзя кстати. Потому что здесь не важно, говоря о потенциалах, на какую точку одной и той же орбиты мы переносим тело (электрон), но важно – на каком уровне потенциальной энергии находится эта орбита.
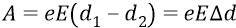

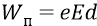
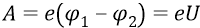
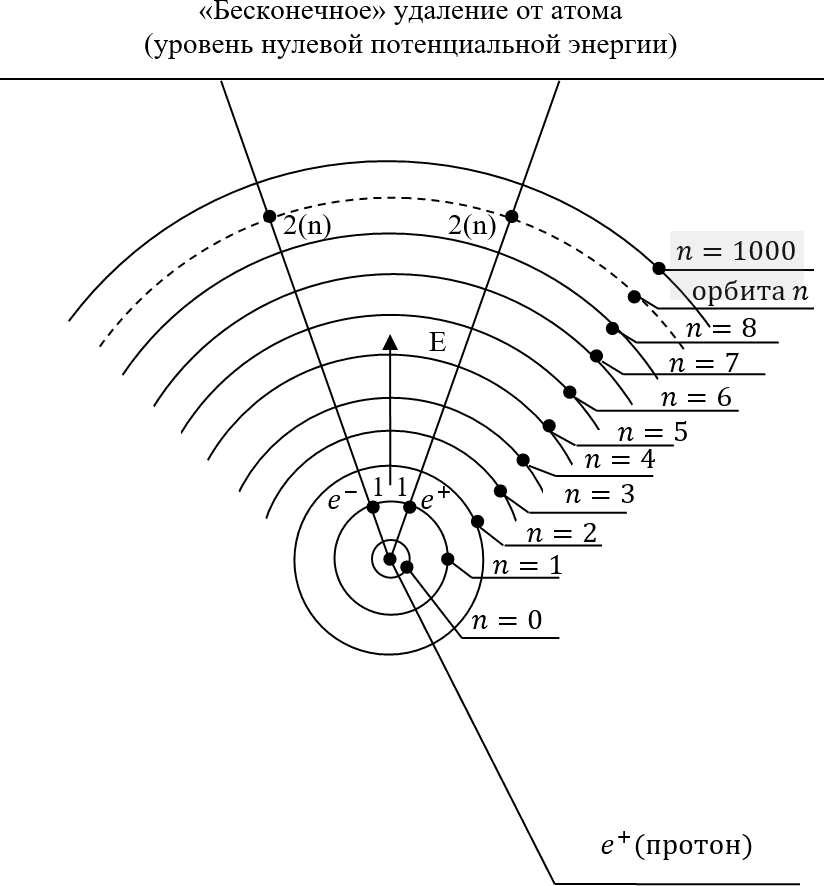
Рис. 21.3
Итак, поскольку работа электростатической силы является консервативной, то эта работа равна изменению потенциальной энергии, взятому с противоположным знаком:
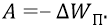
Проверим действенность классических определений в их применении к атомным процессам, происходящим при перемещении заряда внутри атома. Сначала будем перемещать положительный заряд
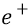
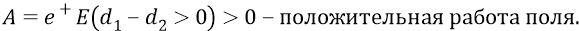
Здесь учитываем то обстоятельство, что расстояние внесения заряда из бесконечности в точку 1 больше расстояния внесения заряда из бесконечности в точку 2.
Но (по определению) изменение потенциальной энергии системы – это разность между её конечным и начальным значением:
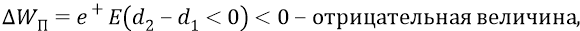
что совпадает с классическим определением – «изменение потенциальной энергии тела (у нас – заряда
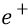
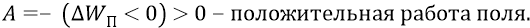
Ещё раз подчеркнём, что в этих формулах величина
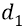
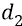
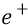
Ещё раз. Если «изменение потенциальной энергии» может иметь знак за счёт изменения положения точки поля (

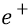
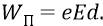
Здесь
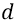
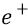
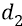
Теперь рассмотрим другой случай: перемещаем какими-то сторонними силами положительный заряд
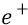
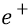
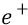


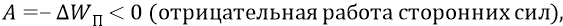
изменение потенциальной энергии
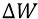
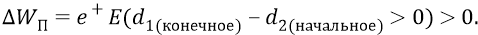
И наконец, мы переходим к реальной атомной системе с отрицательным зарядом
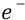
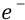
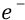
При падении электрона