Гравитация и эфир

Кроме того, эта «миговая» гравитация способна излучаться только нижними – левыми по рисунку частицами. Правые же частицы вообще не способны будут излучать в сторону электрона никакую гравитацию, поскольку всегда будут обращены в его сторону только рёбрами своих колец. Но «рёбрами» никакая частица не излучает.

Итак, горизонтальная поляризация электрона очень сильно защищает его от «нижнего» гигантского, но «вертикального» поля Земли. Единственным исключением здесь явится боковая – горизонтальная для электрона воздушная оболочка атмосферы Земли. Она будет оказывать на электрон полномасштабное сильное гравитационное излучение. Но если опыт проводится в ясную погоду, при отсутствии по горизонту облаков, то такое «горизонтальное» гравитационное излучение воздушной атмосферы должно быть сильно изотропным, то есть действующим на электрон в каждый миг его прямолинейного движения одинаково со всех сторон – направлений.

Рассмотрим теперь кинематику эксперимента. Если смотреть на установку со стороны Луны, то наш опыт будет точь-в-точь похож на школьную задачку о бросании камня вдоль горизонта и его падении на Землю в потенциальном гравитационном поле Земли. Только у нас вместо камня будет электрон, а бросать мы его будем в потенциальном гравитационном поле Луны. Сначала смотрим со стороны Луны в горизонтальную плоскость, которая касается поверхности Земли, а вернее – касается пика горки, где расположена наша установка. Источник электронов находится от нас (со стороны Луны) в левом торце цилиндра трубы, электрон летит слева-направо к электрону-анализатору. По ходу своего движения к экрану электрон будет отклоняться в нашу сторону (в сторону Луны). А теперь посмотрим на ту же картинку горизонтальной плоскости сверху. Луна окажется внизу картинки, а электрон летит слева-направо (рис. 20.11).

Запишем кинематическое уравнение движения материальной точки (электрона). В потенциальном поле это движение – равноускоренное:

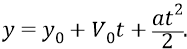
Но поскольку электрон у нас отклоняется в отрицательную сторону оси «y», то знак ускорения «

» будет отрицательным. Ось координат выбираем таким образом, чтобы начальное отклонение было нулевым.

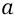
В этом кинематическом уравнении скорость

– это не скорость полёта электрона, но это начальная скорость «падения» электрона в потенциальном поле Луны. Эта скорость в этот начальный момент равна нулю, поскольку электрон, начиная своё движение направо, только начинает падать в поле Луны. Поэтому в данном случае уравнение приобретает окончательный вид:

Отклонение электрона в горизонтальной (по отношению к Земле) плоскости XOY

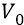
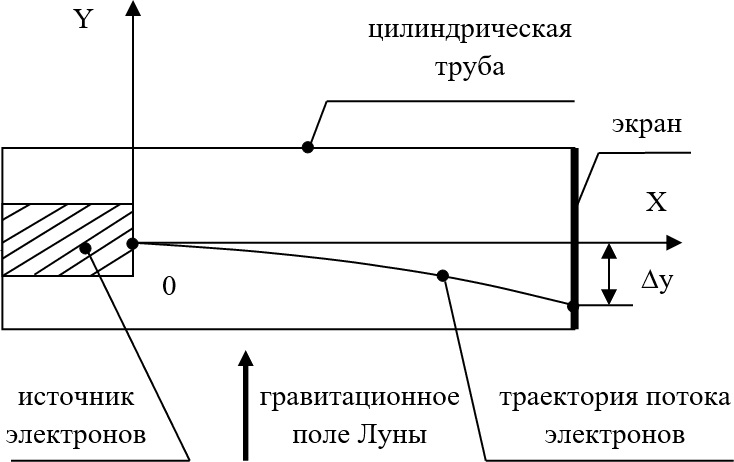
Рис. 20.11

Теперь нас будет интересовать ускорение свободного падения электрона, которое в этой формуле не зависит от начальной «боковой» скорости электрона. То есть электрон делает одновременно два независимых движения: 1). Он летит слева-направо с постоянной «боковой» скоростью; 2). Он свободно падает «вниз» с ускорением

в гравитационном поле Луны.

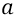
Для того чтобы найти «

» рассмотрим два фундаментальных уравнения Ньютона. Первое – это второй закон:

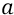
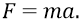
Второе – это закон всемирного тяготения:

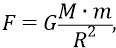
где M – масса Луны

, m – масса электрона, R – расстояние от Земли до Луны (384 000 км). Сравнивая эти два уравнения, замечаем, что второе уравнение можно записать как:

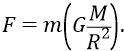
Здесь

– это всё та же масса электрона. Но второй сомножитель в последнем уравнении – это фактически ускорение свободного падения электрона в поле Луны:

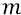
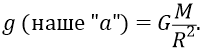
Вычислим его значение:

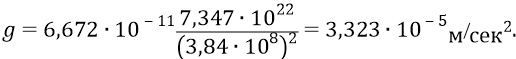
Проверим по этой же формуле значение ускорения свободного падения на поверхности Луны, при радиусе Луны 1737 км:

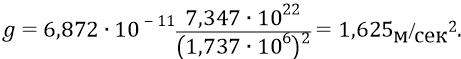
Это ускорение меньше, чем ускорение падения тел на поверхности Земли в

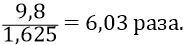
То есть все тела любой их массы весят на Луне в 6 раз меньше, чем на Земле. Известный факт.

Найденное же нами значение ускорения тел, находящихся на Земле, под действием гравитационного поля Луны, говорит о том, что любое земное тело притягивается Луной с ускорением

(33 микрона) в секунду за каждую последующую секунду.

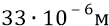
И поскольку время пролёта электрона в цилиндре установки составит (в первом приближении) величину (для активной дистанции электрона от источника до экрана 6 м,

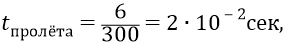
то за это время электрон на экране отклонится («упадёт» в поле Луны) на малое расстояние:

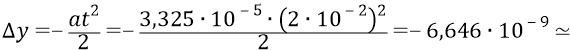
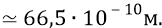
Это в 66 с половиной раз больше размера атома по его первой орбите. Такое отклонение физики обязаны обнаруживать с помощью специальной обработки электрического потенциала места падения электронов на экран. Можно тщательно продумать электронную схему анализатора. А если учесть тот факт, что при вращении трубы-цилиндра мы будем в любом случае иметь колебательный процесс отклонения трассы электронов в разные стороны, то на выходе электронного блока обработки анализатора должен получаться сигнал, в первом приближении похожий на некую синусоиду, колеблющуюся относительно центрального («нулевого») положения её амплитуды.

То есть если физики (или студенты университета) обнаружат в подобном опыте такую «синусоиду» на выходе анализатора отклонения потока электронов, то можно будет считать, что этот поток (ток) отклоняется никаким не электромагнетизмом, но, во-первых, только гравитацией, во-вторых, только полем массы «гигантской» Луны. Больше – нечем.

К великому сожалению, поле Луны для подобных экспериментов – строго монотонно. Но если бы оно было хотя бы в некоторой степени колебательным, то можно было бы думать об измерении скорости передачи гравитационного сигнала. И поэтому (то ли к сожалению, то ли к счастью) колебательные источники гравитации нам (нашим физикам) придётся придумывать самим. Нельзя бесконечно получать от Природы подарки: надо и самим начинать работать.

Завершим тему оценкой некоторых параметров установки. Для удешевления эксперимента не будем предъявлять высокие требования к скоростным и прочностным параметрам установки. Так, в простейшем случае трубу-цилиндр придётся вращать вручную. За время выгодного «горизонтального» положения на небе Луны, установку можно повернуть, допустим, до десятка и более раз, снимая показания аппаратуры и затем усредняя эти показания, что позволит минимизировать «механический дребезг» показаний от механических деформаций трубы. Поэтому, для минимизации подобных деформаций придётся использовать трубу-цилиндр с диаметром не менее 10-ти сантиметров и достаточно толстыми стеками (не менее 5 мм). Такую 6-ти метровую трубу (можно 3-х метровую, но для неё соответствующие характеристики придётся пересчитать) надо устанавливать на достаточно мощную станину (лист металла), приваренную к трубе. Станина-лист вращается на жёстко прикрепленном к ней ровно в центре трубы роликовом подшипнике скольжения большого диаметра. Подшипник же лежит на мощной станине, допустим, швеллера (15 см или шире), сваренного крестообразным способом. Идеальным здесь будет последующее бетонирование этого крестообразного швеллера в грунт.

Если же мы задумаем вращать эту установку двигателем, с частотой вращения, скажем, 10 оборотов в секунду, то все наши параметры (как «электронные», так и механические) «поплывут» в худшую сторону для электронных точностных характеристик, но в лучшую сторону для механических точностных. Сразу же скажем о том, что при частоте вращения установки 10 Гц трубу придётся «обкорнать» на порядок её длины – до 30-ти сантиметров активного участка «пушка-экран». Вся труба-цилиндр здесь будет иметь длину 0,5 м. Причём по 10 см с обоих концов займёт электронная аппаратура ускорителя и экрана (останется активная зона отклонения электронного луча – 30 см). Тогда, двигаясь со скоростью 300 м/сек, «измерительный» электрон преодолеет активный путь за время:

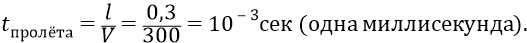
Найдём линейную скорость самой удалённой от центра вращения точки трубы-цилиндра, при угловой скорости вращения 10 оборотов в секунду

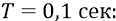
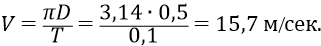
Потребуем, чтобы вес аппаратуры, размещаемой на концах цилиндра, не превышал одного килограмма (как аппаратуры источника, так и аппаратуры экрана). Тогда центробежная сила, действующая на аппаратуру и на трубу в целом, составит величину:

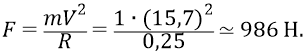
Если сравнивать эту силу с «весом» тел на поверхности Земли (они здесь подвергаются ускорению

), то сила «на разрыв» трубы-установки будет:

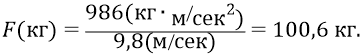
То есть аппаратура будет испытывать в этой «центрифуге» ускорение

Такое ускорение аппаратура обязана выдерживать. Но пересчитаем точностные «гравитационные» характеристики для данного случая:

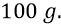
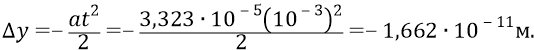
Это почти на порядок меньше размеров атома. Такое отклонение довольно трудно, но всё же можно обнаружить с помощью специальной электронной обработки. Но основной трудностью в таком последнем эксперименте (с частотой установки 10 оборотов в секунду) будет процесс разграничения полезного (гравитационного) отклонения электронного луча от его инерционного отклонения за счёт вращения установки. Правда, это инерционное отклонение при всегда постоянной скорости вращения будет тоже постоянным, а поэтому его, наверное, можно будет как-то учесть – скомпенсировать. Тем более что начальный опыт снятия показаний всегда будет производиться при покоящихся положениях измерительного цилиндра установки.

* * *

Таким образом, на последних страницах главы мы привели «целых» два метода измерения «гравитационного сигнала», хотя в качестве этого «сигнала» здесь выступило монотонно-постоянное гравитационное поле удалённого объекта (Луны). Но эти методы могут быть хотя бы каким-то, пусть самым начальным, но шагом вперёд в деле изучения явления гравитации. Но «колебание пространства» у физиков – это, безусловно, шаг назад в деле освоения гравитации.

Здесь мы практически ничего не успели сказать о построении гравитационных передатчиков. Поэтому изложим хотя бы какие-то мысли для их дальнейшего обсуждения. Вот здесь, для построения передатчиков, вполне могут использоваться, наряду с электронными лучами – потоками, лазерные лучи. При этом, как лазерные фотоны (направленные потоки квантов эфира), так и электроны «состоят» из конструкций одинаковых ньютоновых масс. Следовательно, будет выигрывать тот пучок-линейка частиц, который будет обладать максимальной концентрацией частиц в кубическом сантиметре луча. Здесь скажем о том, что если гравитационная передающая «антенна» будет состоять из потоков-струек электронов, то эти потоки жёстко поляризованных электронов можно будет посылать буквально «один за другим», где, скажем, горизонтально поляризованные электроны будут чуть ли не касаться друг друга и при этом «не видеть друг друга», то есть нисколько не отталкиваться друг от друга (по вертикальным столбикам) своими «электрическими зарядами», которые будут действовать только в горизонтальных плоскостях каждого потока, но никак не будут мешать друг другу (не отталкивать друг друга) «верхние» электроны от «нижних». Таким способом можно создавать целую «высокую стенку» из сплошных «горизонтальных» потоков электронов или пучков электронов. То есть фактически будет создан экран довольно приличных размеров (например, 10 метров в высоту и 100 метров в длину), в котором одномоментно будут двигаться миллиарды миллиардов электронов (этой «мгновенной» площади). Кроме того, этот экран-антенну легко можно сделать «параболическим». Для этого поляризация электронов, начиная с нижних потоков и до верхних, должна меняться с любым угловым шагом, скажем, на

или меньше. И тогда излучение всей этой «вертикальной параболы» можно будет направлять в «горизонтальную линию» (где можно располагать приёмник гравитационного излучения), которую (эту линию) можно двигать от излучающей параболы на разные расстояния, начиная буквально с одного метра (фокуса) от параболы и далее – до сотен, тысяч и миллионов километров, посылая туда, в эту «линию» концентрированный гравитационный сигнал.

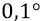
А если, к тому же, нам удастся через некоторые вертикальные промежутки (меридианы) установить поляризаторы (как поляризаторы лазерных лучей, так и поляризаторы пучков электронов), то мы сделаем, таким образом, и «горизонтальную параболу» потоков частиц. Тогда получим истинную «гравитационно-передающую тарелку», которая будет излучать наш гравитационный сигнал не «в линию», но уже «в точку», начиная от метра расстояния от антенны и заканчивая, пожалуй, миллиардами километров. Почему здесь можно говорить уже о миллиардах километров? Потому что мы будем посылать не «монотонную гравитацию», но гравитационный сигнал любой нашей модуляции. И поскольку будем его посылать электронным способом, то он будет следовать с высокой частотой повторения. А для такого сигнала, даже утопающего где-то вдали под толщей гравитационных шумов, «медленных» по отношению к нашему рукотворному, обязательно будет применена на «нашем» приёме – корреляционная обработка, которая позволит вытянуть наш полезный сигнал из-под этой толщи «хаотических-медленных» шумов, изначально превышающих наш сигнал на много-много порядков. Но такая обработка будет нужна, естественно, только в случае построения нашего же приёмо-передающего гравитационного канала.

Но в случае приёма дальней космической гравитации эта гравитация, естественно, не будет нужной нам прерывистой, да к тому же – заданно-прерывистой, то есть такой заданно-прерывистой, для которой мы могли бы применить заданную корреляционную обработку. Однако здесь само построение нами приёмной антенны по типу уже описанной параболической тарелки даст искомый результат. Причём «вертикальную параболу» (как горизонтальные пучки, распределённые по вертикали) мы никак не будем искажать электронно, что даст приём «чистой гравитации». Но вот вертикально установленные столбики поляризаторов, для параболического поворота горизонтальных потоков частиц, мы, безусловно, электронно искажаем, мешая, следовательно, приёму «чистой гравитации». Но, правда, мы её искажаем строго заданно. А поэтому эту строгую заданность нам непременно удастся учесть – скомпенсировать тогда, когда при приёме далёкого или близкого сигнала на неё наложится полезная нам «чистая гравитация».

Однако нельзя не сказать ещё об одном супер важном приёме обработки, который может позволить (уже при том, что антенна будет параболической) увеличить её коэффициент усиления ещё, пожалуй, в миллионы раз. Этот приём заключается в следующем.

Но сначала сделаем важное утверждение по самой физике излучения телами гравитационного поля в дальнюю или ближнюю зону от этих тел. Мы утверждаем, что эффективность гравитационного взаимодействия между макро-телами сильно уступает эффективности электромагнитного взаимодействия между ними не потому, что «маленькие» гравитационные кванты слабо «дёргают» гигантские по отношению к ним электромагнитные частицы, но потому, что они слишком редко дёргают их. В том смысле «редко», что гигантские потоки гравитационных квантов, излучаемые любым макро-телом, посылаются им в разные стороны от себя на много-много порядков большей интенсивности, чем посылаются точно на конкретную удалённую частицу, да ещё не просто «точно в её сторону» и даже не только «точно по площади её электромагнитного сечения», но точно по её малому-малому гравитационному ядру.

Ещё раз. Глядя, например, на рисунок 20.10, можно себе представить, что если, скажем, выделить на Луне огромный «кусок» её вещества, размером с кубический километр, то из миллиардов и миллиардов атомных частиц этого «кубика» будут точно «светить» на наше гравитационное ядро измерительного электрона только единицы частиц, поток гравитационных квантов от которых будет периодически «чиркать» по нашему ядру. Да и при этом, надо ещё попадать нужной поляризацией кванта по нужной поляризации ядра в микро-миг пересечения квантом поля Луны плоскости ядра электрона. То есть точное попадание квантом далёкого объекта по ядру удалённой от него частицы – это редчайшее квантовое событие. Но можно ли заданным способом повысить вероятность такого события? Для тех, кто будет строить приёмо-передающие гравитационные каналы, это делать не только будет «можно», но и «нужно». Иначе будешь всегда проигрывать «хаотической «паразитной» гравитации. И еще раз. Какой-нибудь лунный электрон, вращающийся по орбите какого-нибудь лунного атома, может посылать в сторону нашего электрона целые серии гравитационных квантов с любой сколь угодно великой частотой их повторения, но эти серии (даже тогда, когда их скользящий луч будет точно «чиркать» по ядру электрона) могут на какую-нибудь миллиардную долю угловой секунды пролетать мимо нашего ядра. И такая ситуация может длиться не только какие-нибудь секунды времени, но и часы или даже дни. Однако если мы заданно выделим каким-либо специальным способом какой-нибудь единичный электрон, кружащий на далёкой Луне вокруг ядра своего атома, и будем медленно-медленно поворачивать его орбиту таким образом, чтобы она точно своей плоскостью пересекала нашу земную трассу нашего измерительного электрона, да пересекала эту трассу много-много раз в секунду при заданном колебательном изменении плоскости орбиты лунного «излучающего» электрона, то эффективность гравитационного взаимодействия только двух названных удалённых электронов будет сравнима с эффективностью взаимодействия хаотического кубокилометра Луны и нашего электрона.

Поэтому, если в нашей параболической гравитационной тарелке передатчика мы заставим все потоки всех электронов или всех фотонов медленно вращать свою поляризацию мимо удалённой «точки», куда смотрит наша антенна, то «граммы» вещества наших заданно-направляемых нами потоков, по своей эффективности гравитационного взаимодействия с «точкой» превратятся в тысячи или миллионы тонн. Причём эти гигантские тонны будут мелькать относительно нашей удалённой точки-приёмника по принципу: в данную микросекунду эти тонны – «есть», а в следующую микросекунду – их «нет». И когда мы всё это «есть-нет» подвергнем в «точке» на приёме корреляционной обработке, то запросто вытянем наш заданный сигнал любой его модуляции из-под толщи гигантских гравитационных шумов.

Таким образом, беглый обзор темы гравитационного приёмника для приёма дальней гравитации говорит о том, что мы способны запросто, и уже «сегодня», поворачивая нашу приёмную гравитационную тарелку, настраивать её «в точку» на приём-просмотр не только всех наших планет Солнечной системы (запросто), но и на приём чуть ли не всех миллионов астероидов, которые в ней движутся самым разным образом. А также, учитывая то, что гравитационный направленный луч на много порядков по своей «пиковости-направленности» превышает любой электромагнитный луч, мы сможем, наконец, увидеть все планеты всех звёздных систем, отделяя эти планеты от их звёзд. Увидим мы, естественно, и все галактики Нашей Метагалактики. Но через некоторое время, развиваясь в данном направлении, мы увидим, наконец, соседнюю с нами другую Метагалактику. И это будет тем событием, которое скажет о том, что наша физика, наконец-то, достигла больших высот в своём развитии.

* * *

Какой главный вывод мы можем сделать по результатам данной главы? Он снова – не физический, но только философский. Главный вывод состоит в том, что поголовно все физики 20-го века отошли от Бога. Не тот человек Верит в Бога, кто говорит «я верю», но тот, кто делает (хоть и не все свои дела, по причине пока ещё слишком большой слабости людей, но хотя бы главные для человека дела), кто делает их в соответствии с Законами Бога. Главные дела для физиков – эффективно развивать физику-науку. Но физики 20-го века отошли от Законов Бога. Мы это здесь и сейчас утверждаем. И именно поэтому они получили тот глубочайший кризис, который виден теперь даже малому ребёнку.

Но может быть все земные люди всегда были слабыми, и просто поэтому они пока ещё продолжают оставаться таковыми? И тогда физики хотя бы в этом могут найти себе оправдание? Нет, не могут. Потому что задолго до нынешних физиков мы со школьниками уже наблюдали совсем других. Они – верили. И одним из них был Ньютон. Физики 20-го века обнаглели настолько, что они эту его Веру чуть ли не обсмеяли прилюдно. Упростили переводы его Законов. Превратили его Законы Природы (читай – Законы Бога) до каких-то безбожных чисто «физических». Мол: «Мы-то здесь занимаемся физикой; зачем здесь какой-то Бог? Божественным пусть занимаются теологи вместе со своей Церковью». Но Ньютон формулировал все свои законы – именно как Божественные Правила, обязательные для их следования людьми. Упростили. Обкорнали Ньютона. Докатились до философских безбожников типа Эйнштейна. Вот он как раз – именно говорил (не Верил, но говорил) то там, то тут что-то про Бога. И это «что-то» Власть подсовывала уже школьникам и студентам в качестве неких цитат: «Вот смотрите, и здесь он про Бога сказал, и здесь его упомянул». «Упомянул» – стыдно слушать таковую ересь.

Любой думающий человек, и не обязательно даже – физик, серьёзно знакомясь с устройством Вселенной (даже в том виде этого знакомства, который уже стал доступен учёным), может и должен поражаться той грандиозности и Красоте, с какими была построена Вселенная. Её конструкция, начальные условия и сама Жизнь так тщательно продуманы и заранее рассчитаны, что только Заведомый Разум мог это изначально предусмотреть. Думать, что всё это Великолепие получилось – возникло само по себе, без Разума – верх слабого легкомыслия.

Короче: хотите вы, физики, или не хотите, но придётся вам, всё же, вернуться в 21-ом веке ко всем четырём законам Ньютона – не как к законам «физическим», но как к Законам Божественным. Тогда и отпустит Он – Бог вас (может быть) из кризиса вашего позорного.