Седьмое доказательство

Скорость этого перехода тем больше, чем больше разница уровней (разность потенциалов). Очевидно, что поток воды Ниагарского водопада низвергается гораздо быстрее, чем, скажем, «течет река Волга – издалека долго».

Если в процессе энергообмена разность потенциалов выравнивается, скорость движения потока снижается до тех пор, пока оба уровня не уравновесятся. Тогда поток энергии прекратится, и система не сможет больше совершать работу.

Система в этом случае перейдет в равновесное состояние, характеризующееся нулевой энергией.

В нашем примере с чашкой чая это произойдет тогда, когда температура нагретой чашки сравняется с температурой остывшего чая (например, равновесие может быть достигнуто на уровне 500 С).

Обладает ли система, достигшая такого равновесия, какой-нибудь энергией?

Нет, не обладает. Потому что поток энергии прекратился, и никакая работа больше не совершается (в данном случае работа заключалась в нагреве чашки или в остывании чая).

Но ведь 50 градусов – это тоже энергия?

А это зависит от того, какую систему рассматривать.

Если в качестве изолированной системы рассматривать систему «чашка – чай», то для неё не имеет значения, какую температуру имеют оба компонента. Важно только то, что эта температура одинакова.

Если же включить в систему также и комнату, в которой находится чашка (предположим, что температура в комнате 200С), то в этой системе наша чашка с чаем, конечно, будет обладать энергией. До тех пор, пока не остынет до комнатной температуры. И тогда в системе «комната – чашка с чаем» тоже наступит равновесие, и энергия системы опять примет нулевое значение.

Продолжая расширять границы системы, мы придем к тому, что рано или поздно равновесие должно наступить в пределах всей Вселенной, и что её энергия станет равна нулю.

Таким образом, первое начало термодинамики утверждает, что любая совершаемая в изолированной системе работа (любое движение) ВСЕГДА ведет к уменьшению разности потенциалов, то есть к убыванию энергии системы, и НИКОГДА – к увеличению разности потенциалов.

Применительно к Вселенной это означает, что из нынешнего активного состояния Вселенная неизбежно движется в сторону потери энергии, и, рано или поздно, придет к состоянию с максимальной энтропией, к неактивному состоянию.

Давайте припомним вывод, сделанный нами в конце первой главы: Вселенная не вечна. Она движется навстречу неизбежному концу. Мы сделали этот вывод исходя из наблюдений за окружающим миром. Теперь мы видим, что он прямо вытекает из Первого закона термодинамики, который и объясняет склонность материи к разрушению. Материя ведет себя так не вследствие своего дурного характера, а подчиняясь фундаментальному закону Природы.

Согласно этому закону, материя не может бесконечно поддерживать свое существование.

Если бы это было возможно, был бы возможен и «вечный двигатель».

С 1775 года Парижская академия не принимает к рассмотрению проекты вечного двигателя ввиду очевидной невозможности его создания. Потому что «бессмертные», как именуют себя члены Парижской академии, в отличие от авторов проектов «вечных двигателей», знали Первый закон термодинамики.

Аристотель в XII книге «Метафизики» выделил две категории сущностей: одни – вечные, другие – преходящие. Вечные сущности не имеют ни начала, ни конца, они всегда существовали, и всегда будут существовать.

Преходящие сущности – это те, которые сотворены (возникли) и будут уничтожены (исчезнут). Преходящие сущности имеют начало и конец. К преходящим сущностям Аристотель относил, например, растения и животных. К преходящим сущностям относится и человек, поскольку он рождается и умирает.

Раз материальная Вселенная не вечна, она тоже относится к преходящим сущностям.

Материалисты, которые считают Материю всемогущей (в их системе мира Материя занимает место Бога), до недавнего времени наделяли ее чудесным свойством бессмертия и категорически отрицали факт ее сотворения (возникновения).

Однако такое представление находится в явном противоречии как с наблюдаемыми явлениями, так и с законами Природы. В том числе – с Первым законом термодинамики, согласно которому материальная Вселенная неизбежно движется навстречу своему концу.

Что имеет конец – то, конечно же, имело начало.

Не бывает конца без начала, как не бывает и начала без конца.

Впрочем, трудно убедить того, кто не хочет быть убежденным. Вера на то и вера, что ей не нужны доказательства. Материалистическая вера не исключение.

Первому закону термодинамики материалисты пытаются противопоставить Законы сохранения, полагая, что эти законы подтверждают их веру в вечную и несотворенную Материю.

Неужели один закон Природы может отменить другой?

Придется нам ненадолго отклониться от генеральной линии нашего повествования, чтобы развеять это заблуждение.

Глава 9. Законы сохранения

В 1668 году английский математик Джон Уоллис, исследуя поведение сталкивающихся тел, пришел к любопытному выводу. Он обнаружил, что в любой изолированной системе (такой, на которую не действуют никакие внешние силы) общее количество движения всех составляющих её тел всегда, при любых обстоятельствах, остается одинаковым.

Тела, составляющие систему, могут как угодно двигаться – с любой скоростью, в любых направлениях, соударяться, разбегаться, но сумма их движений всегда будет одной и той же, не увеличиваясь и не уменьшаясь.

Открытый Уоллисом закон получил название закона сохранения количества движения или закона сохранения момента.16

Если вспомнить, что единственная по-настоящему изолированная система – это Вселенная, наиболее общая формулировка закона сохранения количества движения может выглядеть так: «Сумма движений всех тел во Вселенной постоянна». Эта сумма никогда не меняется. Какие бы изменения ни происходили внутри системы, общий момент системы не меняется.

В 1748 году Михайло Ломоносов в письме к Леонарду Эйлеру высказал предположение о том, что не только общее количество движения в системе, но и общее количество вещества в ней (выражаемое массой) – величина постоянная. Тем самым был сформулирован закон сохранения вещества. А в 1774 году французский химик Антуан Лавуазье эмпирически подтвердил предположение Ломоносова, доказав, что в пределах изолированной системы некоторые тела могут терять массу, а другие наращивать, но общая масса системы остается постоянной.

С утверждением в науке понятия энергии различные явления, способные совершать работу (движение, тепло, свет, звук, электричество, магнетизм, химические изменения и т.д.) стали рассматриваться как разновидности энергии. Возникла мысль о том, что одна форма энергии может преобразовываться в другую, что некоторые тела могут терять энергию, а другие ее приобретать, но при этом в любой изолированной системе общее количество энергии постоянно. Первым высказал такую мысль немецкий физик Герман фон Гельмгольц, а в 1847 году ему удалось убедить в этом весь научный мир.

Альберт Эйнштейн

В 1905 году Альберт Эйнштейн вывел свою знаменитую формулу Е = mс2, связавшую энергию с массой. Закон сохранения массы утратил свое значение в качестве самостоятельного закона: стало очевидно, что он является частным случаем закона сохранения энергии.

Применительно к Вселенной (как изолированной системе) Закон сохранения энергии может быть сформулирован следующим образом: «Вселенная обладает некоторым количеством энергии, и это количество энергии всегда, при любых изменениях внутри Вселенной, остается неизменным, не прибавляется и не исчезает».

Когда был открыт закон сохранения энергии, сторонники материализма ликовали: они восприняли этот закон как главный аргумент в пользу вечности Вселенной, главное доказательство того, что материальная Вселенная никогда не возникала и никогда не уничтожится, что она всегда существовала, и всегда будет существовать, изменяясь лишь внутри себя. В материалистических представлениях вечная и всемогущая материя с её законами сохранения фактически занимает место Бога.

Действительно, если количество энергии во Вселенной есть постоянная величина, которая не уменьшается и не увеличивается, то это как бы подразумевает, что сама Вселенная тоже сохраняется.

Однако радость материалистов от открытия Закона сохранения энергии уместно сравнить с эйфорией, которую испытывали пред отплытием пассажиры «Титаника». За эйфорией не разглядели огромный айсберг, который похоронил все ожидания.

Если количество энергии во Вселенной постоянное, значит, это какая-то конкретная, ограниченная величина. Поскольку масса находится в прямой зависимости от энергии, значит, и масса материи Вселенной ограничена. Учитывая, что время и пространство – это атрибуты материи, ограничение массы материи автоматически означает ограниченность Вселенной в пространстве и времени. А ограниченность во времени означает только одно: Вселенная имеет начало и конец. «Ибо тому, что сотворено, суждено умереть» (К. 23:15).

Глава 10. О количестве энергии во Вселенной

Согласно Большой Советской Энциклопедии, «весь окружающий нас мир представляет собой движущуюся материю».

Обратите внимание: «движущуюся», а не застывшую!

По определению, движение есть форма существования материи. Иными словами, есть движение – есть материя, есть Вселенная. Нет движения – нет материи, нет Вселенной.

А мера движения – это энергия.

Энергия присутствует в любой материальной системе. Иначе просто никакой системы не было бы. Она присутствует, безусловно, и во Вселенной.

Согласно Закону сохранения количество энергии в изолированной системе неизменно, то есть представляет собой некую константу. В каждой изолированной системе эта константа имеет какое-то определенное значение. Но нас интересует не любая изолированная система, а одна конкретная – Вселенная.

И, коль скоро, согласно Закону сохранения, количество энергии во Вселенной представляет собой постоянную и неизменную величину, мы вправе ожидать, что ученые назовут нам эту величину.

Но не тут-то было. Они не спешат этого делать. И вообще предпочитают обходить вопрос стороной, отделываясь невнятными комментариями.

Столетием назад закрыть этот неудобный вопрос было проще. В те времена еще господствовало представление о стационарной Вселенной, вечной и бесконечной. «А значит, и количество энергии в ней бесконечно», – отвечали тогда навязчивым интересующимся. Впрочем, ясности это и тогда не добавляло. Что это за «константа», если она не имеет конкретного значения?

Стационарная модель Вселенной давно отправлена на свалку истории. Современная наука убедительно отвергла представление о бесконечности Вселенной. Да, Вселенная велика. Возможно даже она больше, чем мы думаем. Но она не бесконечна. А значит, энергия Вселенной имеет конечное, вполне определенное значение.

Каково это значение?

Поскольку ученые молчат, давайте попытаемся на него ответить сами.

Начнем с шутливой задачки, на которой прокалываются даже серьезные физики.

Представьте себе, что хулиганы привязали к хвосту кошки консервные банки. Известно, что таким образом экипированная кошка производит бешеный шум, который пугает, прежде всего, её саму. От чего она бежит ещё быстрее. Но чем быстрее она бежит – тем больший шум производит.

Вопрос: с какой скоростью должна бежать кошка, чтобы не слышать этого шума?

На ум сразу приходит сверхзвуковая скорость – если разогнать кошку до такой скорости, она не будет слышать производимого ею шума, потому что он будет запаздывать, распространяясь с меньшей скоростью.

А ведь есть и другое, более простое и естественное решение этой задачи.

Чтобы не слышать шума кошка… не должна бежать! Или, если угодно, ее скорость должна быть равна нулю.

Эта шутка – прямая аналогия нашей проблемы.

Когда говорят о том, что количество энергии в изолированной системе есть величина постоянная, это не обязательно означает, что такой системе присуще какое-то определённое количество энергии. Это количество может иметь и нулевое значение. Закону сохранения энергии такое решение не противоречит. Закон ведь требует только неизменности количества энергии, но не утверждает, что это количество должно быть обязательно ненулевым.

Не противоречит ли такой вывод реальности? Ведь система с нулевой энергией, как уже говорилось выше – это мертвая система, не способная совершать работу. А Вселенная живет и находится в движении. Может ли при этом ее совокупная энергия быть нулевой?

Да, может!

Этот парадоксальный вывод подтверждается научными данными.

Бенджамин Франклин

В 1747 г. американский физик Бенджамин Франклин, тот самый, чей портрет красуется на стодолларовой купюре, открыл еще один закон сохранения – закон сохранения электрического заряда. Закон постулирует точное равенство скалярных величин положительного и отрицательного элементарных зарядов. Звучит это так: «Алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему17, не изменяется при любых процессах, происходящих в этой системе». В 1843 закон сохранения электрического заряда был экспериментально подтвержден Майклом Фарадеем.

Оказалось, что разноименные заряды (заряженные частицы) появляются и исчезают парами: положительные и отрицательные. Каково бы ни было их количество, в сумме они дают ноль.

Макроскопические (то есть большие) тела, как правило, электрически нейтральны. В них в равных количествах содержатся как положительные, так и отрицательные заряды. Если говорить о Вселенной, то, как считают ученые, её полный электрический заряд равен нулю. Количество положительных зарядов во Вселенной равно количеству отрицательных.

Это касается не только электрических явлений, но и механических. Открытый Уоллисом закон сохранения количества движения также допускает нулевое значение общего (суммарного) количества движения в изолированной системе. Силы взаимодействия тел, составляющих систему, должны быть взаимно уравновешены, в соответствии с Третьим законом Ньютона: «действие равно противодействию».

И в Законе сохранения количества движения, и в Законе сохранения заряда константы равны нулю.

Почему с Законом сохранения энергии, частными случаями которого являются законы Франклина и Уоллиса, дело должно обстоять иначе?

Несложно представить себе систему, состоящую из многих взаимодействующих (движущихся в разных направлениях) тел, даже такую большую, как Вселенная, в которой моменты взаимодействующих между собой тел взаимно погашаются и их результирующая сумма равна нулю.

Эти соображения позволяют предположить, что, хотя в отдельно взятой части системы количество энергии может достигать весьма значительных величин, скалярная сумма всей энергии Вселенной равна нулю.

Похоже, это единственное удовлетворительное решение для величины энергетической константы Вселенной.

Выходит, дело обстоит следующим образом:

– когда не было Вселенной – энергия была равна нулю;

– когда появилась Вселенная, в ней возникли взаимно уравновешивающие друг друга силы и разнонаправленные движения. Но их результирующая сумма продолжает оставаться нулевой;

– когда, исчерпав свою энергию и способность к движению, материя исчезнет – ее совокупная энергия по-прежнему, в соответствии с Законом сохранения, будет равна нулю.

С точки зрения Закона сохранения энергии нет никакой разницы между существованием или несуществованием Вселенной: Закон не нарушается как в том, так и в другом случае.

Иными словами, Закон сохранения энергии не подтверждает убеждение материалистов насчет вечности и неуничтожимости материи. Совсем наоборот, из этого закона следует, что Вселенная не вечна, что у нее было начало и будет конец.

Но вернемся к генеральной линии нашего рассуждения. Нам осталось познакомиться со Вторым началом термодинамики.

Глава 11. Второе начало термодинамики

Незнание второго начала термодинамики равносильно незнанию произведений Шекспира.

Чарльз Сноу

Если Первое начало термодинамики говорит, что все процессы в изолированной системе приводят к ее переходу в неактивное состояние, в Хаос, то Второе начало утверждает, что сама собой система выйти из коматозного состояния не способна.

Для наглядности рассмотрим два простых примера.

Пример первый. В двух сообщающихся сосудах налита вода. Уровни воды в обоих сосудах одинаковы (так всегда бывает в сообщающихся сосудах).

Возможно ли, чтобы уровни воды в сосудах сами собой (без всякого внешнего воздействия) вдруг изменились? Чтобы в одном из сосудов уровень воды поднялся, а в другом опустился, то есть возникла бы разность потенциалов, обеспечивающая возможность совершения работы?

Пример второй. У нас есть один достаточно большой сосуд с водой. Плотность воды одинакова по всему объему сосуда и составляет 1 г/см3, что подтверждает помещенный в воду ареометр.

Возможно ли, чтобы без всякого внешнего воздействия в каком-то месте сосуда вода вдруг приобрела большую или меньшую плотность. Например, ее плотность в одном месте сосуда стала бы 1,2 г/см3,а в другом – 0,8 г/см3?

Ответ представляется очевидным: конечно, ни то, ни другое – невозможно!

Таких событий еще никто никогда не наблюдал.

Правда, невозможность первого и второго событий – разная.

В первом случае она носит безусловный характер, а во втором – вероятностный.

В чем разница?

Разница в том, что в первом случае мы имеем дело с макрообъектом, в данном случае – с жидкостью, поведение которой предсказуемо, и мы точно знаем, чего можно от нее ожидать. Во втором случае приходится иметь дело с поведением частиц, составляющих вещество, предсказать поведение каждой из которых невозможно. Тут мы можем говорить лишь о вероятности того, где каждая из этих частиц окажется в тот или иной момент времени.

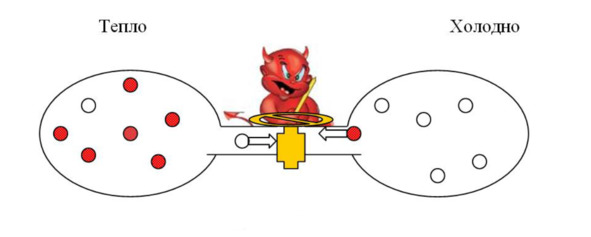
Когда речь заходит о Втором начале термодинамики, обычно приводят такой пример. Представьте себе изолированную систему, состоящую из двух сосудов, соединенных трубкой. Сосуды заполнены каким-нибудь газом, да хоть обычным воздухом, который, само собой, равномерно распределяется по всему предоставленному ему объему. Как сделать так, чтобы в одном сосуде воздух нагрелся, а в другом охладился? Не прибегая, естественно, к внешним воздействиям.

Вспомним, что температура физического тела (и газа тоже) определяется интенсивностью колебаний составляющих его частиц. Чем быстрее движутся частицы, тем выше температура (и ниже плотность). При любой исходной температуре в газе имеются частицы, колеблющиеся с разной скоростью. Вот если бы мы могли разделить их: медленные – налево, быстрые – направо… Тогда между сосудами возникла бы разница температур. Но как это сделать?

С точки зрения теории вероятностей, если сидеть у таких сосудов очень долго, очень – очень долго, века, тысячелетия, миллионы, а может быть и миллиарды лет, или еще дольше, то однажды произойдет чудо, и все быстрые частицы соберутся в одном сосуде, а медленные – в другом.

Можно этому верить, можно нет.

Вот, у Максвелла, например, не хватило терпения: он предложил на трубке, соединяющей сосуды, установить кран и посадить у крана демона, который бы в одну сторону пропускал только быстрые частицы, а в другую – только медленные. Этот неутомимый демон вошел в учебники под названием «демон Максвелла».

Демон Максвелла

В жизни таких демонов не бывает. А потому и самопроизвольного возникновения разности потенциалов в изолированной системе не бывает тоже.

На практике Второе начало термодинамики означает, что равномерное, равновесное состояние изолированной системы является наиболее вероятным, и поэтому система всегда, в любой момент времени, стремится это состояние сохранить.

Совместное действие Первого и Второго начал термодинамики на изолированную систему выражает Закон возрастания энтропии, который можно сформулировать следующим образом: «В изолированной термодинамической системе энтропия не может убывать. Она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс».

В соответствии с этим законом реальная изолированная система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия.

А когда такое равновесие наступило, выйти из него (перейти в неравновесное состояние) система сама уже не способна.

Применительно к Вселенной это означает, что самостоятельно вывести себя из состояния с максимальной энтропией и нулевой энергией, то есть из «неактивного» состояния Вселенная не может. Это все равно, что пытаться вытащить самого себя из болота за волосы.

Глава 12. Гипотеза флюктуаций

Люди видят то, что хотят видеть; слышат то, что хотят слышать; верят в то, во что хотят верить и отказываются верить в то, что им не нравится.

Скилеф18

Поклонники всемогущей Материи говорят:

– Ну и что, что в начальный момент Вселенная была лишена энергии и обладала максимумом энтропии. Она могла выйти из этого состояния благодаря «флюктуациям»!

Может быть они правы, и существует способ обойти действия законов Природы, запрещающих самопроизвольное возникновение Вселенной? Если такой способ есть, мы должны его узнать.

Флюктуациями (от лат. fluctuatio – колебание) называются «случайные отклонения от средних значений физических величин в системе, состоящей из большого числа частиц».

Обратите внимание: случайные отклонения. Это значит, что с точки зрения гипотезы флюктуаций в основе создания мира лежит не закономерность, а случайность!

В системе с большим количеством частиц, утверждает эта гипотеза, существует вероятность временного локального повышения плотности, т.е. вероятность случайного скопления частиц в одной области пространства.

Шекспир однажды образно назвал людей «пузырями земли». Видимо, он представлял себе, что как в бродильном чане из жидкости появляются, увеличиваются, а затем лопаются и возвращаются назад в ту же жидкость пузыри, так и люди рождаются из земли, а затем вновь возвращаются в неё.

Флюктуационная гипотеза рассматривает Вселенную тоже в виде своеобразного пузыря, спонтанно возникшего в исходной неактивной материальной среде.

Авторы этой гипотезы воспользовались единственным шансом, предоставленным Вторым началом термодинамики, а именно – вероятностным характером этого закона. Второе начало формально не запрещает самопроизвольное уменьшение энтропии в локальной области системы, а лишь констатирует чрезвычайно малую вероятность такого события. Вот за эту малую вероятность и уцепились материалисты. Больше просто не за что.

Предположим, материалисты правы и чрезвычайно маловероятное событие каким-то чудом все-таки свершилось, и в небольшой локальной области системы возникла флюктуация – кратковременное повышение плотности среды, случайное скопление частиц в одном месте.

Барон Мюнхгаузен вытягивает себя за волосы из болота.

Но ведь любая флуктуация довольно скоро заканчивается («рассасывается») и система возвращается к первоначальному, гораздо более вероятному, состоянию!

Временное повышение плотности частиц в каком-то месте системы вовсе не означает, что эти частицы сами собой начнут создавать структуры возрастающей сложности.

Нет ни одной причины, по которой они стали бы это делать.

Зато имеется гораздо больше причин для того, чтобы они вновь рассредоточились, что означало бы конец флюктуации.

Например, какой бы большой объем чистой воды вы не взяли, вряд ли в нём сами собой образуются рыбы или хотя бы амебы, хотя в некоторых местах этого объема в течение бесконечно большого временного промежутка плотность воды и может ненадолго самопроизвольно увеличиться. Это случайное уплотнение, однако, долго не продержится: оно будет стремиться к наиболее вероятному состоянию, то есть состоянию с наибольшей энтропией. Достаточно просто представить судьбу очень – очень маловероятной флюктуации на фоне стремления объемлющей её среды перейти в состояние с максимальной энтропией.

Можно ли принимать такое случайное и кратковременное явление за причину возникновения столь огромного и сложнейшего механизма, как Вселенная?

Ответ очевиден. Сценарий, предусматриваемый флюктуационной гипотезой, нереалистичен и не подтверждается практикой. Флюктуационная гипотеза – это соломинка, брошенная утопающему материализму в тщетной попытке его спасти.