Mathematics of the market. Problem book

Mathematics of the market

Problem book

Alexander Berlin

© Alexander Berlin, 2019

ISBN 978-5-4490-5249-0

Created with Ridero smart publishing system

Acronyms

A Relative- relative consumption.

Areal real consumption.

Amax-maximum possible consumption.

A serv (t1, t 2) = serviced supply of batch n in the interval of

time (t1, t2)

Aincoming. (t1,t2) — incoming supply goods for a period of time (t1, t2)

Alost (t1, t2) – losses of demand on market during

time interval (t1, t2)

a – specific weight relative consumption

a (Engset formula) – mathematical expectation and intensity of the

batches of goods from a single source

ci – average volume of one purchase (units) in one moment of time.

Cdelay– average queue length (average number of detained batch of goods)

Closs – losses requests;

Crequest- received requests.

E1,n (A) – value of loss for the consumer system, numerical table values for the first Erlang formula.

E2, n (A) – value of loss for the consumer system, numerical table values for the second Erlang formula.

P request, – losses in the number of requests received for supply of goods,

P goods – the losses in volume of the goods,

Pt. – the losses the time of realization

p (γ> 0) — probability that the waiting time is greater than zero

p (γ> t) – probability that the waiting time of incoming batch of goods anymore t.

Pqueue – probability of having a queue of at least one consignment, the probability of the queue n

p (R> r) – probability that a length of a queue is greater of given value r

tconsum-average duration of consumption for consumers

TGD. The time of greatest demand

α- parameter of the flow of batches of goods in a free state

β – duration of product consumption

γ‘- average waiting time for batch of goods incoming on the market.

γ ̅delay — average waiting time of batch of goods the queue.

λ s (t) -а parameter primitive flows

Introduction

This book supplements the theoretical principles already published in books [1.1].

It studies the issues that arise at various stages of functioning of the market and offers their solutions by using methods of the mass service theory. The application of the proposed mathematical methods enables rigorous calculations of the desired parameters.

At the initial stage of introduction of goods in the market arise questions.

1. The value of the demand for this product

2. Possible revenues.

3. The reliability of the repayment of the loan (in the case of receipt).

At the stage supply of batch of goods need consider the competition.

1. How affect, the behavior of market competitors (the increase of the supply of goods or their reduction).

2. The effect on the demand the appearance on the market of new competitors.

3. As the influence of external factors (disasters, weather, etc.).

4. The pricing policy. Interest rates, money supply.

5. Different properties of the market.

We are considering the properties of the market.

1 Number suppliers.

2. The uniformity of the delivered goods.

3. The dependence of demand on moment of time.

4. The discipline of service of goods – no accumulation of unsold goods or saving their in warehouses

5. Strategy of providers in case of overproduction

The solution of these questions we will consider in the following order.

1. First, we will analyze the proposed mathematical model, which will congestion, determination of the necessary number of buyers

2. We will define what is a product and enter the basic unit of measure that will allow us to analyze any goods.

3. Consider formulas that allow you to determine the characteristics of supply and demand for a given network.

4. Consider examples of solving problems for specific markets (for example, the calculation of the oil market, the prevention of market overload, determining the required number of buyers for a given percentage of losses).

Chapter 1. The initial concept

1.1. A mathematical model of the market

Definitions

For the mathematical evaluation of processes in the economy it is necessary to create a model that would reflect them in mathematical form. In conjunction with the definition of units of measure of supply and demand – relative consumption, this model allows to obtain and to provide a quantitative calculation, analysis and assessment of possible market behavior. The proposed model is shown in Fig.1.1.

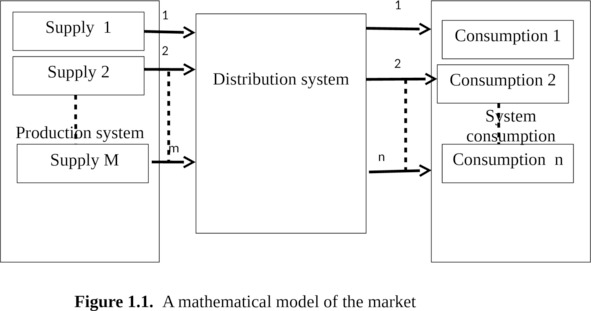
The market contains subsystems that perform the following tasks

Production system – generates random flows of goods (in general case different from each other). Under the goods refers to any product or service offered for sale, in which there is a need (in the following we will show how to define the demand in numerical form). These can be food items, for example, as milk and other food products, cars, homes, cleaning services house, stocks, a construction company offering services in construction of houses, etc.

Flows enter the distribution system.

The distribution system can the request handle immediately or with some delay. The refusal can be of two types:

– the refusal to accept the goods because of lack of demand;

– or installation on waiting of implementation (accumulation of goods)

There are two types of distribution systems.

First type performs the task as quickly as possible to sell the goods without any additional conditions. In queuing theory, such a system mass service is called “full accessibility system” because it provides equal access to the system of consumption, and this system can be not taking into account for calculation of behavior of the market.

Systems of the second type, distribute the goods, given the specified priorities and limitations for individual consumers or consumption. For example, the sale of tobacco, alcohol, weapons… systems of this type are called with not full access.

If the order is accepted, the distribution system is trying to give its to consumers to the consumer network

In our model we have included in the distribution system is an important point, which consists in the ability to influence the demand by setting prices (commonly given with the consideration the price of the manufacturer).

The price may limit demand (privileged goods) or stimulate it (discounts, sales, or other action).

Consumption system serves the flow of goods. This is reflected in the fact that individual consumer or group of consumers can buy the offered goods or to refuse from the purchase. Incoming goods can be purchased, any free group of consumers.

If all consumer groups are busy, then the system of consumption is refuses from the purchase of goods, i.e. appear goods losses. State busy – we will name situation when group of consumers, which during the observed period of time, has acquired the maximum possible the quantity of goods and withdrew for some time from consumption.

Not purchased the product can be not offer, for example, to destroy – it named obvious losses. This type market are named a system with obvious losses.

Distribution system can put the product to the queue of waiting for the realization (for the accumulation and, storage of products). This type market is named a system with waiting.

In this case it is important to know the waiting time. It may exceed a reasonable time (the assigned waiting time). In this case we speak of conditional losses. Since the goods available for sale and after a certain time is removed from storage in accordance with agreed terms and conditions.

If the share of refusals of the goods received exceeds a certain number, it indicates overproduction, and requires measures to eliminate such losses.

1.2. Relative consumption. The unit of measure of supply and demand

In order to apply the methods of Queuing theory to the calculation of the basic economic processes, it is necessary to solve one of the key issues of the economy – to determine the product unit measures supply and demand (A-relative consumption).

Let’s start with a quote of Keynes [3.1].

“The difficulties that most bothered me at process writing this book, and I couldn’t clearly articulate their thoughts;

first, the choice of units measurements, suitable for research of economic system as a whole;…”.

“That the units, in terms of which economists commonly work, are unsatisfactory can be illustrated by the concepts of the national dividend, the stock of real capital and the general price-level:”

“The community’s output of goods and services is a non-homogeneous complex which cannot be measured, strictly speaking, except in certain special cases, as for example when all the items of one output are included in the same proportions in another output”.

We will try to find an indicator of demand. Let’s call it the relative consumption. – A Relative

He can to acquire the following extreme values.

If the consumer has satisfied his need for this product, P Relative =1,

If the consumer is just starting to buy a goods P Relative l=0.

Let’s is use your experience.

Do you love cakes? I will sell them to you. You will buy them and will desire buy more. I’m going to sell more and more. Finally, you will begin to eat 10 cakes a day. And I offer you still. You say, “Enough!”

I suggest to You free of charge for 12 cakes a day, and You ungrateful saying “No!”. Moreover, buying cakes, You will some time to consume them, and not buy a new one.

What is it? It is the overproduction!

So the current state of the user can be reflected by the value of the relative consumption

0 ≤ P reliative ≤ 1

Let’s continue the search for the mathematical determination of relative consumption.

Introduce the unit (let’s call it a) that will allow us to measure supply and demand “relative consumption”.

It is the ratio of real consumption Areal to the maximum possible Amax

It will ratio

Arelative. = Areal/ Amax.=a

For most of the considering cases we can assume that prices Areal and Amax are equal so the relative consumption is a dimensionless quantity.

When determining the maximum consumption, we assume that no material (money, prices) and external factors (season, fashion) do not limit the consumer. Then the maximum consumption in a given period will be equal to Amax.

Maximum consumption can be standardized (for example, by analogy with the consumer basket). However, it should be noted that the maximum consumption may change in time.

For example, the maximum demand for the commodity “money” may increase depending on the achievements or expectations (the promotion) of technological progress.

The actual and maximum consumption expressed in units of the product (pieces, packages, units of money).

If we use this unit we will for measure the demand and supply of goods, by one consumer or one group of consumers, then we will call this index – SPECIFIC WEIGHT RELATIVE CONSUMPTION and we will denote it a.

If we considered the consumption of a group of n consumers (consumer groups), applied the name RELATIVE CONSUMPTION

Arelative= a×n.

In detail, the influence of the processes of functioning of the market for relative consumption (objective, subjective factors, price) considered in [3.1 – 3.3].

Chapter 2. The market as a system with obvious losses. Basic concepts

2.1. A mathematical model of the market as a system with obvious losses

In this Chapter we consider methods for calculating throughput of market with full accessibility in the system with obvious losses.

We will consider a simplified mathematical model shown in Fig.2.1.

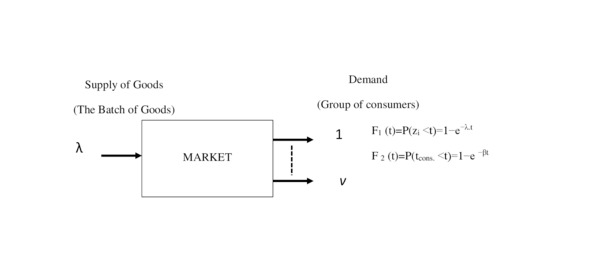
Fig.2.1. Model of the market as a system with obvious losses

In this model, is considered

– the incoming flow of goods, from the system of production

– the flow then enters the distribution system.

– which delivers it into the system of consumption.

The main assumptions which allow to mathematically investigating this process.

Incoming flow:

– consists of identical goods, (this property is named ordinariness)

– result processing of the goods in this moment time does not depend on the results of previous processing (this property is named stationary);

– follow processing of goods the does not depend on the results of previous processing (this property is named the lack of aftereffect).

Random flow, which has all three properties, is called the simplest and well-studied in mass service theory [2.1, 2.2, and 4.3].

The market distribution system

It is assumed that this system has no any stimulating or limiting effect on the service process goods

The system of consumption operates as follows.

The system consists of n groups (or individual) consumers.

Each group receiving a certain amount of goods and after out some time (time of consumption – tconsum) and may be free for further consumption.

For example, a consumer who bought a vehicle, uses it (consumes) for about 3 years, and then begins to look for a new one.

Not to be confused with the time of consumption and time of possession. User has

the old car, but as soon as he begins to look for a new one car – this point is the end point of consumption.

If satisfied demands one of a group of consumption then the number of groups decreases by one, i.e., for consumption remains n-1 group.

At high intensity can be that there will come a time when all n groups of customers will busy.

Whereupon, the received goods will not be sold. Unsold merchandise we will call a LOSSES.

The probability of losses of the goods with a certain number of receipts and number of groups consumption, can give answer one or more questions.

For example,

1. At what size supply, losses will exceed a given norm?

2. What number of goods can processing the market in a given time?

3. How much should be consumer groups to ensure that given quantities of goods were sold with losses less than or equal to the specified norm?

4. What happens to losses if we increase the supply at a certain value? The appearance on the market of new suppliers or an increase in the supply of production.

The answers to these questions can be found by applying the formula of Erlang.

2.2. The first Erlang formula for the calculation of market indicators

The first Erlang formula has the form.

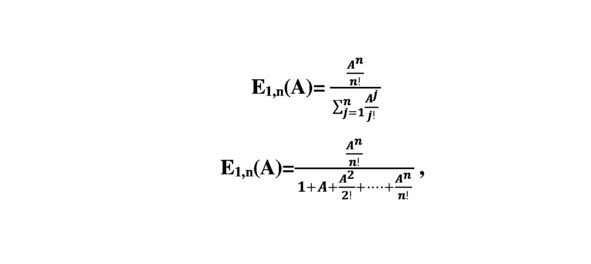
The first Erlang formula

where A is the value proposal, expressed in relative units (see further explanations)

E1,n (A) – value of loss for the consumer system of n groups (the number one indicates that this is the first Erlang formula, then will the area of application of the second formula Erlang).

Chapter 3. Examples of application of the first formula of erlang for solving problems of the market

3.1. Define the initial data

3.1.1 Example 1. Determination of the intensity of consumption

Problem: Structural composition of consumers of products offered on the market is divided into 5 categories n1=50; n2=40; n3=30; n4=20; n5

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.