Начала пространствознания

Здравствуйте, Ребята!

Кто скажет, что такое бублик? Большая баранка! Очень большая сушка! Хлебобулочное изделие с дыркой! Пожалуй, последний ответ самый смешной. Во-первых, вполне достаточно сказать «хлебное изделие». А во-вторых, весьма смешно звучит «с дыркой». Вам, наверняка, приходилось слышать выражение «дырка от бублика».

Можно даже пошутить и сказать, что у двух бубликов две дырки, у трёх ─ три, и так далее. И можно даже шутливо утверждать, что сколько бубликов ─ столько же и дырок. Почему шутливо? Потому, что если утверждать так всерьёз, то это будет совсем неправильно!

Ведь если следовать такому утверждению, то половинка бублика должна иметь, соответственно, половину дырки! А такого вообще не может быть! Или, например, можно попросить родителей разрезать бублик вдоль, или в плоскости бублика, или поперёк плоскости бублика. И в том, и в другом случае получаться две половинки бублика, каждая со своей дыркой!

Да можно и вообще не резать бублики, а можно просто сложить несколько бубликов стопкой, и на всех окажется всего лишь одна дыра!

Вот так мы опровергли утверждение, которое сначала казалось вполне очевидным!

В чём же была ошибка? Ошибочно было считать «дырку» частью бублика. Ведь, по сути, «дырка» ─ это отсутствие серединной части. А отсутствующая часть уже не может быть частью.

То, что мы называли дыркой ─ это сквозное пространство, которое получилось потому, что бублик имеет форму кольца.

А вы знаете, ребята, как пекут бублики? Сейчас, конечно же, на хлебозаводе все делают механические устройства. Люди только следят за правильностью их работы. А вот как бы попробовать сделать бублик «вручную» … Например, взять кусок теста, скатать из него нечто, вроде длинной сосиски, и затем, изогнув эту сосиску кольцом, слепить оба конца…

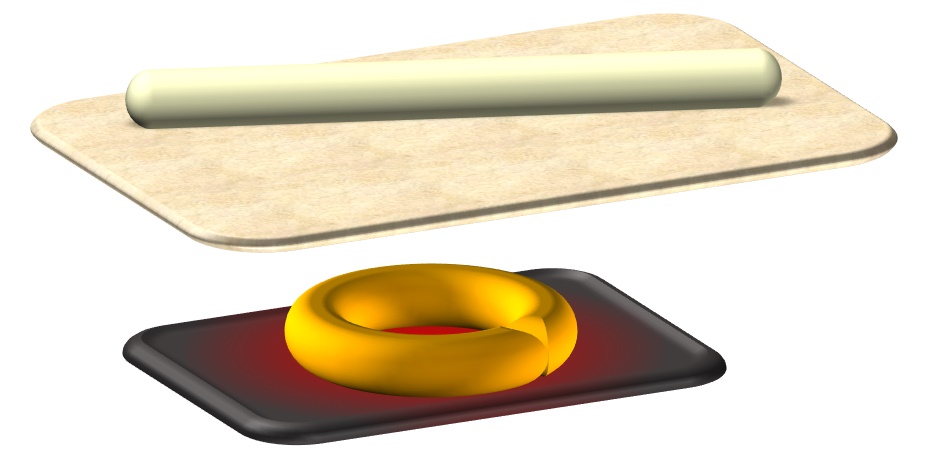
Однако, стык будет заметен, особенно, после выпекания.

Как же пекари делают бублики так, что невозможно определить место стыка? А просто никакого стыка и нет!

Пекарь берёт кусок теста и лепит из него шарик, подобно тому, как мы лепим снежки. Затем, слегка прихлопывает его ладонью, чтобы немного сплющить. Разумеется, что руки пекаря тщательно вымыты и работает он в безупречно чистых перчатках!

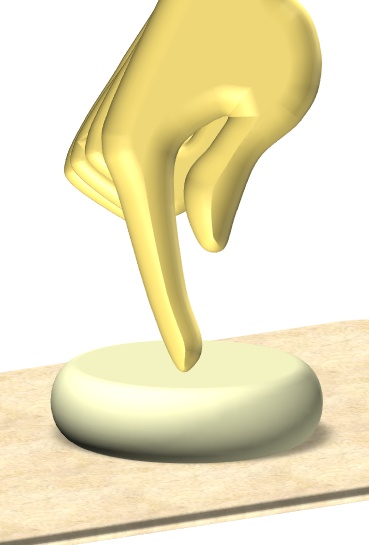
Затем он просто протыкает середину, полученной лепёшки указательным пальцем. Потом, пекарь нанизывает, полученный пончик себе на палец и несколько раз крутит его на пальце, подобно тому, как девочки крутят хулахуп. В результате и получается кольцо без стыков, которое затем выпекается во вкусный и ароматный бублик.

Итак, можно сделать вывод, что кольцо ─ это пространственная форма, которая образует сквозной проём для других пространств.

Следующий вывод, можно сделать вспомнив, как из куска теста можно вылепить или сосиску, или шарик, или лепёшку. И все эти формы не образуют сквозного проёма для других пространств, и их можно назвать сплошными пространствами.

А теперь давайте посмотрим на кусочек сыра. У разных сортов сыра «дырки» разного размера.

Эти «дырки» образуются от того, что, когда сырная масса замешивается, в неё попадает воздух. Пока сырная масса холодная, воздушные пузырьки совсем маленькие. Но когда сыр начинают варить, то воздух, находящийся внутри сырной массы, нагревается, и его частички увеличивают для себя пространство. А уж когда сыр застывает и затвердевает, то расширенные воздушными частичками «дырки» так и остаются в сыре. Но это вовсе и не дырки. Дырками, как мы уже разобрались, называются сквозные проёмы для других пространств. Вот если сыр порезать тонкими ломтиками и полости, образованные пузырьками воздуха, превратятся в сквозные проёмы, тогда их можно будет назвать дырками.

А обратите внимание, ребята, сколько таких вот воздушных полостей, хотя и мелких, в хлебе!

Пространства, которые содержат в себе полости, заполненные другими, пространствами, можно назвать губчатыми, потому что они подобны губке. А сами эти полости можно называть вложенными или внутренними пространствами.

Теперь, зная основные состояния пространств, мы легко сможем легко решить головоломку, которая звучит примерно так:

Вот есть большой ящик, в котором находится коробка, в которой находится шкатулка, в которой находится шарик.

Если шарик находится в шкатулке, которая находится в коробке, которая находится в ящике, то можно смело утверждать, что шарик находится в ящике. Вместо шарика может быть любой предмет, конечно же при условии, что он поместится в шкатулке.

И тогда можно утверждать, что содержимое шкатулки является частью содержимого ящика.

Первый вопрос с подвохом, который могут задать; «Если в шкатулке нет шарика, значит ли это, что шарика нет в ящике?»

На такой вопрос мы уже знаем ответ: «Отсутствующая часть ─ не является частью. А шарик может быть вне шкатулки и в коробке, и в ящике, и вне ящика!»

Второй вопрос с подвохом, который могут задать; «Если в шкатулке ничего нет (пусто), то значит и в ящике ничего нет (пусто). А куда же делись коробка со шкатулкой?»

На такой вопрос мы скажем, что «ничего нет» не бывает! Если есть пространство ─ значит оно чем-то заполнено! Если из шкатулки вынуть шарик, там останется воздух. Если даже воздух откачать, то в шкатулке останется безвоздушное пространство. А это вовсе не пустота, а такое же пространство, как и другие!

Таким образом мы доказали утверждение о том, что содержимое внутреннего пространства, является частью содержимого внешнего пространства.

Чем же мы определяем пространство? Во-первых, конечно же заполненностью. Когда мы говорили о том, как пекут бублики мы упоминали о тесте. В самом простом приготовлении, тесто ─ это смесь муки и воды. Мука ─ это порошок, натёртый из зёрен злаков, а вода, в обычных условиях, это жидкость. Хорошенько смешав эти две составляющих, мы получим тесто. Конечно, для приготовления различных хлебов в тесто добавляют различные вкусовые добавки (соль, сахар, яйцо, масло и тому подобное). Но для нас сейчас важен не вкус, а состояние этого теста. А состояние тесто нельзя назвать ни жидким, ни твёрдым. Тесто обычно даже мягче пластилина!

Скорее всего его состояние можно назвать либо густая жидкость, либо жидкая гуща. Но это ─ пространство! Пока мешали муку с водой туда попало множество воздушных частичек. Но пока мы не станем обращать внимание на примеси воздуха и назовём этот кусок теста сплошным пространством.

Из него можно скатать нечто длинное вроде сосиски, и, при желании, даже ещё длиннее, но тоньше. Можно слепить шарик вроде колобка. А можно расплющить в широкий и тонкий лаваш. Но всё равно, какие бы мы не сделали фигуры, это будет тоже самое пространство, которое занимал кусок теста неопределённой формы.

А вот камни очень твёрдые и попытки изменить их форму приведут только к расколу камня. Все части после раскола будут занимать тоже самое пространство, что и целый камень. Только теперь это будут отдельные пространства! Поэтому, в этом случае, форма пространства не изменилась, но само пространство разделилось.

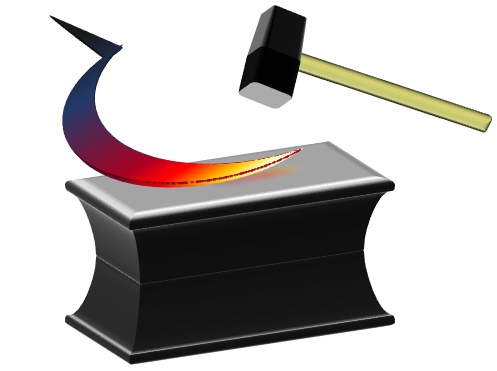
Металлы же можно сильно разогреть и, при помощи молота и наковальни, придавать им другую форму.

Итак, любой предмет, жидкость, воздух и даже безвоздушное пространство является пространством! Некоторые пространства способны изменять форму. Некоторые способны разделяться. Некоторые способны объединяться (воздух и жидкости). Пространства бывают сплошные, с отверстиями и с внутренними полостями.

Если взять обыкновенный ластик (стиральную резинку) и посветить на неё фонариком или лампой спереди, сбоку и сверху, то тени от ластика будут разные. От освещения спереди тень принимает очертания передней части ластика. От освещения сбоку тень принимает очертания боковой части ластика. А от освещения сверху тень принимает очертания верхней части ластика.

Таким образом, осветив ластик с трёх сторон мы получили полную информацию о его форме. Если бы осветили только с двух, то информация была бы неполная. Если бы осветили ещё с какой-нибудь стороны, то информация получилась бы избыточной.

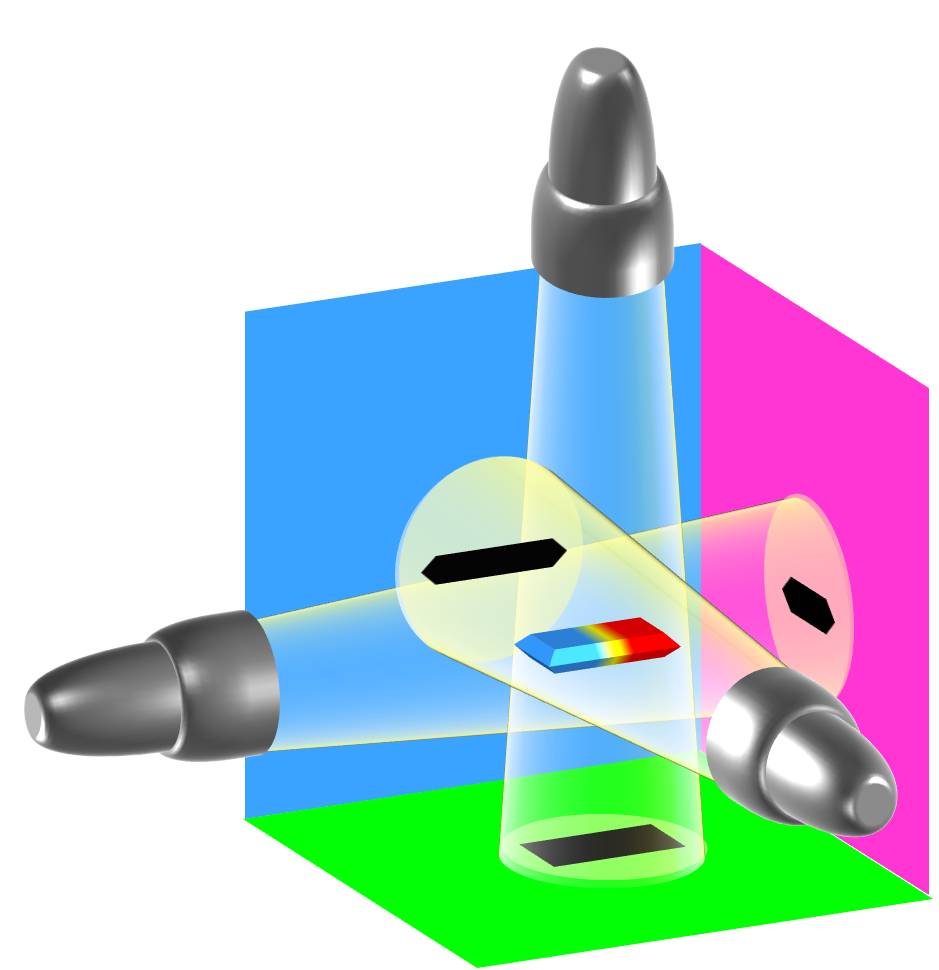
Теперь давайте представим, что зелёная плоскость ─ это нижняя поверхность (пол), синяя плоскость ─ это задняя поверхность (дальняя стена), а розовая плоскость ─ это правая поверхность (боковая стена).

Очевидно, что стыки одной плоскости с другой образуют линию. А стык всех трёх плоскостей образует точку.

Но точки не могут образовывать никаких стыков. А это значит, что точка является окончательным способом состыковки.

Две плоскости на стыке или на пересечении образуют линию. Линия и плоскость на стыке или на пересечении образуют точку. А также линия и линия на стыке или на пересечении образуют точку. Плоскость на стыке или на пересечении с точкой образуют только точку. Линия на стыке или на пересечении с точкой, также, образуют только точку.

Таким образом точка является третьей и завершающей мерой сечения пространства.

А значит пространство ─ трёхмерно и только трёхмерно!

Заметьте, что ни точка, ни линия, ни плоскость не являются ни частями пространства, ни частями друг друга, они являются лишь результатом стыковки или пересечений частей пространства. Поэтому и плоскости, и линии, и точки являются лишь определителями частей пространства!

Теперь, ребята, вы сами можете моделировать различные и многообразные пространства!