Метод. Московский ежегодник трудов из обществоведческих дисциплин. Выпуск 5: Методы изучения взаимозависимостей в обществоведении

Солнечная активность и рождаемость выдающихся людей в 1780–1850 гг. (осреднение с поправкой на линейный тренд, выборка по 67 285 биографий)

Источник: расчет по материалам Wikipedia и данные The Royal Observatory of Belgium.

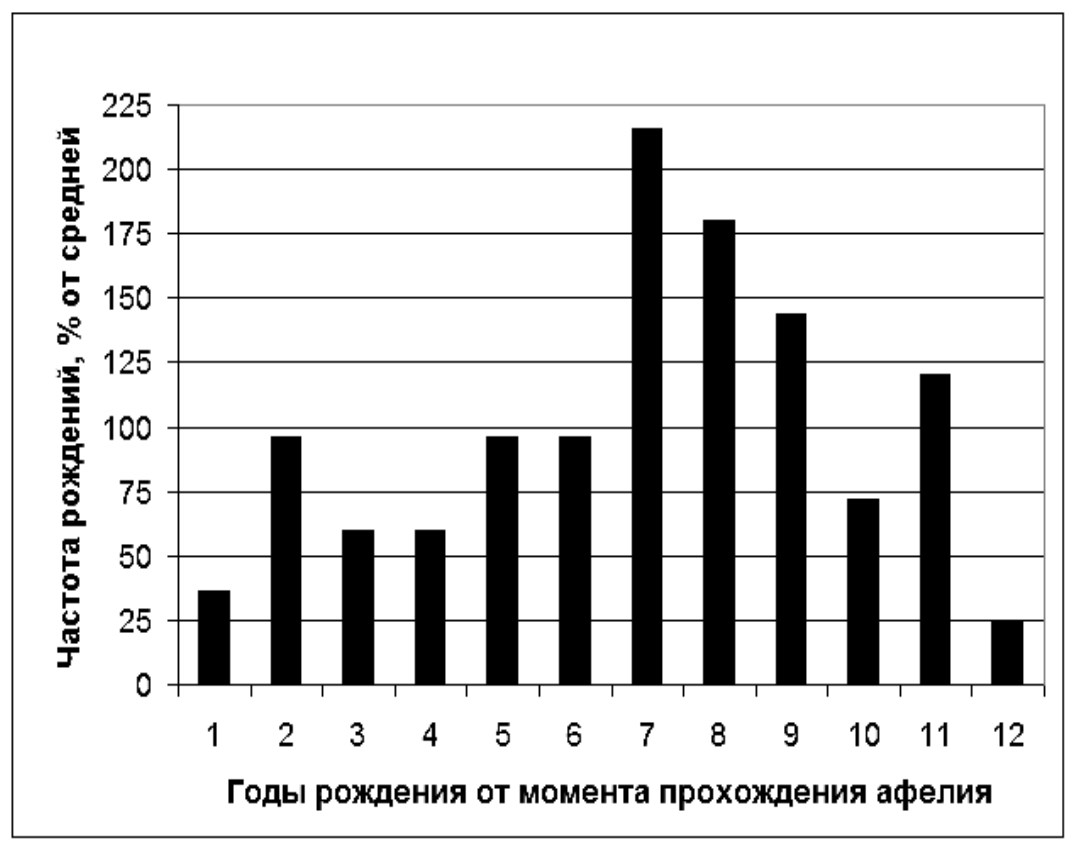
Рис. 6.

Распределение дат рождения национальных поэтов по годам цикла Юпитера (осреднение, выборка по 100 народам мира)

Источник: расчет по материалам Большой советской энциклопедии (2 изд.), Encyclopædia Britannica, Wikipedia, справочников и антологий.

Рис. 7.

Положение планет в июле 2010 г. (условный масштаб)

Источник: расчет по программе Alcyone Ephemeris 3.

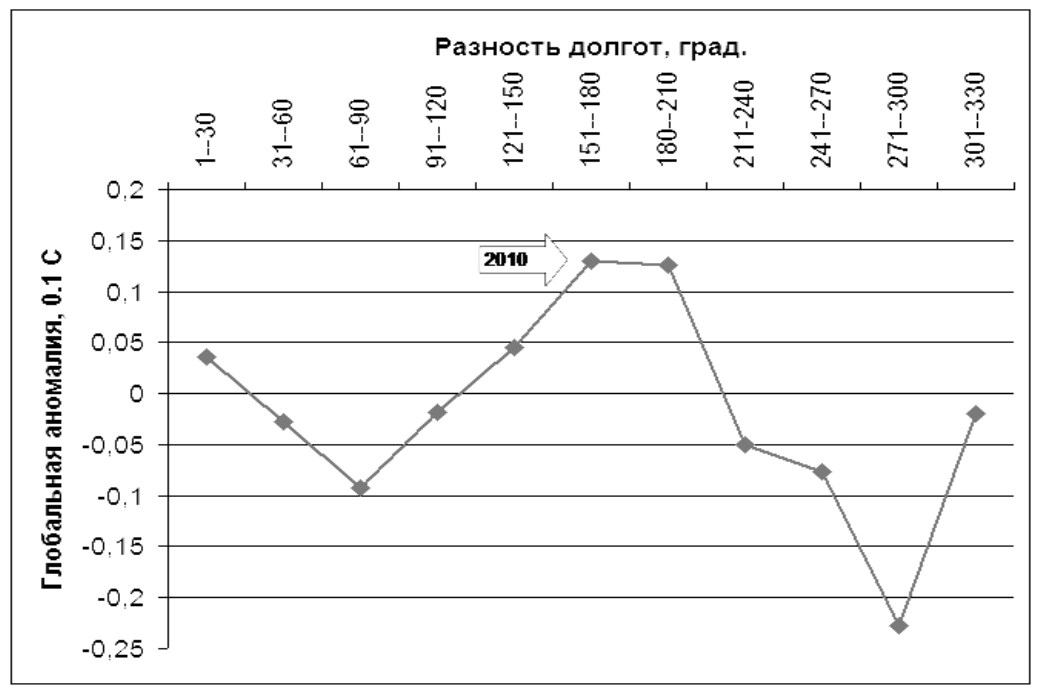
Рис. 8.

Зависимость глобальной месячной аномалии температуры воздуха2 у земли от разности долгот Сатурна и Юпитера в 1880–2012 гг.

Источник: расчет по данным National Climatic Data Center, National Oceanic and Atmospheric Administration с использованием программы Alcyone Ephemeris 3.

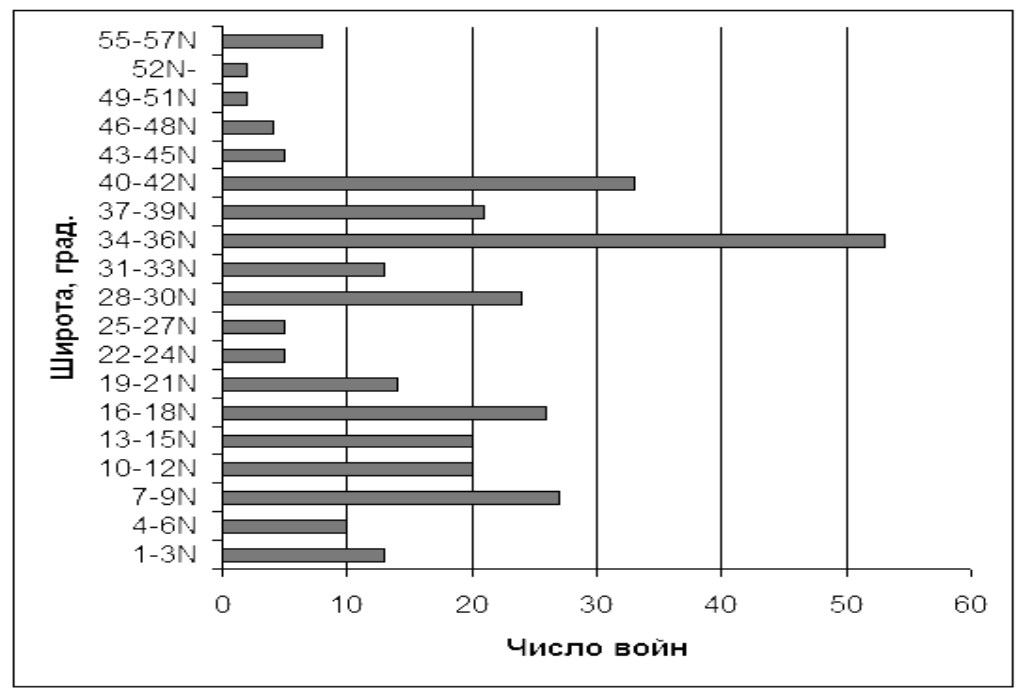
Рис. 9.

Зависимость частоты войн от географической широты3 в Северном полушарии (период 1946–2011 гг., осреднение по 305 событиям)

Источник: расчет по данным The Integrated Network for Societal Conflict Research, The Center for Systemic Peace.

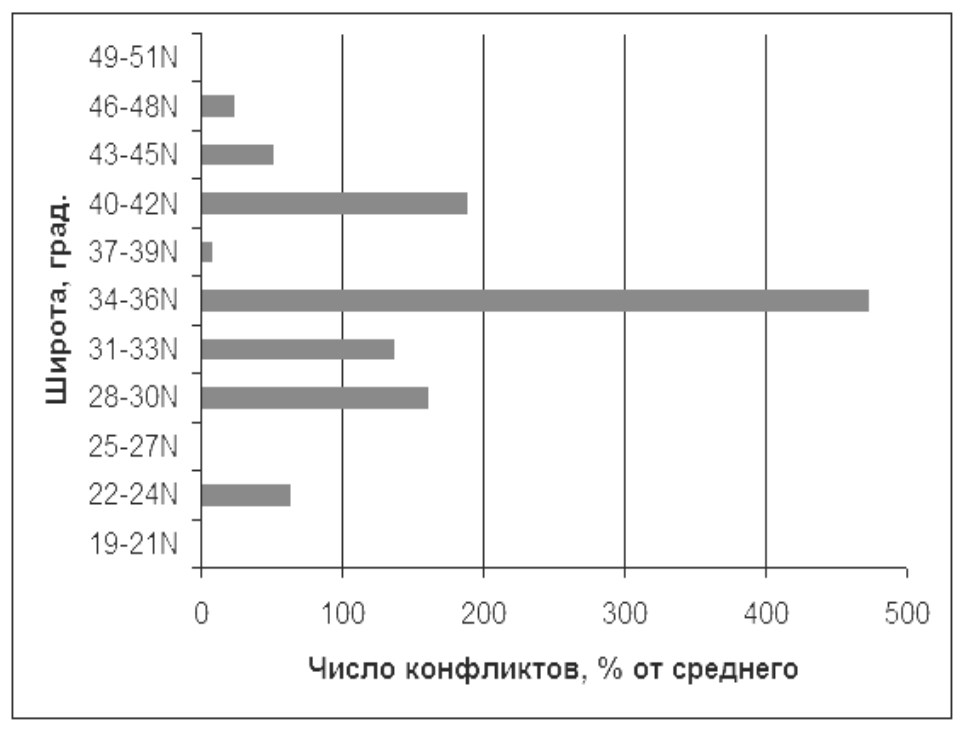
Рис. 10.

Географическое распространение межэтнических вооруженных конфликтов в Северном полушарии (период 1955–2011 гг., осреднение по 282 событиям)

Источник: расчет по данным The Integrated Network for Societal Conflict Research, The Center for Systemic Peace с дополнениями автора.

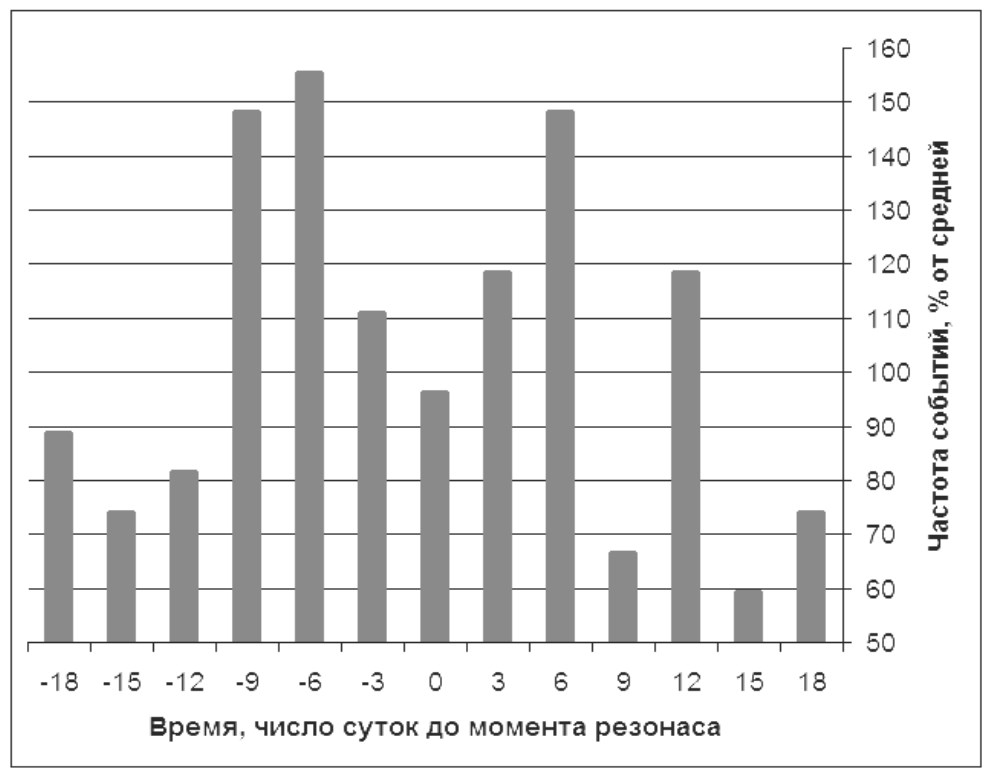
Рис. 11.

Зависимость частоты экстремальных протонных событий от резонанса Меркурия и Венеры 1 : 2 по полуосям орбит (1976–2012 гг., осреднение по 246 событиям)

Источник: расчет по данным Space Weather Prediction Center с использованием программы Alcyone Ephemeris 3.

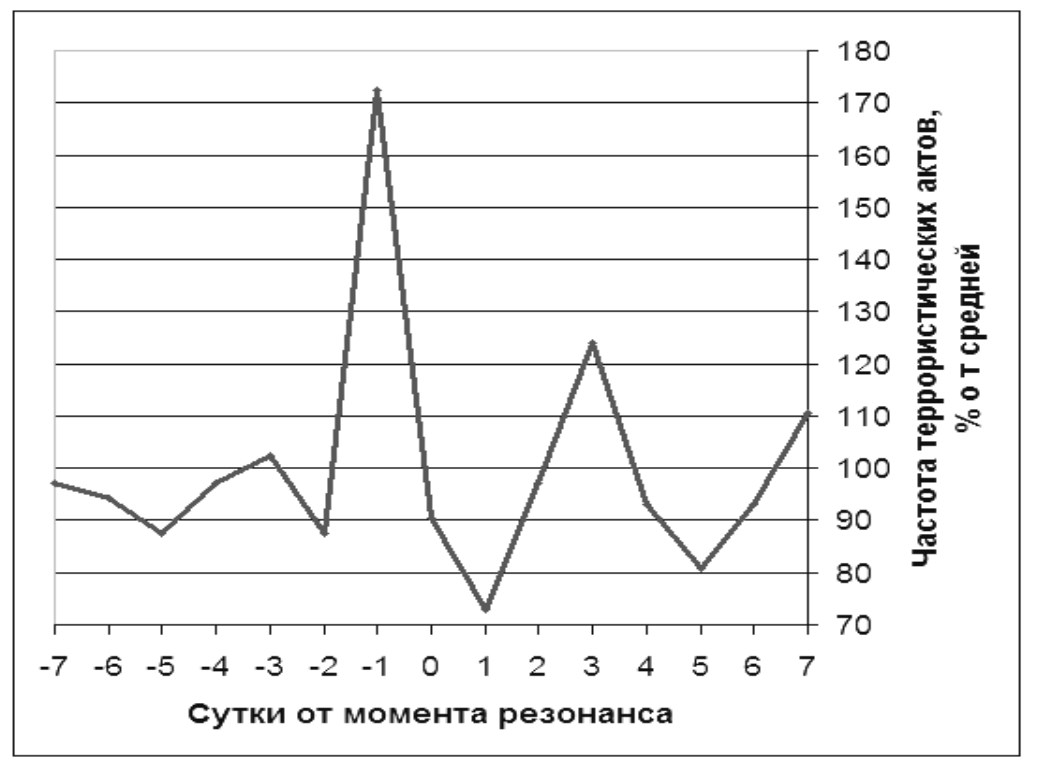
Рис. 12.

Частота террористических актов в Испании в периоды до и после резонанса Меркурия и Венеры 1 : 2 по полуосям орбит (1970–2007 гг., осреднение по 1113 случаев)

Источник: расчет по данным Global Terrorism Database с использованием программы Alcyone Ephemeris 3.

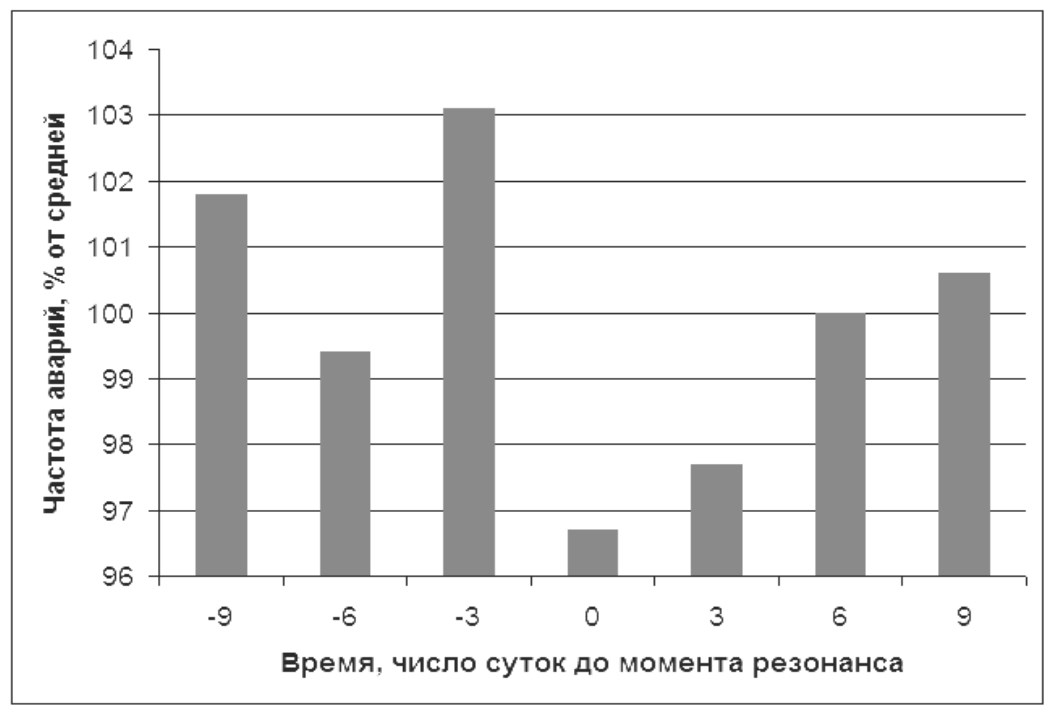
Рис. 13.

Частота автомобильных аварий в Австралии в периоды до и после резонанса Меркурия и Венеры 1 : 2 по полуосям орбит (1989–2012 гг., осреднение с шагом в три дня по 20 257 случаям)

Источник: расчет по данным Australian Road Fatality Statistics с использованием программы Alcyone Ephemeris 3.

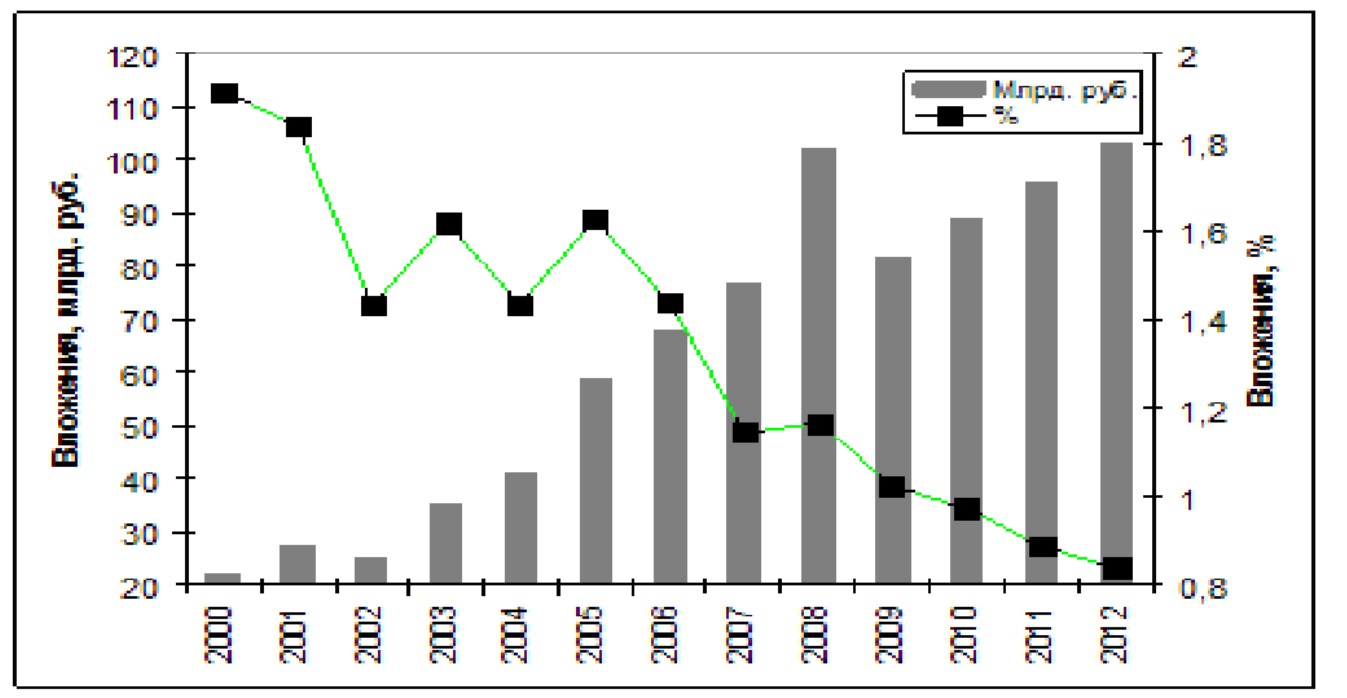
Рис. 14.

Динамика инвестиций в природоохранные мероприятия в Российской Федерации в абсолютном исчислении и в процентах от общего объема капиталовложений

Источник: расчет по данным Росстата.

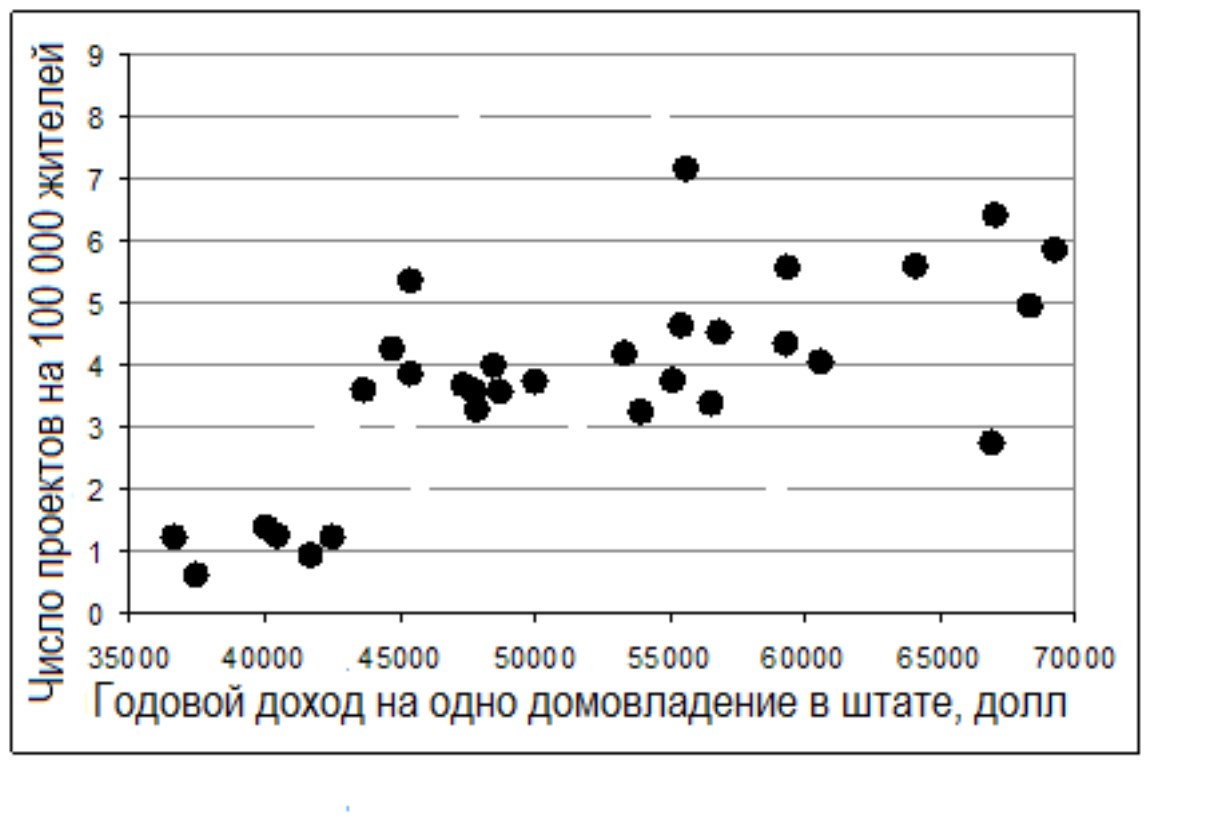
Рис. 15.

Распространение «зеленого» стандарта LEED в США в зависимости от медианного дохода населения (2011 г.)

Источник: расчет по данным US Green Building Council и U.S. Census Bureau.

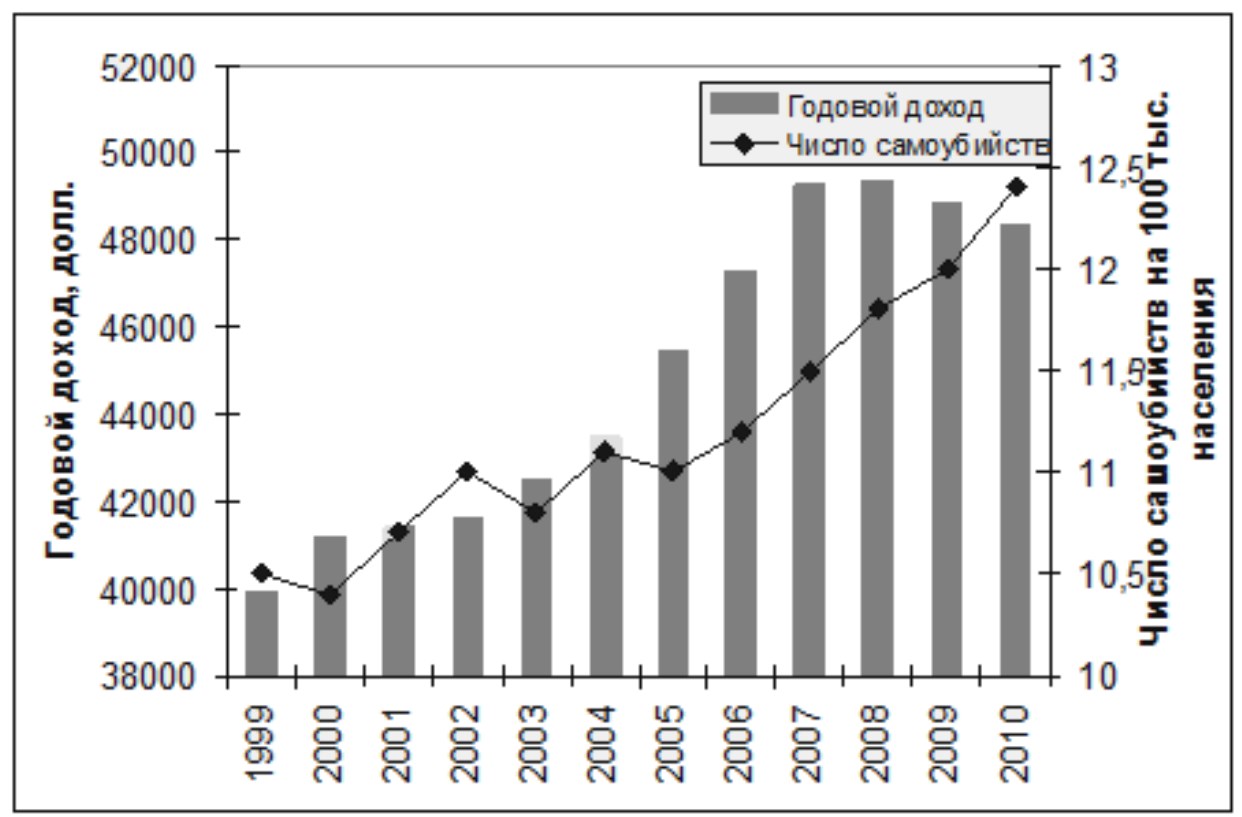
Рис. 16.

Годовые доходы и суицид в США

Источник: по данным American Foundation for Suicide Prevention и U.S. Census Bureau.

Космология судного дня

A.В. Юров1. Введение

Космология считается одновременно самой романтичной и в то же время самой непрактичной из всех наук. Космолог не занимается разработкой новых типов полупроводников, использование которых может привести к новому рывку в области высоких технологий, он не развивает методы интегрирования уравнений газодинамики, что важно для построения новых ракетных двигателей или уточнения метеорологических прогнозов. Космолог не разрабатывает ионные ловушки, алгоритмы квантовых вычислений. Не занимается проблемой термоядерного синтеза и поиском альтернативных источников энергии. Словом, космолог изучает настолько фундаментальные вопросы, что об их практическом приложении говорить вообще не приходится.

Даже деятельность астрономов, людей традиционно далеких от «повседневных проблем», и та выглядит более «земной». В самом деле, именно астрономы наблюдают за движением искусственных спутников Земли, проводящих важные геофизические наблюдения из космоса и обеспечивающих возможность дальней связи. Астрономы должны предупредить нас о возможности падения на Землю крупного астероида, способного нанести существенный ущерб (вплоть до полного уничтожения) человеческой цивилизации. Маловероятность этого события не отменяет необходимости «постоянной службы неба». Наконец, изучение новых и сверхновых звезд совместно с наблюдениями за поверхностью Солнца (с одновременной разработкой математических моделей, описывающих многообразие процессов, происходящих под поверхностью Солнца) призвано привести нас в состояние «боевой готовности» при первых проявлениях того, что Солнце готовится стать новой4.

В отличие от астрономов, космологи исследует вселенную на максимально больших расстояниях. Их интересует то, что происходило 15 млрд лет назад и что произойдет через, по крайней мере, такой же промежуток времени. Их не интересует что‐то меньшее, чем 200 Мпс. Изучая раннюю вселенную, космологи поняли, что им необходима физика очень больших энергий (1017 – 1019 ГэВ), которые, вероятно, никогда не будут доступны в лаборатории. Интересно отметить, что последний аргумент в пользу кажущейся «непрактичности» космологии ряд авторов пытаются обратить в свою противоположность. Дело в том, что область столь высоких энергий представляет особый интерес для специалистов по теории струн. Уже давно было очевидно, что построить теорию ранней Вселенной можно, только используя физику элементарных частиц, однако принципиальным моментом, изменившим статус космологии, стало осознание того, что верно и обратное! А именно построить удовлетворительную теорию элементарных частиц, можно лишь используя космологию. Считается, что описание элементарных частиц возможно в рамках теории струн, но большая часть новых явлений, предсказываемых теорией струн (или ее низкоэнергетическими приближениями), происходит при энергетических масштабах, заведомо недоступных современному экспериментатору. С другой стороны, энергии порядка 1019 ГэВ имели место в ранней вселенной, примерно 15 млрд лет назад, причем формирование современной крупномасштабной структуры вселенной сильно зависит от деталей процессов, протекавших в первые доли секунды после Большого взрыва, которые, в свою очередь, определяются теорией струн. Таким образом, астрономические наблюдения (особенно за реликтовым фоном) оказываются единственным известным на сегодня способом экспериментального тестирования, пригодным для специалистов, работающих в теории струн. Тем не менее исследования в области теории струн сами по себе весьма далеки от практических применений, и неизвестно, изменится ли когда-нибудь это положение вещей.

Все вышесказанное свидетельствует о кажущейся «непрактичности» космологии как физической дисциплины. Цель данной работы – опровержение этого утверждения. Мы попытаемся показать, что справедливо прямо обратное суждение: космология является самой практической из всех наук, поскольку, как мы увидим, приводит к выводам, весьма актуальным не только для космологов, но и для всех людей, в том числе далеких от науки. Мы покажем, что если так называемая стандартная космологическая модель (СКМ), о которой иногда говорят как о «космологическом коркодансе», верна, то человеческой цивилизации осталось существовать гораздо меньше, чем это принято думать! Насколько меньше? Речь идет не о миллионах или тысячах лет, а о столетиях или даже, при наиболее экзотичном варианте, десятилетиях! Вероятно, читатель подумает, что авторы занимаются мистификацией. Каким образом изучение вселенной как целого может привести к таким выводам? Поразительно, но может. Именно этой теме посвящена данная работа. Отметим, что предсказания о грядущем «конце света», сделанные на основе чисто статистических аргументов, давно и оживленно обсуждаются в литературе. Появился специальный термин: Аргумент Судного дня (в подлиннике Doomsday argument [Carter, 1983; Leslie, 1990; Gott, 1993; Nielsen, 1989]). Аргумент Doomsday не использовал космологических соображений и подвергался обширной критике. Наиболее ясно эта позиция изложена в статье Олума [Olum, 2002]. Мы, однако, покажем, что критика Олума несправедлива, если принять во внимание СКМ. Более точно, используя аргументацию Олума в рамках «космологического коркоданса», мы неизбежно приходим к справедливости Аргумента Doomsday. Другими словами, Кен Олум доказал справедливость Аргумента Судного дня, хотя и написал свою работу с целью опровержения последнего!

Работа организована следующим образом: во втором разделе мы обсуждаем Аргумент Судного дня и решение, предложенное Олумом для устранения последнего. В третьем разделе мы показываем, что правило подсчета частот в мультиверсе отличается от того, которое использовалось в [Olum, 2002] для решения парадокса Doomsday и, напротив, приводит к справедливости Аргумента Судного дня. В четвертом разделе, используя данные математической демографии и методы, развитые выше, мы оцениваем время наступления «конца света». Даже грубые вычисления свидетельствуют о том, что «конец света» должен наступить в течение ближайших десятилетий. Трудно счесть такое заключение чем‐то непрактичным, не так ли?

2. Аргумент Doomsday

В своей классической постановке Аргумент Doomsday выглядит следующим образом: пусть pS и pL  – вероятности того, что человеческая цивилизация (раса) будет существовать соответственно «недолго» и «долго». Срок существования – не определяется. Все, что нам надо знать, – это то, что в первом случае человечество исчезнет, набрав в «общей сумме» NS когда-либо живших людей, а во втором – NL, причем NL >> NS. Разумеется, эта картина может показаться чрезвычайно упрощенной. Наверное, возможно множество вариантов развития человечества, и нелепо все сводить к двум возможностям. Тем не менее в качестве некоей усредненной картины ее использовать можно. Современный уровень знаний не позволяет вычислить числа pS и pL = 1− pS, но этого и не требуется. Более того, можно даже принять оптимистичный взгляд на вещи и считать, что величина pL по крайней мере не меньше величины pS. Это не изменит конечного результата. Нас будет интересовать условная вероятность p (S|N), которая равна вероятности того, что «я» живу в короткоживущей цивилизации, при условии, что я N-й рожденный человек. Конечно, определить величину N – затруднительно, поскольку непонятно кого считать первым человеком. Но в принципе ясно, что какое бы соглашение относительно первого человека ни было принято, в рамках его число N будет определено.

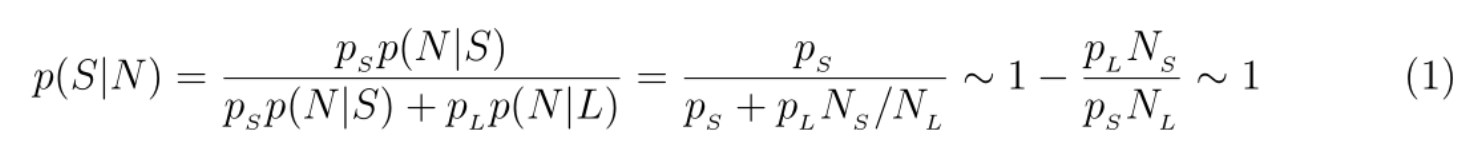
Пусть p (N|S) и p (N|L) условные вероятности того, что я N-й рожденный человек в, соответственно, короткоживущей и долгоживущей расах. Очевидно p (N|S)/p (N|L) = NL/NS. Используя формулу Байеса, находим результат, так как NS/NL << 1. Таким образом, условная вероятность найти себя в короткоживущей расе неожиданно оказывается порядка единицы! Это и есть знаменитый Аргумент Doomsday.

A. Аргумент Doomsday содержит внутреннее противоречие. Представим себе, что несколько десятков тысяч лет назад численность народонаселения составляла в общей сумме (вместе с умершими) 1000 человек. Предположим, что эти люди – фаталисты, уверенные, что грядет конец света, и оценивают общее число всех людей своей расы, вплоть до этого конца в 106. Как мы знаем, сейчас число всех когда-либо живших людей составляет около 60 млрд человек5. Примем, что pS = pL = 0,5. Тогда формула (1) дает

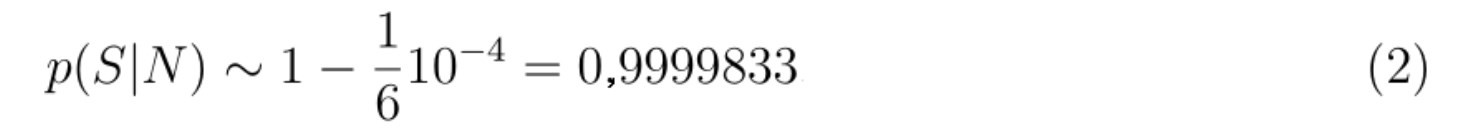
Другими словами, фактически со 100%-ной гарантией эти люди должны были оказаться правы в своих апокалиптических ожиданиях. Вероятность же текущего положения дел (на начало XXI в.) составила бы лишь 0,000017. Тем не менее, как мы знаем, именно это практически невероятное состояние человечества имеет место. Таким образом, древние люди совершили бы огромную ошибку, полагаясь на формулу (1). Но тогда почему мы должны доверять этой формуле?

B. Аргумент Doomsday дает заведомо неправильный ответ. Здравый смысл подсказывает, что вероятность p (S|N) должна быть равна просто pS. Очевидно, где‐то имеется ошибка в вычислениях.

Кен Олум утверждает, что знает где. Вот его рассуждения: для нахождения условной вероятности p (S|N) мы перемножили два числа (опуская нормировочный множитель):

p (S|N) ∼ pS p (N|S), (3)

тогда как правильное выражение имеет вид

p (S|N) ∼ pS p (N|S)NS. (4)

Вводя в (4) нормировочный множитель, имеем

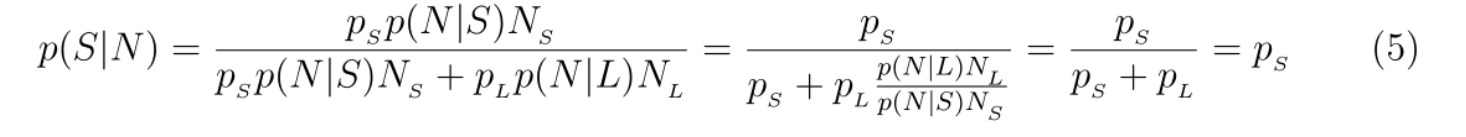
Ответ получается разумным, но почему нам следует использовать предписание (4), а не (3)? Согласно Олуму, для правильного вычисления p (S|N) необходимо перемножить три вероятности: вероятность того, что мы находимся в короткоживущей цивилизации (p S), условную вероятность того, что я N-й человек (p (N|S)), и p (NS|I) – условную вероятность того, что я нахожусь в короткоживущей цивилизации, при условии, что «я есть». Последнее выглядит странно и нуждается в пояснении. Суть дела в том, что сам факт моего существования служит аргументом в пользу того, что я нахожусь в долгоживущей цивилизации, насчитывающей большое число людей. Другими словами, вероятность p (NS|I) должна быть пропорциональна полному числу людей – NS. Для того чтобы сделать этот вопрос максимально ясным, рассмотрим (вслед за Кен Олумом) следующую гипотетическую игровую ситуацию. Пусть некое высшее существо (Олум называет ее богиней) имеет в запасе отель, содержащий 109 одноместных номеров и такое же число людей (одним из которых являюсь я). Богиня бросает монету и в зависимости от того, что выпадает – «орел» или «решка», реализует следующую стратегию.

Стратегия 1.

1.1. Если выпадает «орел», то богиня случайным образом расселяет всех 109 человек по номерам.

1.2. Если выпадает «решка», то богиня случайным образом выбирает 10 человек и наугад расселяет их по первым 10 номерам.

Предположим, что я обнаружил, что нахожусь в одном из первых 10 номеров. С какой вероятностью у богини выпал «орел»? Или иначе, какова вероятность того, что отель полон людей? Эти вопросы имеют прямое отношение к Аргументу Doomsday. В самом деле, результат, полученный по формуле (1), можно объяснить и так: если человечество будет существовать очень долго и полное число всех людей (NL) будет очень велико, то кажется весьма маловероятным найти себя в малой доле людей, живущих у истока цивилизации. Однако мы находим себя в нем, значит, полное число всех когда-либо живших людей, людей, живущих сейчас, и тех, кто будет жить после, не должно быть очень велико. Формула (1) просто дает количественное основание этой идеи. Аналогично в мысленном эксперименте Кен Олума кажется весьма маловероятным, что отель полон, коль скоро мы нашли себя уже в первой десятке номеров. Однако это интуитивно очевидное заключение оказывается неверным. Назовем группу людей, которых богиня будет расселять по номерам реферируемой группой. Теперь предположим, что монета упала «орлом». В этом случае с вероятностью единицы я окажусь в реферируемой группе. Вероятность же того, что богиня поместит меня в один из первых десяти номеров, составит 10−8. Перемножая эти независимые вероятности, я получаю вероятность попасть в первые десять номеров при выпадении «орла», равной 10−8. Если же монета упадет «решкой», то мои шансы попасть в реферируемую группу составят десять к миллиарду, зато вероятность того, что я окажусь в первой десятке номеров, равна, очевидно, 1. Перемножая эти числа, получаем ту же вероятность 10−8, что и при выпадении монеты «орлом». Заметим, что вероятность моего попадания в реферируемую группу и есть величина p (NS|I) (или p (NS|I)). Отношение этих вероятностей в первом и втором случаях составляет один к 10−8, т.е. равно отношению числа членов в реферируемых группах: 109 к 10. Именно поэтому p (NS|I) ∼ NS, а p (NL|I) ∼ NL. Таким образом, вероятность моего попадания в номер, скажем, 7 не зависит от числа людей в отеле и составляет, очевидно, 10–9. В свою очередь это означает, что вероятности выпадения монеты «орлом» или «решкой» равны, а значит, вероятность того, что отель полон, равна 1/2, т.е., возвращаясь к Аргументу Doomsday, p (S|N) = pS. Таким образом, парадокс Судного дня кажется решенным. Но не все так просто!

3. Мультиверс и Doomsday

Свою известную работу [Tegmark, 2003] Макс Тегмарк начинает вопросом, обращенным к читателю: существуют ли другие копии Вас, читающие эти же строки, но принявшие решение оставить чтение, не дойдя до конца данного предложения, тогда как Вы все-таки дочитали его? Люди, живущие на планете, называемой Землей, с горами, среди которых есть Гималаи, с растущими городами (среди которых есть Лондон и Москва)? Люди, живущие в Солнечной системе, содержащей еще восемь планет? Жизнь этих людей совпадает с Вашей во всех отношениях, до того мгновения6, когда Вы приняли решение дочитать первое предложение до конца, решение, свидетельствующее, что Ваша жизнь и жизни этих «копий» стали различаться? Хотя эта картина выглядит странной и невозможной, тем не менее именно ее предсказывает простейшая и наиболее популярная сегодня космологическая модель, причем, согласно этой модели, вышеупомянутые персоны живут в галактике, находящейся приблизительно на расстоянии 10 в степени 1029 метров от нас. Собственно, для обоснования того, что дело обстоит именно так, достаточно принять два обстоятельства: (1) вселенная пространственно бесконечна и (2) она однородно заполнена веществом. Существование вашего alter ego является простым следствием (или предсказанием) так называемой модели конкорданс (concordance), которая находится в согласии со всеми известными астрономическими наблюдениями, расчетами и компьютерными симуляциями. Наибольшее расстояние, которое в принципе можно наблюдать, составляет примерно 14–15 млрд световых лет, поскольку столько лет назад произошел Большой взрыв, послуживший началом нашей вселенной. В сантиметрах это примерно 1028, и сфера с таким радиусом, в центре которой находимся мы, определяет так называемую видимую вселенную, иначе называемую хаббловским объемом. Аналогично вселенная одного из Ваших вышеупомянутых двойников имеет такой же размер, с центром в другой точке и не имеет никакого физического контакта с нашей вселенной. Наша наблюдаемая вселенная оказывается лишь малой частью колоссальной структуры, называемой мультиверсом. Представление о мультиверсе может показаться метафизическим, однако становится все более и более ясным, что существование мультиверса, вытекающее из базовых, по-видимому, неопровержимых физических принципов, может быть эмпирически протестировано или фальсифицировано по Попперу7.

Вернемся к нашим удаленным двойникам. Если пространство бесконечно и распределение материи достаточно однородно на больших масштабах, то даже самые маловероятные события должны где‐то происходить. Недавно Дон Пэйдж показал даже, что если полный четырехмерный объем вселенной превышаетe в степени 1050 см в четвертой степени, то начинают доминировать события с вероятностью, равной спонтанному возникновению наблюдателя-человека [Page, 2005]! На этом фоне уже не удивляет то, что в бесконечной вселенной есть бесконечно много других населенных планет, включая планеты, населенные людьми, обладающими той же внешностью, именем и памятью, что и Вы. Это проистекает из того, что существует множество других областей, того же размера, что и наш хаббловский объем, в которых реализуются все возможные сценарии развития событий! Еще раз подчеркнем, что это является неизбежным следствием простейшей и наиболее общепризнанной современной космологической модели. Действительно, пока все известные наблюдения достаточно уверенно свидетельствуют о том, что мы живем в плоской вселенной, которая, как это следует из уравнений Эйнштейна, ДОЛЖНА быть бесконечной. Колоссальный успех инфляционной космологии служит веским основанием верить, что вселенная и в самом деле бесконечна и плоска, чему, кстати, нас и учили в школе!

Что касается однородности, то наблюдения показывают, что отклонения от средней величины массы, заключенной в сфере радиуса 1023 м, составляет менее 1%, а в сфере радиуса 1027 м отклонение не превышает 0,001%! Таким образом, современные наблюдения однозначно утверждают, что вселенная продолжается и за пределы нашего хаббловского объема, причем там она по-прежнему заполнена галактиками, звездами и планетами.

Есть несколько способов того, как получить отсюда вышеупомянутую «сюрреалистическую» картину вселенной, заполненной нашими двойниками. Первый способ основан на гипотезе эргодичности. Как известно, физическая задача определяется уравнениями динамики и начальными условиями. Согласно современным представлениями начальные условия в ранней вселенной, приведшие к наблюдаемой структуре космоса, были фиксированы квантовыми флуктуациями во время инфляции. Эти флуктуации порождают флуктуации в плотности, которые оказываются эргодически случайными полями. Эргодичность означает, что если вообразить ансамбль вселенных (точнее, хаббловских объемов) со случайно распределенными начальными условиями, то вероятностное распределение исходов в данном объеме совпадает с распределением, полученным случайным выбором объема из всех возможных. Другими словами, при наличии эргодичности все, что может в принципе произойти, на самом деле где‐то происходит.

Более изящен второй способ, предложенный Виленкиным [Garriga, Vilenkin, 2005] и использующий так называемое ограничение Бекенштейна. Суть его сводится к следующему: количество квантовых состояний внутри некоторого объема не может превышать площадь этого объема, умноженную на некоторую постоянную. Строгий вывод ограничения Бекенштейна дается в рамках квантовой теории поля. Однако можно легко (но нестрого!) пояснить, откуда берется это ограничение [Tipler, 2001].

Рассмотрим квантовую, одномерную (для простоты) систему. Неразличимые квантовые состояния лежат в ячейках, меньших, чем произведение неопределенности координаты на неопределенность импульса, поэтому общее число различных квантовых состояний получается делением всего фазового объема на размер такой ячейки. Так как, в соответствии с принципом неопределенности Гейзенберга, размер последней не может быть меньше постоянной Планка, размер полного числа квантовых состояний N не может быть больше фазового объема PR (где P – импульс, а R – координата), деленного на постоянную Планка. На следующем шаге надо вспомнить, что в релятивистской теории импульс P всегда меньше (либо равен – для безмассовых полей) энергии E, деленной на скорость света. Но энергия пропорциональна массе, а значит, число возможных состояний не больше некоторой константы, умноженной на размер исследуемого объема R и на его массу. Наконец, следует учесть, что масса объема при заданном R не может быть сколь угодно велика, ее максимально допустимое значение пропорционально R, поскольку при бoльших массах начнется гравитационный коллапс. Окончательно получаем, что число допустимых, физически различимых квантовых состояний меньше, чем

Ограничение Бекенштейна позволяет понять, откуда берутся «двойники». В силу этого ограничения число начальных условий Nh, приводящих к разным динамическим конфигурациям в заданном хаббловском объеме, – конечно. В [Garriga, Vilenkin, 2001] приведена оценка: Nh ∼ e в степени 10244! Это, безусловно, колоссальное, но КОНЕЧНОЕ число. Таким образом, число всех возможных «историй» внутри данного хаббловского объема – конечно, тогда как число всех хаббловских объемом в бесконечной (ибо плоской) вселенной – бесконечно. Это означает, что если начать перебирать хаббловские объемы один за другим, то рано или поздно мы переберем все объемы с разными историями, после чего начнутся повторения. Другими словами, все возможные истории, все, что могло произойти в нашем мире, но почему‐то не произошло, – где‐то происходит. Кроме того, существует бесконечно много одинаковых миров, буквально совпадающих с нашим, а также миров, лишь чуть-чуть отличающихся от нашего, и т.д. Грубые оценки показывают, что ближайшие к вам ваши же двойники находятся на расстоянии примерно 10 в степени 1029 м от вас. На расстоянии 10 в степени 1091 м располагается сфера радиусом 100 световых лет, такая, что для всех ее обитателей в течение 100 ближайших лет все произойдет в точности как у нас вплоть до 2100 г. Наконец, на расстоянии 10 в степени 10113 м должен располагаться ближайший хаббловский объем, полностью идентичный нашему.