
Полная версия
Математика космоса: Как современная наука расшифровывает Вселенную
Хорошее следствие состоит в том, что после некоторой первоначальной неразберихи молекулы газа начинают вращаться преимущественно в одной плоскости. Первоначально каждая молекула обладает определенным моментом импульса относительно центра тяжести облака. В отличие от волчка газовое облако не имеет жесткой структуры, поэтому скорости и направления движения молекул в нем, вероятно, меняются в широких пределах. Вряд ли все эти величины точно компенсируют друг друга, так что первоначально облако обладает ненулевым суммарным моментом импульса. Из этого следует, что суммарный момент импульса системы обладает каким-то вполне конкретным направлением и имеет вполне конкретную величину. Закон сохранения гласит, что, поскольку газовое облако развивается под действием гравитации, его суммарный момент импульса не меняется. Следовательно, направление оси остается постоянным, жестко зафиксированным в момент формирования облака. И величина момента импульса – общее количество вращения, если так можно выразиться, – тоже остается постоянной. Что в этой системе может меняться, так это распределение газовых молекул. Каждая молекула газа гравитационно притягивает все остальные молекулы, и первоначально хаотичное шарообразное газовое облако стягивается и образует плоский диск, вращающийся вокруг оси, как тарелка на шесте в цирке.
Это хорошая новость для теории Солнечной туманности, потому что все планеты Солнечной системы имеют орбиты, лежащие очень близко к одной и той же плоскости – эклиптике, – и обращаются вокруг Солнца в одном направлении. Именно поэтому астрономы в давние времена догадались, что и Солнце, и планеты сконденсировались из газового облака после того, как это облако сжалось с образованием протопланетного диска.
К несчастью, для этой «небулярной гипотезы» есть и плохие новости: 99 % момента импульса Солнечной системы сосредоточено в планетах, тогда как на долю Солнца приходится лишь 1 %. Хотя Солнце содержит в себе практически всю массу Солнечной системы, вращается оно довольно медленно, а его частицы располагаются относительно близко к центральной оси. Планеты, хотя уступают Солнцу по массе, находятся гораздо дальше и движутся гораздо быстрее – и потому берут на себя почти весь момент импульса.
Однако подробные теоретические расчеты показывают, что коллапсирующее газовое облако так себя не ведет. Солнце поглощает большую часть вещества в облаке, включая и то, что располагалось намного дальше от центра. Поэтому логично было бы ожидать, что центральное светило поглотит и львиную долю момента импульса… чего, как несложно заметить, оно в данном случае не сделало. Тем не менее нынешнее распределение момента импульса, при котором на планеты приходится львиная его доля, прекрасно согласуется с динамикой Солнечной системы. Она работает и работает уже миллиарды лет. Вообще динамика, как таковая, не представляет собой никакой логической проблемы: проблема только в том, с чего это все началось.
* * *Из этой дилеммы был быстро найден один потенциальный выход. Предположим, что Солнце сформировалось первым. Тогда оно действительно поглотило почти весь момент импульса газового облака – ведь оно поглотило и почти весь составлявший его газ. А позже оно могло приобрести и планеты, захватив
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Сноски
1
Mars Odyssey, MRO и MAVEN (США), Mars Express (ЕКА), Mars Orbiter Mission (Индия).
2
Роверы NASA Opportunity и Curiosity. Ровер Spirit перестал функционировать в 2011 году.
3
И ее аналогов в России, Европе и Китае. – Прим. ред.
4
«Эта глупая идея стрелять в Луну – пример того абсурда, до которого порочная специализация может довести ученых. Чтобы вырваться из земного притяжения, снаряду нужна скорость 7 миль в секунду. Тепловая энергия при такой скорости равна 15 180 калорий [на грамм]. Исходя из этого, такое предприятие представляется фундаментально невозможным» – Александер Бикертон, профессор химии, 1926 год
«Я дерзну сказать, что путешествие на Луну силами человека не произойдет никогда, несмотря ни на какие научные достижения» – Ли де Форест, изобретатель электронной лампы, 1957 год.
«Нет никакой надежды реализовать фантастическую идею достичь Луны, потому что барьеры, связанные с необходимостью освобождения от притяжения Земли, непреодолимы» – Форест Моултон, астроном, 1932 год.
5
В редакционной статье 1920 года газета The New York Times писала: «Профессор Годдард… не знает отношения между действием и противодействием и не понимает необходимости иметь что-нибудь получше вакуума, от чего можно было бы оттолкнуться».
Третий закон Ньютона гласит, что каждому действию соответствует равное и противоположно направленное противодействие. Противодействие следует из закона сохранения импульса, и никакой среды, от которой нужно было бы отталкиваться, не требуется. Такая среда только затрудняла бы движение, а не способствовала ему. Справедливости ради отметим, что в 1969 году, когда астронавты Apollo 11 были уже на пути к Луне, газета принесла извинения за эту ошибку. На каждую публикацию найдется равное и противоположное опровержение.
6
Имеется в виду – для своего размера. – Прим. ред.
7
Николя Бурбаки – коллективный псевдоним группы математиков переменного состава (преимущественно французов), образованной в 1935 году и написавшей большую серию книг, в которой авторы попытались заново сформулировать математику на общей и абстрактной основе. Эта работа принесла большую пользу в изучении математики, потому что унифицировала предмет, выделила базовые концепции и привела строгие доказательства. При этом аналогичная философия, получившая название «новая математика» и широко применяющаяся в преподавании школьной математики, не добилась особого успеха и оказалась по меньшей мере противоречивой.
8
В 1726 году Ньютон провел вечер в Лондоне за ужином с Уильямом Стакли. В документе, сохранившемся в архивах Королевского общества и изложенном старинным вычурным слогом, Стакли писал: «После обеда, поскольку погода стояла теплая, мы вышли в сад и сели пить чай в тени какой-то яблони; только я и он. В ходе беседы он, помимо прочего, рассказал мне, что ситуация в точности похожа на ту, в которой он был, когда мысль о гравитации впервые пришла ему в голову. Почему яблоко всегда падает перпендикулярно земле, подумал он… Почему не в сторону и не вверх, а всегда стремится к центру Земли? Очевидно, причина состоит в том, что Земля притягивает его. Вещество должно обладать какой-то притягивающей силой. И сумма притягивающей силы вещества Земли должна находиться в центре Земли, а не где-нибудь сбоку. Итак, падает ли яблоко перпендикулярно или по направлению к центру? Если вещество таким образом притягивает вещество, то это должно происходить пропорционально количеству. Следовательно, яблоко притягивает Землю, точно так же, как Земля притягивает яблоко».
Другие источники тоже подтверждают, что Ньютон рассказывал эту историю, но все это, разумеется, не доказывает ее истинности. Ньютон мог специально ее придумать, чтобы проще было объяснять его идеи. Говорят, что яблоня, с которой упало пресловутое яблоко, сохранилась до сего дня – это яблоня сорта Flower of Kent в усадьбе Вулсторп-мэнор.
9
Если большая полуось эллипса равна a, а малая b, то его фокус располагается на расстоянии

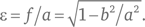
10
Вот как писал об этом сам Ньютон в письме к Ричарду Бентли, написанном в 1692 или 1693 году: «Непостижимо, что неодушевленная Материя может, без Посредничества чего-то еще, что не является материальным, оказывать влияние и действовать на другую материю без обоюдного Контакта… То, что одно тело может действовать на другое на расстоянии через Вакуум, вообще без какого бы то ни было Посредничества… для меня настолько Абсурдно, что я убежден: ни один Человек, имеющий в философских Вопросах компетентные Способности мышления, никогда с этим не согласится».
11
В вакууме. – Прим. ред.
12
Это некоторое упрощение. Запрещено не движение быстрее света, как таковое, запрещен переход через скорость света. Никакой объект из тех, что в настоящий момент движутся медленнее света, не может ускориться так, чтобы двигаться быстрее света; а если вдруг что-то в настоящий момент движется быстрее света, то это что-то не сможет замедлиться и стать медленнее света. Подобные частицы называются тахионами, и на данный момент их существование носит чисто гипотетический характер.
13
В письме к своему другу Конраду Хабихту, датированном 1907 годом, Эйнштейн писал, что думает о «релятивистской теории гравитационного закона, при помощи которой я надеюсь объяснить до сих пор необъяснимое вековое изменение движения перигелия Меркурия». Первые серьезные попытки такого рода были начаты им в 1911 году.
14
В наше время мы соединяем уравнения Эйнштейна в единое тензорное уравнение (из десяти компонент – симметричный четырехмерный тензор), но обычным названием остаются «уравнения поля».
15
Хуже того, скорость хода «бортовых часов» – ультрастабильного генератора частоты навигационного спутника – преднамеренно смещена относительно идеальной примерно на половину миллиардной доли, чтобы получить идеальную синхронизацию с неподвижными часами на поверхности Земли. – Прим. ред.
16
Древнейшие минералы, обнаруженные в метеоритах – современных остатках твердого вещества, сформировавшегося в досолнечной туманности, имеют возраст 4,5682 млрд лет.
17
Книгу эту Декарт написал в 1632–1633 годах, но не спешил публиковать, опасаясь инквизиции. В результате она вышла только после смерти автора.
18
Строгое определение дается через векторы.

