Математика управления капиталом: Методы анализа риска для трейдеров и портфельных менеджеров

Еще одной очень важной синтетической конструкцией, которую мы будем использовать, является концепция единицы. HPR, которые вы будете рассчитывать для отдельных рыночных систем, должны рассчитываться на основе «одной единицы». Другими словами, если это фьючерсные контракты или опционы, то каждая сделка будет основываться на 1 контракте. Если это акции, то вы должны заранее решить, какой будет эта единица: она может равняться 100 акциям или 1 акции. При торговле на спот-рынках или на рынке FOREX вы также должны решить, какой будет единица. Используя результаты, основанные на торговле 1 единицей и применяя методы этой книги, вы сможете получить выходные результаты, основанные на 1 единице, т. е. поймете, какое количество контрактов или акций необходимо использовать в определенной сделке. Не важно, какое количество вы выберете для единицы, так как это гипотетическая конструкция, необходимая только для того, чтобы произвести расчеты. Для каждой рыночной системы вы должны рассчитать, какой будет единица. Например, если вы торгуете на рынке FOREX, то можете выбрать в качестве единицы 1 млн долл. Если вы трейдер на фондовом рынке, то оптимальным числом может быть 100 акций.

И наконец, необходимо решить, будете ли вы торговать дробными единицами. Например, если вы торгуете на товарном рынке и единица равна 1 контракту, то торговать дробными единицами невозможно. Если вы работаете на фондовом рынке и единица равна 1 акции, то также не сможете торговать дробной единицей, однако если 1 единица – это 100 акций, то можно работать с дробной единицей, если есть желание торговать нестандартным лотом.

Если вы торгуете фьючерсами, то можно взять за единицу 1 мини-контракт и не допускать дробных единиц. Теперь допустим, что 2 мини-контракта соответствуют 1 обычному контракту, и с помощью методов, описанных в этой книге, вы приходите к выводу, что надо торговать 9 единицами, – это будет означать, что вам следует торговать 9 мини-контрактами. Так как при делении 9 на 2 получается 4,5, то следует торговать 4 обычными контрактами и 1 мини-контрактом.

Вообще, с точки зрения управления деньгами считается, что торговля дробными единицами дает определенное преимущество, но, как правило, этот выбор не играет большой роли. Посмотрим на двух трейдеров на рынке акций. У одного единица – это 1 акция, и он не может торговать дробными единицами; у другого единица – 100 акций, и он может торговать дробными единицами. Допустим, что сегодня оптимальное количество для первого трейдера составляет 61 единицу (т. е. 61 акцию), а для второго трейдера в тот же день – 0,61 единицы (снова 61 акция).

Многие справедливо полагают: чтобы стать хорошим учителем, нужно довести материал до уровня, на котором он был бы понятен ученику. Один из способов – провести аналогию между концепцией, которую нужно объяснить, и чем-то знакомым. Поэтому в тексте вы найдете много аналогий. Несмотря на то что аналогии могут быть весьма полезны и в споре, и при обучении, я отношусь к ним настороженно, так как они привносят нечто чуждое и вынуждают (часто совершенно несправедливо) рассматривать новую концепцию с точки зрения логики уже известного. Например:

квадратный корень из 6 равен 3, так как квадратный корень из 4 составляет 2, а 2 + 2 будет 4.

Поскольку 3 + 3 = 6, то квадратный корень из 6 должен быть равен 3.

Аналогии объясняют, но они ничего не решают. Наоборот, аналогия делает априорное предположение о том, что некоторое суждение истинно, и это «объяснение» затем считается доказательством. Заранее прошу прощения за использование аналогий в книге: я использую их только для наглядности.

Оптимальное количество для торговли и оптимальное f

Современная теория управления портфелем, возможно, являясь вершиной концепции управления капиталом при торговле акциями, не была принята остальным торговым миром. Фьючерсные трейдеры, чьи технические торговые идеи обычно считаются родственными торговым идеям фондового рынка, не желали принимать методы из мира торговли акциями. Вследствие этого современная теория портфеля никогда в действительности не использовалась фьючерсными трейдерами.

В то время как современная теория портфеля определяет оптимальный вес составляющих портфеля (для достижения наименьшей дисперсии при заданном доходе или наоборот), она не затрагивает идею оптимального количества. Речь идет о том, что для данной рыночной системы есть оптимальное количество, которое можно использовать в торговле при данном уровне баланса счета, чтобы максимизировать геометрический рост. Это количество мы и будем называть оптимальным f. Данная книга предлагает, чтобы современная теория портфеля использовалась трейдерами на любых рынках, а не только на фондовом. Однако мы должны породнить современную теорию портфеля (которая дает нам оптимальный вес) с идеей оптимального количества (оптимальное f), чтобы добиться действительно оптимального портфеля. Именно этот оптимальный портфель может и должен использоваться трейдерами на любых рынках, включая фондовые.

При торговле без заемных средств, т. е. без рычага (например, при управлении портфелем акций), вес и количество – это синонимы, но в ситуации с рычагом (например, при управлении портфелем фьючерсных торговых систем) вес и количество различаются. В этой книге вы познакомитесь с концепцией, которая впервые была освещена в книге «Формулы управления портфелем» и заключается в том, что необходимо знать оптимальное торговое количество, которое является функцией оптимального взвешивания.

Как только мы изменим современную теорию портфеля и отделим вес от количества, то сможем вернуться к торговле акциями с этим теперь уже переработанным инструментом. Мы увидим, как почти любой портфель акций без рычага можно улучшить, превратив его в портфель с рычагом, соединив с безрисковым активом. В дальнейшем все станет интуитивно очевидно. Степень риска (или консервативности) является в таком случае функцией рычага, который трейдер желает применить к своему портфелю. Это означает, что положение данного трейдера в спектре «неприятия риска» зависит не от используемого инструмента, а от рычага, который он выбирает для торговли.

Иными словами, эта книга научит вас управлению риском. Мало кто из трейдеров имеет представление об управлении риском. Это не упразднение риска, поскольку тогда вы целиком упразднили бы выигрыш, и не вопрос максимизации потенциального дохода по отношению к потенциальному риску. Управление риском – это стратегия принятия решений, которая имеет целью максимизировать отношения потенциальной прибыли к потенциальному риску при определенном приемлемом уровне риска.

Чтобы понять это, следует сначала познакомиться с оптимальным f – компонентом уравнения, выражающим оптимальное количество для сделки. Затем следует научиться комбинировать оптимальное f с оптимальным взвешиванием портфеля. Такой портфель будет максимизировать потенциальную прибыль по отношению к потенциальному риску. Сначала мы раскроем эти концепции с эмпирической точки зрения (вкратце повторим книгу «Формулы управления портфелем»), а затем изучим их с более мощной точки зрения, параметрической. В отличие от эмпирического подхода, который использует прошлые данные, параметрический подход использует только прошлые данные и некоторые параметры. Затем эти параметры используются в модели, дающей преимущественно те же ответы, что и эмпирический подход. Сильная сторона параметрического подхода заключается в том, что можно менять значения параметров, чтобы посмотреть, как изменится результат. Эмпирический подход не позволяет этого сделать. Однако эмпирические методы тоже имеют свои сильные стороны. Они в основном проще с точки зрения математики, и их легче использовать на практике. По этой причине в книге сначала рассмотрены эмпирические методы.

В конце нашего исследования мы увидим, как применять эти концепции при заданном пользователем уровне риска, и узнаем стратегии, которые максимизируют рост.

В книге рассмотрено много тем. Я попытался изложить их настолько сжато, насколько возможно. Материал может быть не всегда понятен и, возможно, поднимет больше вопросов, чем даст ответов. Если так оно и есть, значит, я добился одной из целей этой книги.

Большинство книг имеет одно «сердце» – одну центральную концепцию, вокруг которой построена вся книга. Эта книга отличается тем, что у нее несколько концепций. Некоторые посчитают ее трудной, если подсознательно ищут книгу с одним «сердцем». Я не приношу извинений: это не ослабляет логики книги, наоборот, обогащает ее. Чтобы полностью понять материал, изложенный в книге, может быть, вам придется прочитать ее два или даже три раза.

Одной из особенностей книги является более широкая трактовка концепции принятия решений в среде, характеризуемой геометрическими следствиями. Среда геометрического следствия – это среда, где количество, с которым вы должны работать сегодня, является функцией предыдущих результатов. Я думаю, что это особенность мира, в котором мы живем. Оптимальное f – это регулятор роста в такой среде, и побочные продукты оптимального f говорят о скорости роста в этой среде. Из книги вы узнаете, как определять оптимальное f и его побочные продукты для любой формы распределения. Это статистический инструмент, который применим к различным сферам бизнеса и науки. Надеюсь, вы попытаетесь использовать описанные инструменты, чтобы найти оптимальные f не только для рынков, но и для других сфер жизни.

Много лет торговое сообщество обсуждало концепцию управления деньгами. Однако в итоге управление деньгами характеризовалось пестрым набором правил, многие из которых некорректны. Я надеюсь, эта книга даст трейдерам нужную им точность в сфере управления капиталом.

Глава 1 Эмпирические методы

Эта глава является кратким изложением книги «Формулы управления портфелем». Цель главы – довести уровень знаний читателей, которые не знакомы с эмпирическими методами, до уровня знаний тех, кто уже знаком с ними.

Какой долей счета торговать?

Когда вы начинаете торговлю, то должны принять два решения: какую позицию открыть, длинную или короткую, и каким количеством торговать. Решение о количестве всегда зависит от баланса на вашем счете. При счете в 10 000 долл. приобретение 100 контрактов на золото будет слишком рискованным. Если на вашем счету 10 млн долл., разве не очевидно, что приобретение одного контракта на золото почти никак не отразится на счете? Признаем мы это или нет, решение относительно того, каким количеством контрактов в определенный момент времени торговать, зависит от уровня баланса на счете.

Если мы будем использовать определенную долю счета в каждой сделке (другими словами, когда будем торговать количеством, соотносимым с размером нашего счета), то добьемся более быстрого прироста капитала.

Количество зависит не только от баланса на нашем счете, а является также функцией некоторых других переменных: нашего предполагаемого убытка в наихудшем случае в следующей сделке; скорости, с которой мы хотим, чтобы рос наш счет; зависимости от прошлых сделок. Доля счета, которую следует использовать для торговли, будет зависеть от многих переменных, и мы попытаемся собрать все эти переменные, включая уровень баланса счета, чтобы в итоге принять достаточно субъективное решение относительно того, каким числом контрактов или акций торговать.

Из этой главы вы узнаете, как принимать математически верные решения в отношении количества и не основывать свои действия на субъективном и, возможно, ошибочном суждении. Вы увидите, что если использовать неправильное количество, то придется заплатить чрезмерную цену, и эта цена будет расти с течением времени.

Большинство трейдеров не уделяют должного внимания проблеме выбора количества. Они считают, что этот выбор в значительной мере случаен и не имеет значения, какое количество использовать, важно только то, насколько они правы в отношении направления торговли. Более того, возникает ошибочное впечатление, что существует прямая зависимость между тем, сколько контрактов открывать, и тем, сколько можно выиграть или проиграть с течением времени.

Это неверно. Как мы увидим, отношение между потенциальным выигрышем и количеством не выражается прямой линией. Это – кривая. У нее есть пик, и именно на этом пике мы достигнем максимального потенциального выигрыша. Из этой книги вы узнаете, что решение о количестве, используемом в определенной сделке, так же важно, как и решение о длинной или короткой позиции. Мы опровергнем ложное мнение большинства трейдеров и покажем, что уровень счета зависит от правильного выбора количества контрактов не в меньшей степени, чем от правильного направления торговли. Не вы управляете ценами, и не от вас зависит, будет следующая сделка прибыльной или убыточной. Однако количество контрактов, которые вы открываете, зависит только от вас. Поэтому ваши ресурсы будут использованы с большей отдачей, если сконцентрироваться на верном количестве.

При любой сделке вы хотя бы приблизительно предполагаете, каким может быть убыток наихудшего случая. Можно даже не осознавать этого, но, когда вы начинаете торговлю, у вас есть ощущение, пусть даже подсознательное, что может произойти в худшем случае. Восприятие худшего случая вместе с уровнем баланса на вашем счете формируют решение о том, каким количеством контрактов торговать.

Таким образом, мы можем сказать, что существует некий делитель (число между 0 и 1) наибольшего предполагаемого убытка для определения количества контрактов. Например, если при счете в 50 000 долл. вы ожидаете в худшем случае убыток 5000 долл. на контракт и открыто 5 контрактов, то делителем будет 0,5, так как:

50 000 / (5000 / 0,5) = 5.

Другими словами, у вас есть 5 контрактов на счет в 50 000 долл., т. е. 1 контракт на каждые 10 000 долл. баланса. Вы ожидаете в худшем случае потерять 5000 долл. на контракт, таким образом, вашим делителем будет 0,5. Если бы у вас был 1 контракт, то делителем в этом случае было бы число 0,1, так как:

50 000 / (5000 / 0,1) = 1.

Этот делитель мы назовем переменной f. Таким образом, сознательно или подсознательно при любой сделке вы выбираете значение f, когда решаете, сколько контрактов или акций приобрести.

Теперь посмотрите на рис. 1.1. На нем представлена игра, где у вас 50 %-ный шанс выиграть 2 долл. против 50 %-ного шанса потерять 1 долл. в каждой игре. Отметьте, что здесь оптимальное f = 0,25, когда TWR = 10,55 после 40 ставок (20 последовательностей +2, –1). TWR – это относительный конечный капитал (Terminal Wealth Relative), он представляет доход по вашим ставкам в виде множителя. TWR = 10,55 означает, что вы увеличили бы в 10,55 раза ваш первоначальный счет или получили бы 955 % прибыли. Теперь посмотрите, что произойдет, если вы отклонитесь всего лишь на 0,15 от оптимального f = 0,25. Когда f равно 0,1 или 0,4, ваш TWR = 4,66. Это не составляет даже половины того, что будет при 0,25, причем вы отошли только на 0,15 от оптимального значения и сделали только 40 ставок!

О какой сумме мы говорим? При f = 0,1 вы ставите 1 долл. на каждые 10 долл. на счете. При f = 0,4 вы ставите 1 долл. на каждые 2,50 долл. на счете. В обоих случаях получаем TWR = 4,66. При f = 0,25 вы ставите 1 долл. на каждые 4 долл. на счете. Отметьте, что если вы ставите 1 долл. на каждые 4 долл. на счете, то выигрываете в два раза больше после 40 ставок, чем в случае ставки 1 долл. на каждые 2,50 долл. на вашем счете! Очевидно, что не стоит излишне увеличивать ставку. При ставке 1 долл. на каждые 2,50 долл. вы получите тот же результат, что и в случае ставки четверти этой суммы, т. е. 1 долл. на каждые 10 долл. на вашем счете! Отметьте, что в игре 50/50 вы выигрываете вдвое больше, чем проигрываете, а при f = 0,5 вы «остаетесь при своих»! При f > 0,5 вы проигрываете в этой игре, и теперь окончательное разорение – просто вопрос времени! Другими словами, если f (в игре 50/50, +2, –1) на 0,25 отклоняется от оптимального, вы будете банкротом с вероятностью, которая приближается к определенности, если продолжать играть достаточно долго. Таким образом, нашей целью будет объективный поиск пика кривой f для данной торговой системы.

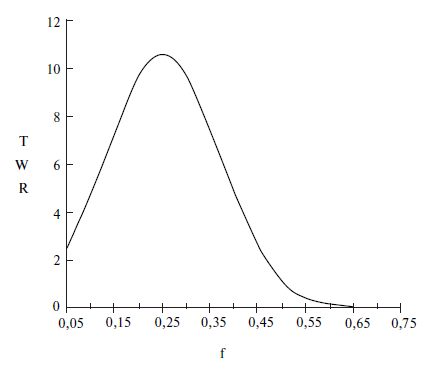
Рис. 1.1. 20 последовательностей +2, –1

В этой книге определенные концепции освещаются с позиции азартных игр. Основное отличие азартной игры от спекуляции заключается в том, что азартная игра создает риск (и отсюда многие настроены против нее), в то время как спекуляция является переходом уже существующего риска (предположительного) от одной стороны к другой. Иллюстрации азартных игр используются для наглядного показа излагаемых концепций. Математика управления капиталом и принципы, используемые в торговле и азартных играх, довольно похожи. Основная разница состоит в том, что в математике азартных игр мы обычно имеем дело с распределением Бернулли (только два возможных исхода), в то время как в торговле сталкиваемся со всем распределением результатов, которые только могут быть в реальной сделке.

Основные концепции

Вероятность задается числом от 0 и 1, которое определяет, насколько вероятен результат, где 0 – это полное отсутствие вероятности происхождения определенного события, а 1 означает, что рассматриваемое событие определенно произойдет. Процесс независимых испытаний (отбор с замещением) – это последовательность результатов, где значение вероятности постоянно от одного события к другому. Бросок монеты является примером такого процесса. Каждый бросок имеет вероятность 50/50 независимо от результата предыдущего броска. Даже если последние 5 раз выпадал орел, вероятность того, что при следующем броске выпадет орел, все равно не изменится и составит 0,5.

Другой тип случайного процесса характеризуется тем, что результат предыдущих событий влияет на значение вероятности, и, таким образом, значение вероятности непостоянно от одного события к другому. Эти виды событий называются процессами зависимых испытаний (отбор без замещения). Игра «21 очко» является примером такого процесса. После того как вытаскивают карту, состав колоды изменяется. Допустим, что новая колода перемешивается и одна карта удалена, скажем бубновый туз. До удаления этой карты вероятность вытянуть туза была 4/52, или 0,07692307692. Теперь, когда туза вытащили из колоды и не вернули обратно, вероятность вытянуть туза при следующем ходе составляет 3/51, или 0,05882352941.

Различие между независимыми и зависимыми испытаниями состоит в том, что вероятность или фиксирована (независимые попытки), или меняется (зависимые попытки) от одного события к другому в зависимости от предыдущих результатов. Фактически это и есть единственное различие.

Серийный тест

Когда в случае с колодой карт мы проводим отбор без замещения, можно путем проверки определить, существует ли зависимость. Для определенных событий (таких как поток прибыли и убытков по сделкам), где зависимость не может быть определена путем проверки, мы будем использовать серийный тест. Серийный тест подскажет нам, имеет ли наша система больше (или меньше) периодов последовательных выигрышей и проигрышей, чем случайное распределение.

Цель серийного теста – найти счет Z для периодов выигрышей и проигрышей в системной торговле. Счет Z означает, на сколько стандартных отклонений вы удалены от среднего значения распределения. Таким образом, счет Z = 2,00 означает, что вы на 2 стандартных отклонения удалились от среднего значения (ожидание случайного распределения периодов выигрышей и проигрышей).

Счет Z – это просто число стандартных отклонений, на которое данные отстоят от среднего значения нормального распределения вероятности. Например, счет Z = 1,00 означает, что данные, которые вы тестируете, отклонены на 1 стандартное отклонение от среднего значения.

Счет Z затем переводится в доверительную границу, которая иногда также называется степенью достоверности. Площадь под кривой нормального распределения вероятности шириной в 1 стандартное отклонение с каждой стороны от среднего значения равна 68 % всей площади под этой кривой. Преобразуем счет Z в доверительную границу. Связь счета Z и доверительной границы следующая: счет Z является числом стандартных отклонений от среднего значения, а доверительная граница – долей площади под кривой, заполненной при таком числе стандартных отклонений.

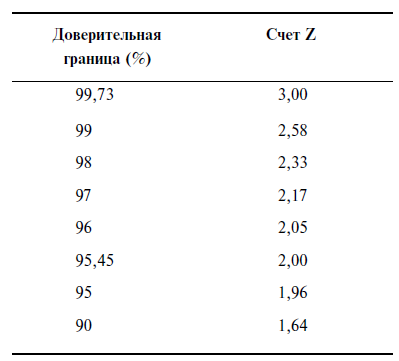
При минимальном количестве 30 закрытых сделок мы можем рассчитать счет Z. Попытаемся узнать, сколько периодов выигрышей (проигрышей) можно ожидать от данной системы? Соответствуют ли периоды выигрыша (проигрыша) тестируемой системы ожидаемым? Если нет, существует ли достаточно высокая доверительная граница, чтобы допустить, что между сделками существует зависимость, т. е. зависит ли результат текущей сделки от результата предыдущих сделок?

Ниже приведено уравнение серийного теста. Счет Z для торговой системы равен:

Z = (N * (R – 0,5) – X) / ((X * (X – N)) / (N – 1)) ^ (1/2), (1.1)

где N – общее число сделок в последовательности;

R – общее число серий выигрышных или проигрышных сделок;

X = 2 * W * L;

W – общее число выигрышных сделок в последовательности;

L – общее число проигрышных сделок в последовательности.

Этот расчет можно провести следующим образом.

1. Возьмите данные по вашим сделкам.

а) Общее число сделок, т. е. N.

б) Общее число выигрышных сделок и общее число проигрышных сделок.

Теперь рассчитайте Х:

Х = 2 * (Общее число выигрышей) * (Общее число проигрышей).

в) Общее число серий в последовательности, т. е. R.

2. Предположим, что произошли следующие сделки:

– 3, +2, +7, –4, +1, –1, +1, +6, –1, 0, –2, +1.

Чистая прибыль составляет +7. Общее число сделок 12, поэтому N = 12. Теперь нас интересует не то, насколько велики выигрыши и проигрыши, а то, сколько было выигрышей и проигрышей, а также серий. Поэтому мы можем перевести наш ряд сделок в простую последовательность плюсов и минусов. Отметьте, что сделка с нулевой прибылью считается проигрышем. Таким образом:

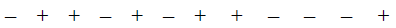
Как видим, последовательность состоит из 6 прибылей и 6 убытков, поэтому Х = 2 * 6 * 6 = 72. В последовательности есть 8 серий, поэтому R = 8. Мы называем серией каждое изменение символа, которое встречается при чтении последовательности слева направо (т. е. хронологически).

1. Последовательность будет выглядеть следующим образом:

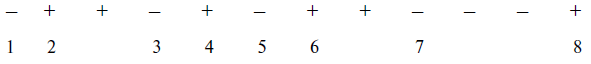
2. Вычислите значение выражения:

N * (R – 0,5) – X.

Для нашего примера:

= 12 * (8–0,5) – 72 = 12 * 7,5 – 72 = 90–72 = 18.

3. Вычислите значение выражения:

(X * (X – N)) / (N – 1).

Для нашего примера:

= (72 * (72–12)) / (12 – 1) = (72 * 60) / 11 = 4320 / 11 = 392,727272.

4. Возьмите квадратный корень числа, полученного в п. 3. В нашем примере:

392,727272 ^ (1/2) = 19,81734777.

5. Разделите ответ из п. 2 на ответ из п. 4. Это и есть счет Z. В нашем примере:

18 / 19,81734777 = 0,9082951063.

6. Теперь преобразуйте счет Z в доверительную границу. Распределение периодов является биномиальным. Однако, когда рассматриваются 30 или больше сделок, мы можем использовать нормальное распределение как близкое к биномиальному. Таким образом, если вы используете 30 или более сделок, вы просто можете преобразовать ваш счет Z в доверительную границу, основываясь на уравнении (3.22) для нормального распределения.

Серийный тест подскажет вам, содержит ли ваша последовательность выигрышей и проигрышей больше или меньше полос (серий выигрышей или проигрышей), чем можно было бы ожидать от действительно случайной последовательности, в которой нет зависимости между испытаниями. Так как в нашем случае мы находимся на уровне относительно низкой доверительной границы, то можно допустить, что между сделками в этой последовательности нет зависимости.

Если счет Z имеет отрицательное значение, то при расчете доверительной границы просто возьмите его абсолютное значение. Отрицательный счет Z говорит о положительной зависимости, т. е. полос меньше, чем при нормальном распределении вероятности, и, следовательно, выигрыши порождают выигрыши, а проигрыши порождают проигрыши. Положительный счет Z говорит об отрицательной зависимости, т. е. полос больше, чем при нормальном распределении вероятности, и, следовательно, выигрыши порождают проигрыши, а проигрыши порождают выигрыши.