
Полная версия
Исследование и оценка параметров сигналов в распределенных информационных системах. Для студентов технических специальностей
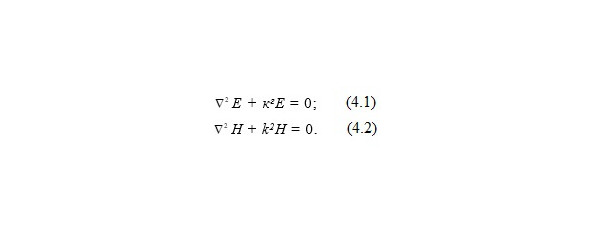
Аналогия ЭМП и гравитационного поля
В математической модели гравитационное поле описывается уравнениями (1.9 и 1.10). Покажем, что это уравнение аналогично уравнению Максвелла для электростатического поля. Так как задача определения потенциала гравитационного поля и силы, действующей со стороны поля на пробную единичную массу, может быть поставлена как задача об определении функции Φ (х,у,z), исчезающей в бесконечности и удовлетворяющей уравнению Лапласа всюду вне V и уравнению Пуассона всюду внутри V, или как задача определения сил F, удовлетворяющих уравнениям (1.8) и (1.10). Такого рода постановка задачи в теории ньютоновского потенциала полностью аналогична постановке задачи электростатики на основе уравнений Максвелла. Можно показать, что решение в бесконечном пространстве задачи об отыскании функции Φ (х,у,z) исчезающей в бесконечности, приводит к формуле (1.7), выражающей собой закон гравитационного тяготения.
Векторной характеристикой гравитационного поля является его напряженность – силовая характеристика точки поля тяготения, равная отношению силы тяготения F, действующей на помещенную в него материальную точку к массе этой точки m.
Предположение о существовании гравитационных волн есть один из вариантов решения уравнений Эйнштейна.
Существование электромагнитных волн также было результатом одного из возможных решений уравнений Максвелла (переменное движение электрических зарядов и переменные электрические токи являются источниками электромагнитных волн).
Точно также считается, что переменное движение массы приводит к излучению гравитационных волн. В настоящее время гравитационные волны определяют как переменное гравитационное поле, распространяющееся со скоростью света и проявляющееся в возникновении относительных ускорений тел.
Интерпритация модели для реальных объектов защиты информации
На рис.2 представлена реальная картина наличия физических полей, их суперпозиция и взаимодействия для простого объекта информатизации, в качестве которого выбрано автоматизированное рабочее место на базе одного персонального компьютера. Разнообразие параметров физических полей представлено напряженностью электрического поля E, напряженностью магнитного H и электромагнитного E,H полей, частотой f, коэффициентом модуляции, спектром сигнала, напряжением, током и другими параметрами.
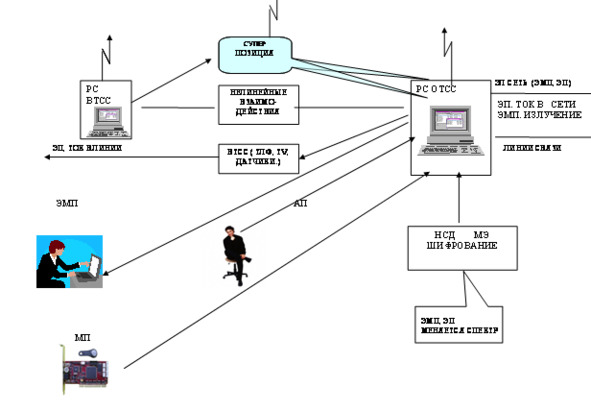
Рис. 2 – Картина физических полей, их суперпозиция и взаимодействия для автоматизированного рабочего места на базе одного персонального компьютера
Рис.3 отражает картину акустического поля, его суперпозицию и нелинейные взаимодействия на примере помещения, где циркулирует защищаемые акустические поля. Поле характеризуется такими параметрами: как: частота f, давление P, колебательная скоростьVk, ускорение а, разборчивость речи W и др.
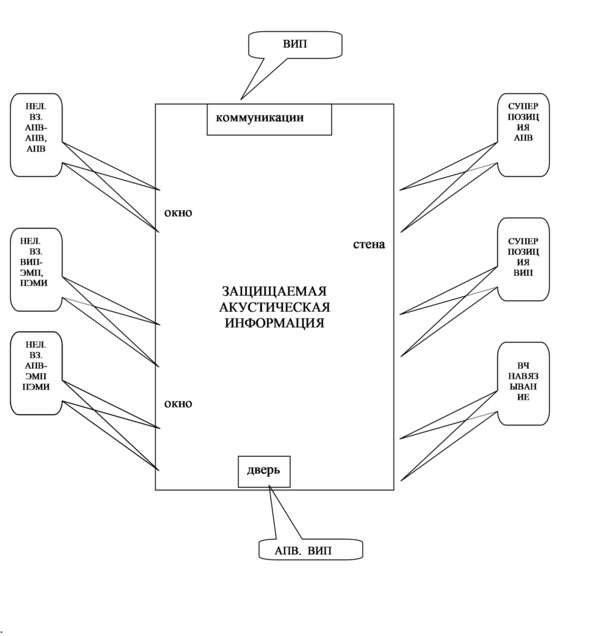
Рис. 3 – Картина акустического поля, его суперпозиция и нелинейные взаимодействия на примере одного помещения
Вывод
1 Введено понятие информации как физическое поле.
2 Показано, что вся информация, сформированная и воспринимаемая – это физическое поле или суперпозиция и взаимодействие полей.
3 Представлена математическая модель физических полей.
4 Показана аналогия описания и изучения физических полей с помощью волновых уравнений.
5 Материал данной работы является исходными данными для реализации модели исследования согласно Рис. 1.
Взаимодействие полей
Исследование взаимодействия физических полей для задач защиты информации
Рассмотрим информацию как многообразия физических полей, их суперпозиции и нелинейных взаимодействий. Взаимодействие составляющих физических полей показаны на рисунке 4.
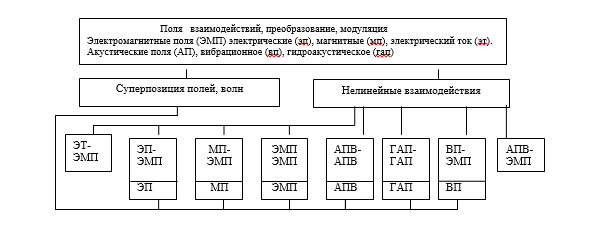
Риc. 4 – Поля взаимодействий
Модель линейных взаимодействий
Отклик или реакция среды на внешнее воздействие физического поля или результат взаимодействия физических полей обозначим буквой О. Воздействия – В.
В отсутствие нелинейных структур, сред, элементов результат взаимодействия описывается линейной зависимостью (5.1),где α – восприимчивость воздействия.
Линейность описывает выполнение принципа суперпозиции (наложения, сложения). Линейные процессы, линейные закономерности и линейные зависимости встречаются часто в физических системах и в процессе взаимодействия.
Линейность предполагает выполнение принципа суперпозиции (наложения, сложения). В этом смысле линейность – категория конструктивная. Зная результат действия каждой из двух (или многих) сил на тело заданной массы и пользуясь принципом суперпозиции, можно ответить на вопрос: «Как будет двигаться это же тело под действием суммарной силы?». Это же можно сказать и о действии суммарного электрического или магнитного полей. Примеры можно продолжить
В природе встречаются линейные процессы, линейные закономерности и линейные зависимости. Как теперь стало понятно, линейные закономерности скорее исключение.
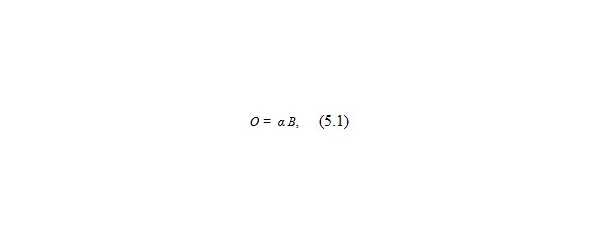
Рассмотрим суперпозицию ЭМП-ЭМП и поляризацию
ЭМП рассматривали как волновой процесс, который описывается однородным уравнением Гельмгольца (6.1), где (6.2) – оператор Лапласа, (6.3) – волновое число или постоянная распространения, (6.4) – абсолютные диэлектрическая и магнитная проницаемости, (6.5) – относительные диэлектрическая и магнитная проницаемости.
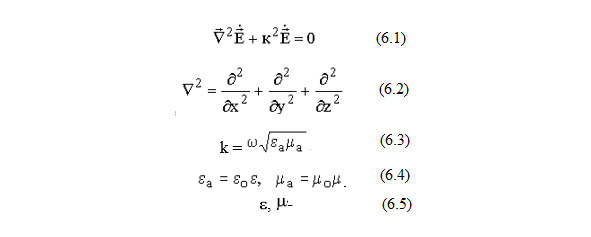
Рассмотрим плоскую электромагнитную волну. Это волновой процесс, у которого амплитуды электрической и магнитной составляющих поля во всех точках плоскости, перпендикулярной направлению распространения волны, имеют одинаковые значения.
Волновое уравнение для плоского поля является линейным дифференциальным уравнением, сумма нескольких его решений также будет являться решением этого уравнения. Таким образом, сложные типы электромагнитных волн можно представлять себе составленными из большого числа элементарных плоских волн с различными амплитудами, фазами и направлениями распространения. В большинстве практических задач, однако, эта точка зрения имеет лишь методическое значение; методы количественного анализа для таких задач будут рассмотрены ниже. Лишь в случае, когда элементарные плоские волны распространяются в одном и том же направлении, имеет смысл вместо суммарной волны рассматривать её элементарные составляющие и находить суммарные свойства путём суперпозиции свойств составляющих. Для таких сложных волн ориентация векторов поля описывается понятием поляризации волны (рис.5).
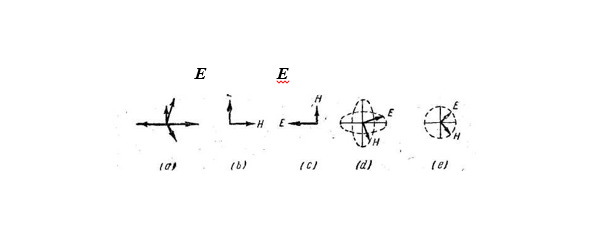
Рис. 5 – (а) Неполяризованная волна, (b) Вертикально поляризованная волна, (с) Горизонтально поляризованная волна, (d) Эллиптически поляризованная волна, (е) Волна, поляризованная по кругу.
Для элементарной плоской однородной волны векторы электрического и магнитного полей всегда взаимно перпендикулярны в любой точке пространства.
Сочетание элементарных волн, распространяющихся в одном направлении, при произвольной ориентации их векторов поля, называется неполяризованной волной. Её отдельные составляющие волны могут иметь также произвольные амплитуды и фазы [рис.].
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.


