
Полная версия
Естествознание
Глава 2. Масштабы реального мира
Сформулируем вначале общую задачу, которую мы надеемся решить, излагая некоторые отдельные положения естественных наук. Хотелось бы, используя знания, накопленные естественными науками в течение нескольких тысячелетий, дать представление о картине мира, какой она видится ученым-естественникам сегодня. Это не философская интерпретация мира, в которой все определяется наиболее общими законами, работающими везде и всюду, и в которой не найдешь деталей. Это набросок того, что уже известно (или кажется известным), и того, что остается под вопросом или требует экспериментального подтверждения, того, что кажется совершенно ясным, и несоответствий, которые возникают при принятии нескольких совершенно ясных понятий одновременно. Это картина гармонии и противоречий. Конечно, вряд ли нам удастся увидеть всю ее целиком, это под силу очень немногим даже из среды ученых. Но изображение отдельных фрагментов, их сочетаний и общий план, возможно, проявится, если чуть-чуть постараться. Главное, чтобы проявилось ощущение интереса, тогда образы внешнего мира станут более доступными и отчетливыми.
Для того чтобы двигаться вперед, нужно знать, какое расстояние необходимо преодолеть. Поэтому начнем с размеров той части мира, которая нам знакома. А дальше будем продолжать движение настолько далеко, насколько нам позволят рамки знания, имеющегося в фундаментальных науках.
В качестве начала отсчета расстояния выберем размер, соответствующий (близкий к) размеру человеческого тела – самый привычный для нас размер. Все люди имеют разный рост (различный размер обуви, разный объем талии, различную ширину плеч). Поэтому в качестве единицы длины просто возьмем 1 м (один метр). Это совсем не значит, что средний рост человека равен 1 м, но метровой длиной (метровая линейка, портновский метр и т. д.) легко измерять любые другие размеры (размеры других объектов) и сравнивать их между собой. Поэтому 1 м мы выбираем как единицу шкалы масштабов для всех расстояний, на которые будем в дальнейшем (мысленно) перемещаться.
Нарисуем прямую горизонтальную линию (рис. 1), середину которой отметим точкой и обозначим ее цифрой 1. Это значит, что точка 1 соответствует размеру (длине) 1 м. Справа и слева, там, где прямая упирается в рамку страницы, поставим стрелки; справа – стрелку вправо, слева – стрелку влево. Таким образом, мы изобразили шкалу масштабов мира; при движении от 1 м вправо размеры увеличиваются, при движении влево – уменьшаются. Постараемся расположить на этой линии все мыслимые размеры, которые описывают строение мира и которые можно сопоставить с какими-нибудь реальными расстояниями – от самых больших до самых мизерных. Будем двигаться вначале вправо, т. е. в сторону увеличения размеров.
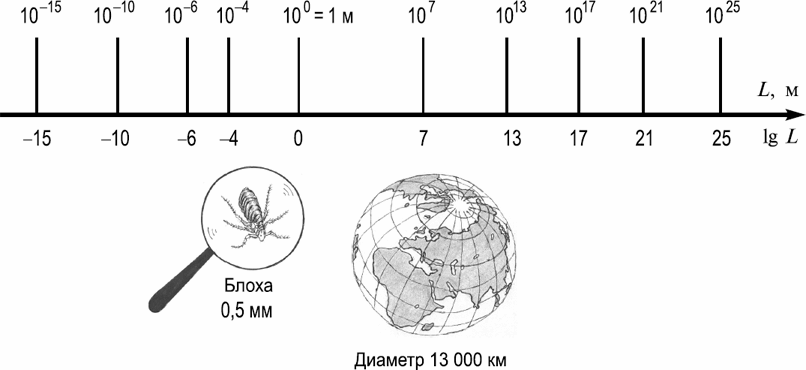
Рис. 1. Шкала масштабов мира
Если точка начала отсчета, первый размер, самый близкий и понятный нам – 1 м, то в качестве первого шага вправо выберем максимальное расстояние, которое человек может пройти по земной поверхности в течение всей своей жизни. Понятно, что физические силы и возможности ходить пешком у каждого человека свои. Так, спортсмены и путешественники за год или чуть больший срок могут пересечь из конца в конец целые страны, такие как США, Канада и даже Россия. Средний городской житель, конечно, на такое не способен. Но оценим, какое он может пройти расстояние в городских условиях, если его пеший путь от дома до работы (школы, института) составляет, скажем, всего 500 м, т. е. 0,5 км. За день его общий путь составит только лишь 1 км. Однако в году 365 дней. Ну, оставим человеку 65 дней на отдых (выходные), во время которых он не обязан выходить из дома (хотя может гулять по паркам, лесам, совершать туристические походы и т. д., но это мы не станем учитывать, намеренно сократив длину его пешего жизненного пути). Тогда путь в течение года составит 300 км. Если считать, что человек регулярно ходит на работу (учебу, в детский сад) в течение 50 лет (это тоже не наибольший срок), то общая длина пути человека за все это время составит не так мало: 300 × 50 = 15 000 км (диаметр Земли составляет около 12 800 км). Уменьшим это расстояние в 1,5 раза (чтобы включить в рассмотрение самых медленных пешеходов и чтобы легче дальше было сравнивать масштабы), т. е. до 10 000 км, и отметим его точкой на масштабной шкале. Для этого вначале переведем расстояние в метры, т. е. умножим на 1000 (в 1 км 1000 м), получим 10 000 000 м (десять млн метров) и представим это число с помощью степени – 107 м. На нашей шкале сопоставим это расстояние числу 7. И дальше будем делать так же, все расстояния будем представлять степенью с основанием 10 и показатель степени отмечать на шкале масштабов, т. е. будем измерять все длины в логарифмическом масштабе. Это позволяет весь мир, какой мы знаем и можем себе представить, уместить на одной странице. Для наглядности у размерной линии, обозначающей данное расстояние, будем ставить два числа: сверху будем писать его в виде степени, а ниже – показатель степени. Например, там, где на линии начало отсчета, под черточкой стоит 0, а выше – 100 (см. рис. 1).
Следующий шаг вправо. Так как на первом шаге мы взяли расстояние, близкое к размеру нашей планеты, то второй шаг можно связать с размером планетной системы, к которой Земля относится, с размером Солнечной системы. Не вдаваясь в детали строения Солнечной системы (об этом речь пойдет ниже), заглянем в справочник и отметим, что поперечник Солнечной системы, по современным астрономическим данным, составляет примерно 10 млрд км, или в краткой записи 1010 км. При переводе в метры получается 1013 м, на масштабной шкале следует поставить число 13.
Следующий шаг – как далеко от нас звезды? Опять же справочная литература подсказывает, что до ближайшей звезды от нас – 4 световых года. Или расстояние, которое свет проходит за 4 года. Сколько это составляет в километрах и в метрах? Скорость света – самая большая из всех известных скоростей и, как считается во всех естественных науках – это предельная скорость, более высоких скоростей быть не может. Почему это так и откуда это следует, отдельный вопрос, мы обсудим его в последующих разделах. Итак, скорость света составляет 300 000 км/с. Чтобы найти расстояние S, равное световому году, надо скорость света с умножить на время t, равное году:
L = ct,только время надо выразить в секундах, так как скорость выражается в км/с. В году 365 суток, каждые сутки содержат 24 часа, в каждом часе 60 минут, а в каждой минуте 60 секунд. Поэтому
t= 365 × 24 × 60 × 60 = 31 536 000 c;это примерно 3 × 107 с, большая точность нам для оценок не нужна. Тогда
S= 300 000 × 3 × 107 = 9 × 1012 км,а до ближайшей звезды в 4 раза больше – около 3,6 × 1013 км. Будем считать, что многие звезды, которые мы можем наблюдать ночью на небе, тоже находятся на близком от нас (по звездным меркам) расстоянии. Но это все же в 2–3 раза дальше, чем самая близкая к нам звезда. Поэтому для оценки можно смело взять расстояние 1014 км, оно будет означать среднее расстояние до всех ближайших к Солнечной системе звезд. Это 1017 м, что мы и отметим на шкале масштабов.
Сдвинемся еще вправо. Размеры каких объектов превышают средние расстояния между ближайшими звездами? На ночном небе простым глазом можно наблюдать очень большое количество звезд. Некоторые очень яркие, некоторые еле видны. Но все звезды, которые мы видим, входят в огромную звездную систему под названием наша галактика. Слово «галактика» происходит от греч. galaktikos, что означает молочный, млечный. В русском языке есть похожее красивое название – Млечный Путь. Так называют светлую туманную полосу, которая в ясные ночи хорошо видна в Северном полушарии. Млечный Путь – это и есть галактика, но не вся, а ее часть, которая видна с Земли. В Млечном Пути содержится огромное количество тесно расположенных звезд, которые настолько малы, что для невооруженного глаза выглядят как расплывчатая слабо светящаяся масса. Малы они, потому что очень далеки. Размер всей галактики, ее поперечник составляет огромное расстояние – около 120 000 световых лет, это примерно 1018 км, или 1021 м. Зафиксируем этот размер на масштабной шкале, поскольку мы решили сейчас рассматривать и сравнивать только размеры. А интересное занятие – рассмотрение строения и свойств этой звездной системы, которая является для нас почти целым миром, – отложим чуть-чуть, чтобы вернуться к этому позже.
Можно ли найти в нашем мире еще что-нибудь большее, чем галактика? Или поставим вопрос по-другому: что есть за пределами галактики и, если есть, как далеко оно продолжается? При наблюдении космических объектов с помощью современных телескопов обнаружено, что в космическом пространстве существуют сотни миллионов (!) других галактик, подобных нашей. Все галактики астрономы объединяют в одну общую систему, которую называют Метагалактикой. Метагалактика содержит все, что удается увидеть с помощью самых совершенных оптических приборов. Ее размеры составляют 10–20 млрд световых лет (1022 км = 1025 м). Проставим этот размер, он будет последним справа на нашей масштабной шкале. Потому что дальше заглянуть нельзя – не хватает остроты зрения современных приборов. А что там дальше? Мы еще вернемся к этому вопросу.
Теперь начнем движение влево в сторону уменьшения размеров. Снова будем сопоставлять размеры с человеческими возможностями. На первом этапе представим себе самый маленький объект, который можно увидеть невооруженным взглядом, – песчинку, маковое зернышко, еле заметное насекомое. Считается, что нормальное человеческое зрение дает возможность рассмотрения любых объектов больше 0,1 мм. В метрах это составит 10~4 м, так как 1 мм = 0,001 м, а объект еще в 10 раз меньше (отрицательный показатель степени показывает, сколько знаков после запятой имеется в данном числе, записанном в виде десятичной дроби). Ставим слева от центральной точки 1 м черточку со значением -4.
Дальше в сторону уменьшения масштабов нельзя двигаться без приборов, которые позволяют получать увеличенные изображения любых изучаемых образцов, – без микроскопов. Оптический микроскоп, т. е. микроскоп, который показывает освещенный специальной лампой объект с помощью системы линз, позволяет надежно изучать детали строения и структуры мелких предметов с размерами до 1 микрометра. Кстати, такие же размеры имеют очень мелкие микроорганизмы, простейшие, бактерии. Микрометр – это миллионная доля метра, т. е. 106 м, соответствующая отметка на масштабной шкале -6.
Электронные микроскопы, в которых увеличение создается электронными линзами, а изображение получается при отражении электронов от поверхности изучаемого объекта, позволяют увидеть отдельные молекулы и, в некоторых случаях, даже атомы твердых тел. Размеры молекул простых соединений и атомов составляют несколько десятых долей нанометра. Нанометр – это миллиардная доля метра, 109 м. Мы же отметим на шкале одну десятую нанометра 1010 м как предельный размер, доступный наблюдению с помощью электронной микроскопии.
Еще меньшие размеры наблюдать непосредственно, используя даже самые мощные устройства, не удается. Можно оценивать эти размеры только посредством косвенных методов, иначе говоря, делая заключения о размерах на основе, например, параметров столкновений отдельных субатомных, входящих в состав атома, частиц. Самый важный объект, играющий огромную роль в различных физических экспериментах и теориях и в современной энергетике, это атомное ядро – центральная часть атома, содержащая почти всю его массу и энергию. Косвенные, но многократно подтвержденные данные свидетельствуют, что размер ядер близок к 1015 м. Элементарные частицы, из которых состоят ядра, – протоны и нейтроны – имеют почти такие же размеры. Поэтому внесем число -15 в нашу масштабную шкалу. Оно может считаться последним слева, так как следующая ступень уменьшения размеров находится в области теоретических прогнозов.
Глава 3. Солнечная система
Для получения представления о естественно-научной картине мира начнем последовательное продвижение по шкале масштабов. Так же как и раньше, отправимся вначале в сторону больших размеров.
Солнечная система – это название каждый из нас, безусловно, слышал много раз. В эпоху космонавтики у каждого человека, даже очень далекого от любой науки, есть некоторое представление о Солнечной системе, ближайших к Земле планетах, особенно Луне, о солнечных и лунных затмениях и других космических эффектах. Большая часть сведений о ближнем космосе поступает из средств массовой информации, фантастической литературы. Приведем краткую фактическую характеристику нашей планетной системы (нашего космического дома) не столь красочную (или приукрашенную), как в этих источниках, но более достоверную и пригодную для описания реальной картины.
Солнечной системой называется планетная система, состоящая из Солнца и вращающихся вокруг него небесных тел (рис. 2).
Кроме Солнца, о котором будет отдельный разговор, в состав Солнечной системы входят планеты со своими спутниками, астероиды, кометы и продукты их распада – метеориты, метеорные тела, межпланетная твердая космическая пыль и разреженные космические газы. Пространство Солнечной системы пронизано потоками частиц и световым излучением Солнца. Также всюду имеются гравитационные поля (поля тяготения) и магнитные поля, особенно вблизи крупных массивных тел.
Солнце является динамическим и геометрическим центром всей Солнечной системы. Его масса примерно в тысячу раз превышает общую массу всех остальных вращающихся вокруг него космических тел. Основу Солнечной системы кроме самого

Рис. 2. Схема Солнечной системы
Солнца составляют девять больших планет: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон. Мы их перечислили в последовательности возрастания их расстояния от Солнца. Следует отметить, что несколько лет тому назад большинство астрономов пришло к выводу, что Плутон нельзя считать планетой, он имеет массу и размеры, которые ближе к массам и размерам спутников планет Солнечной системы. Но мы не будем обсуждать вопросы, как назвать Плутон – планетой, спутником или астероидом. Важно только, что это самое далекое от Солнца большое тело Солнечной системы.
Орбиты планет имеют почти круговую форму (очень слабо вытянутые эллипсы) и лежат все (за исключением орбиты Плутона) приблизительно в одной плоскости, которая называется плоскостью эклиптики. Кроме движения вокруг Солнца, все планеты вращаются вокруг своей оси. Это вращение для всех планет, кроме Венеры, совершается в прямом направлении, т. е. как у Земли – с запада на восток. Венера вращается в противоположную сторону – с востока на запад. Солнце также вращается вокруг своей оси, ось вращения Солнца почти перпендикулярна к плоскости эклиптики, что, возможно, связано с происхождением Солнечной системы. Оси вращения большинства планет направлены под некоторым небольшим углом к направлению перпендикуляра к плоскости эклиптики. Только Уран обладает уникальной для Солнечной системы особенностью, ось его вращения лежит почти в плоскости его орбиты.
Размеры и физические свойства планет позволяют разделить их на две группы – планеты земного типа и планеты-гиганты. В первую группу, кроме Земли, входят Меркурий, Венера и Марс. Вторую группу образуют Юпитер, Сатурн, Уран и Нептун. Плутон не может быть отнесен ни к первой, ни ко второй группе.
Самое большое число спутников, которые обнаружены до настоящего времени, имеет Сатурн – 17 спутников. У Юпитера 16 спутников. Сами эти планеты-гиганты вместе с системами своих спутников напоминают миниатюрную Солнечную систему. Уран имеет 15 спутников, по два спутника у Марса и Нептуна. По одному спутнику имеют Земля (как вы понимаете, спутником Земли является Луна) и Плутон. Венера и Меркурий, по астрономическим данным на сегодняшний день, совсем не имеют спутников.
Орбиты практически всех планетных спутников, так же как орбиты планет вокруг Солнца, мало отличаются от окружностей. Если у планеты имеется несколько спутников, то плоскости их орбит в основном совпадают. Большинство спутников обращается вокруг своей планеты в плоскости ее экватора и в прямом направлении (по часовой стрелке), т. е. с запада на восток. По массе и размерам спутники планет также разбивают на две основные группы: крупные планетоподобные спутники с поперечником (диаметром) больше 3000 км (напоминаем, поперечник или, что то же самое, диаметр Земли составляет 12 750 км). В эту группу, кроме Луны, входят четыре самых крупных спутника Юпитера – Ио, Европа, Каллисто, Ганимед, спутник Сатурна Титан и спутник Нептуна Тритон. Вторая группа – это все остальные спутники: от достаточно большого спутника Сатурна Рея (поперечник 1850 км) до самых маленьких спутников планет в Солнечной системе, спутников Марса – Фобос и Деймос, которые представляют собой каменные глыбы несферической формы с размерами 22 × 12 км для Фобоса и 12 × 8 км для Деймоса.
Для того чтобы понять, почему планеты вращаются вокруг Солнца, какие законы управляют их движением, необходимо небольшое дополнительное путешествие…
3.1. Дополнительная информация. Физика
Кинематика изучает движение. В кинематике мы имеем дело с положением тела или частицы, скоростью и ускорением, но не интересуемся ни природой движущихся тел или частиц, ни силами, вызывающими ускорение.
При движении с постоянной скоростью v
s=vt,где s – расстояние, пройденное за время t; отсюда значение скорости определяется как
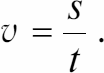
Теперь рассмотрим движение тела со скоростью, которая меняется по величине, но не по направлению (это поступательное движение). Тогда на небольших участках As, которые тело проходит за время At, значения мгновенной скорости определяются как
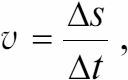
или более строго:
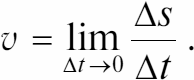
Это соотношение означает, что мгновенная скорость v есть предел отношения As/At при At, стремящемся к нулю (строгое математическое определение значения мгновенной скорости).
Если тело движется на отрезке пути s1 в течение времени t1 с одной скоростью, а на отрезке пути s2 в течение времени t2 с другой скоростью, то средняя скорость v на всем пути:
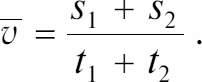
Постоянное ускорение определяется как
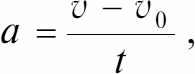
где v – v0 – приращение скорости за время t.
Мгновенное ускорение:
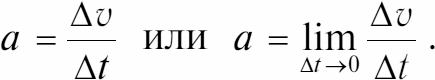
Путь при равноускоренном движении:
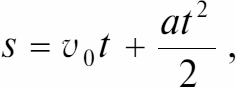
где v0 – скорость тела в начальный момент времени.
На практике нужно знать не только значение, но и направление скорости в пространстве, например, чтобы описать движение (траекторию) автомобиля, самолета или космического корабля. Любая физическая величина, которая не будет полностью определена, если задать только ее значение и не указать, в какую сторону она направлена, является вектором.
Скорость – это вектор. Если разложить вектор скорости v при движении тела в пространстве по осям декартовой системы координат, то мы получим ее составляющие vx, v, vz. Они связаны с полной скоростью v соотношением
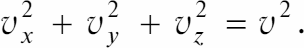
Следует отметить, что векторную природу имеет ускорение a, а также многие величины, которые мы будем использовать в дальнейшем изложении: сила F, импульс p и другие. Во всех случаях векторные величины отмечаются стрелкой «->», помещенной над буквенным обозначением величины. Значение самой величины (ее абсолютная величина) обозначается просто буквой, например, a – значение ускорения.
Рассмотрим равномерное движение тела по окружности со скоростью v. При этом его ускорение, оставаясь перпендикулярным скорости в любой момент времени, направлено к центру окружности. Можно показать, что значение ускорения тела ac, которое в данном случае называется центростремительным, определяется по формуле
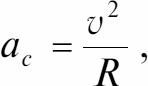
где R – радиус окружности. Следует отметить, что центростремительное ускорение меняет только направление вектора скорости, не влияя на его величину; ускорение ac направлено по радиусу окружности к ее центру.
Пример. Определение первой космической скорости.
Любое тело, движущееся по круговой орбите вокруг Земли, должно иметь ускорение ac = v2/R, направленное к центру нашей планеты.
Поскольку на тело в этом случае действует только сила земного притяжения (т. е. сила тяжести), то можно записать
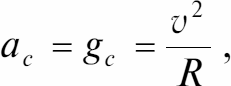
где gc – ускорение свободного падения – 9,8 м/с2.
Тогда vc = qR.
Если считать, что R≈ 6500 км (расстояние до центра Земли), то вычисление первой космической скорости дает значение vc=8 км/c. Если разделить длину орбиты на скорость спутника, то получим время одного оборота спутника вокруг Земли. Длина орбиты низколетящего спутника близка к длине экватора Земли t = 40 000 км/8 км/c = 5000 c = 83 мин
Для того чтобы вывести ракету за пределы действия земного притяжения, т. е. направить ее к другим планетам, необходимо сообщить ей начальную скорость 11,2 км/с, которая носит название второй космической скорости.
Впервые эти расчеты провел Исаак Ньютон еще примерно в 1660 г.
Динамика занимается изучением общих законов взаимодействия материальных тел. Широкий класс явлений удается описать или объяснить на основе законов движения И. Ньютона.
Первый закон Ньютона
Будучи предоставлено самому себе (при отсутствии результирующей внешней силы), тело сохраняет состояние покоя или равномерного движения с равным нулю ускорением.
В математической форме это утверждение имеет вид: a = 0, если F = 0 (F – результирующая внешняя сила).
Второй закон Ньютона
Действующая на тело результирующая сила равна произведению массы тела на его ускорение:
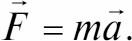
Третий закон Ньютона
При любом взаимодействии двух тел сила, с которой первое тело воздействует на второе, равна по величине и направлена противоположно силе, с которой второе тело воздействует на первое:
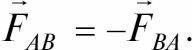
Все три закона движения справедливы только при условии, что наблюдатель находится в инерциальной системе отсчета. Определение Ньютона для инерциальной системы отсчета: это любая система, которая покоится или движется равномерно и прямолинейно по отношению к неподвижным звездам.
Определение: импульсом (количеством движения) тела p называется произведение массы тела на его скорость:
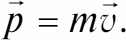
Закон сохранения импульса
В отсутствие внешних сил сумма импульсов системы частиц (тел) остается неизменной.
При столкновении двух частиц, имеющих массы mA и mB, закон сохранения импульса записывается так:
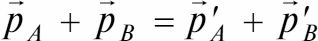
или










