Научная журналистика как составная часть знаний и умений любого ученого. Учебник по научно-популярной журналистике

Увертюра к главе 3

Образование – замечательная вещь, но время от времени полезно вспоминать, что ничему действительно стоящему научить невозможно.

Оскар Уайльд

«День и ночь». Мауриц Эшер

Сейчас я хочу кратко просуммировать все вышесказанное, при этом взглянув на него под новым углом зрения, который стал нам теперь доступен. Думается, это не будет пустой тратой времени. Казалось бы, мы можем без остановок и проволочек двигаться дальше. И это было бы так, если бы не одно обстоятельство.

Поскольку без возражений был принят тезис о том, что научный журналист не только может, но просто обязан использовать достижения науки в своей профессиональной деятельности, то вы, очевидно, догадались, что в какой-то мере достижения эти уже были использованы научным журналистом, и вы стали тому свидетелями, если угодно – жертвами, хотя лучше сказать – соучастниками. Теперь, повторяя в тезисном, телеграфном стиле то, что было сказано, я собираюсь при этом частично раскрыть карты – объяснить, почему это было сделано так, а не иначе, и какую конечную цель преследовал тот или иной пассаж.

Итак, о чем и как мы говорили?

Сначала были использованы пассы массового гипноза. Разными способами внушалась мысль, что профессия научного журналиста – одна из самых привлекательных, нужных и перспективных, не говоря уж о том, что она расширяет кругозор, вводит в контакт с действительно умными и интересными людьми, дает пищу уму и сердцу. Использовались ностальгические, воздействующие на эмоциональную сферу читателя, воспоминания о былых миллионных тиражах научно-популярных изданий, могучих отделах науки во всех уважающих себя газетах и толстых журналах. Эта часть исполнялась на клавикордах, в лирическом ключе, расслабляя сознание читателя и готовя его к восприятию следующей, на этот раз бравурной мелодии.

Ее вела звучная медь тромбонов оптимизма. Они возвещали благую весть о том, что маятник общественного интереса к науке прошел нижнюю точку – момент безразличия, почти презрения к ней – и неуклонно движется к прежнему почитанию и желанию быть в курсе последних научных веяний и достижений. Вновь приводились различного вида аргументы в пользу этого положения и чисто бытовые, и общефилософского характера, вроде того, что каждое новое открытие в науке лишь расширяет сферу непознанного и тем создает новые рабочие места для научных журналистов. Задачей этой суггестии было внедрить в сознание читателя мысли, что становиться научным журналистом сегодня – дело во всех смыслах стоящее, даже выгодное.

Затем был проведен сеанс психотерапии. Целью его было снять страх перед общением с учеными, побороть комплекс неполноценности, вызванный реальным или кажущимся недостатком знаний о науке у будущих научных журналистов. Обсуждались две схожие между собой модели ученого как части общества, каждая из которых приводила к выводу, что ученый в неменьшей степени заинтересован в помощи журналиста, профессионально пишущего о науке, в его таланте и умении, чем этот журналист заинтересован в информации о сделанном ученым в науке. В нужный момент вступили литавры – прозвучало малоизвестное высказывание Альберта Эйнштейна о решающей роли научно-популярной литературы в прогрессе человечества. Начиная с этого момента никто уже не страшился контактов с учеными и научными проблемами, и на извечный вопрос российской интеллигенции «что делать?» все хором отвечали: «идти – нет, бежать, нестись, мчаться – в научную журналистику».

Тут, следуя Штирлицу, знавшему об открытом психологами и физиологами свойстве памяти фиксировать последнее событие или сообщение, было сказано о еще одной, быть может, наиглавнейшей причине, почему научный журналист – одна из главных фигур прогресса. Ученому, как время от времени и всякому человеку вообще, необходимо оторваться от своих сиюминутных забот и взглянуть на свою жизнь и работу сверху, в более широкой перспективе, увидеть ее связь с другими исследованиями, сопоставить с результатами, полученными в других науках. «И здесь, – вкрадчиво пропела скрипка, – ученому не обойтись без хорошо и всесторонне информированного и умеющего эту информацию изложить на понятном другим языке научного журналиста».

Теперь надо было перейти от общего к частному, подтвердить свои рассуждения примерами, в достоверности которых читатели могли бы легко убедиться. Этого требовала теория восприятия и основы дидактики. Поэтому была предъявлена история вполне реального лица, которое, проработав несколько лет в науке и пристрастившись к писанию научно-популярных вещей, постепенно вырастило в своем сознании и своей душе научного журналиста, вытесняя при этом ученого. Казалось, ученый окончательно умер. Но выяснилось, что он лишь впал в летаргический сон и, проснувшись, родил идею (это стало поворотным моментом), что нелепо изучать все и всяческие науки и взаимодействия между ними и не использовать эти знания в своей профессиональной работе. Иными словами, надо поставить профессию научного журналиста на научную основу.

Тут мы перевели дыхание, а самые проницательные догадались, что принцип этот уже определял все сказанное и продемонстрированное, включая некоторые схемы и зрительные эпиграфы – гравюры Маурица Эшера, памятуя установленный наукой факт, что зрительное восприятие и зрительная память у большинства людей сильнее слуховой, то есть одна картинка стоит тысячи слов.

Затем я прибегнул к доказавшему свою высокую эффективность методическому приему, обычно используемому протестантским пастором, который перед каждой проповедью заранее объявляет своей пастве, о чем он будет говорить, затем сообщает, что писали по данному поводу авторитеты церкви, и в конце – что думает он сам.

Сделать нашу профессию научной – значит найти те приемы и алгоритмы, что позволяют оптимальным образом трансформировать знания, полученные в одной области науки, в иные ее области, даже очень далекие друг от друга, или, рассматривая проблему в более общей перспективе, которые позволяют сделать эти знания достоянием самой широкой аудитории. Эти приемы и алгоритмы реально существуют в природе, научный журналист заимствует их у науки и использует для ее популяризации.

В то же время абсурдно считать, будто в нашей власти управлять человеческим сознательным (а в еще меньшей степени – бессознательным) поведением, чтобы наладить перенос такого деликатного продукта, как знание, из одной головы в другие. (Автор эпиграфа к этой Увертюре, Оскар Уайльд, известен парадоксальностью своих высказываний, но тут он, видимо, сказал впрямую то, что думал.) Инструкций, как делать это, действуя шаг за шагом, вы не найдете нигде – их попросту нет в природе. То есть научная популяризация, даже используя методы и приемы науки, очень сильно от нее отличается. Познавать законы мира и делать результаты таких исследований доступными людям – две очень разные вещи. Сие означает, что научная популяризация, как и всякое искусство вообще, принципиально не алгоритмизуема. Но! Ядром всего последующего разговора явятся поиски этих несуществующих в природе алгоритмов.

Поэтому было положено на музыку математических формул высказывание Эйнштейна, которое приведено в предыдущей главе: Эйнштейн выразил свою мысль столь афористично, столь ясно, что слова его дали толчок (или послужили намеком) для создания гипотезы – осмелюсь сказать, первой научной гипотезы в науке о научной популяризации. А именно, что самый фундаментальный закон Природы – закон сохранения, например, сохранения энергии или массы, каковые никогда не исчезают, а как говаривал Михайло Ломоносов, «если в одном месте что убудет, то в другом присовокупится», – этот всеобщий закон сохранения верен и для такой сложной области как научная журналистика.

Стоит лишь облечь слова великого физика в математическую форму, и мы сразу получаем уравнение

I = C/A

или, что то же самое,

I × A = C = const,

где I – Понятность, A – Точность, C – некая постоянная величина.

В словесном выражении гипотеза звучит так:

Понятность изложения обратно пропорциональна ее Точности, или, что то же самое, произведение Точности изложения на его Понятность есть величина постоянная. То есть чтобы добиться большей Понятности, неизбежно приходится жертвовать Точностью, и наоборот.

И отсюда вывод: следует стремиться к максимальному значению постоянной С в данных гиперболических зависимостях.

И вот мы оказались в положении, когда известно, что делать, но неясно – как. Однако можно сказать, что главная задача все-таки решена, ибо знать направление, в котором следует двигаться, – это больше, чем полдела.

С этого момента мы, оставив позади повторение пройденного и осмысление его с позиций этого самого пройденного, начинаем двигаться дальше. Но прежде взгляните на гравюру Эшера, служащую зрительным эпиграфом к этой Увертюре и попробуйте дать ей свое толкование, то есть объяснение, почему она предваряет всё сказанное в этой главе.

Глава 3

Гипотеза гиперболы, ее смысл и следующие из нее выводы

Нарочитая бессмысленность стала считаться в определенных кругах признаком истинной науки.

Олдос Хаксли

«Небо и вода I». Мауриц Эшер

Мы начнем с иллюстрации, вынесенной в эпиграф.

Гравюра Эшера в зрительной, графической, а потому лучше всего воспринимаемой нашим сознанием форме, показывает, что нам следует выбирать между наиболее полным изображением либо рыбы, либо птицы. Или это рыба научной точности, скрытая в океанических глубинах специальной терминологии, уравнений, формул, графиков, таблиц, сложнейших теорий и гипотез, или же это парящая в чистом воздухе интуиции и эмоций птица ясного, прозрачного и порой даже поэтического, но всегда не совсем точного описания ситуации. Как это вообще очень часто случается в жизни, нельзя получить все и сразу, требуется найти некий компромисс. И наилучшее решение лежит где-то в середине гравюры. Мозаика, составленная из птиц и рыб, позволяет нам видеть обитателей обеих стихий – неба и воды – вполне отчетливо, хотя и не так хорошо, как соответственно вверху и внизу гравюры. В принятых нами терминах это и есть оптимальный способ удовлетворить одновременно требования Точности и Понятности.

Здесь содержится мой первый ответ на вопрос, который вы, без сомнения, давно хотите мне задать: как увеличить величину коэффициента С? Используйте дополнительные средства из арсенала научного журналиста – например, найдите подходящий к случаю зрительный образ.

Бросим еще один взгляд на рис. 3. Гипотеза гиперболы, которую мы обсуждаем, утверждает, что Точность, помноженная на Понятность, есть C, величина постоянная. Чтобы придать нашему анализу истинно научное звучание, станем выражать Точность в экзектонах (от англ. exact, exactness), Понятность – в андерстонах (от англ. understanding). Тогда постоянная

С = AI = [exacton]·[underston] = [gifton].

(Название единицы измерения коэффициента С «гифтон» происходит от англ. gift – дар, талант.)

Таким образом, мера одаренности научного журналиста, 1 гифтон, равен произведению 1 экзетона на 1 андерстон.

Теперь уже даже самый строгий критик не посмеет утверждать, что наша гипотеза лишена научного содержания, а вы с пониманием отнесетесь к этому небольшому розыгрышу.

Вернемся к рис. 3. Из него каждый может легко заключить, что нам следует придерживаться верхней кривой, где С = 64, а не 4. Действительно, пусть Точность А = 8. Тогда на верхней кривой Понятность достигает значения 4, в то время как на нижней оно всего лишь 1/2, что ровно в 8 раз меньше.

Есть несколько путей к этой цели. Но в любом случае добиться успеха можно, лишь умело используя все пять чувств, данных вам Природой, все четыре ведущих колеса вашего воображения, все три измерения пространства, вас окружающего, и обе половины вашего мозга, каждая из которых воспринимает и отражает мир по-своему, чтобы получить один результат – быть понятым другими людьми. В конечном итоге это и есть заветная цель любого разумного существа. Но для научного журналиста это еще и профессиональная обязанность.

У меня больше не припасено методических шуток и розыгрышей, зато я хочу предложить вам цирковой трюк, имеющий прямое отношение к нашему разговору.

Уважаемой аудитории предлагается убедиться, что бывают поверхности, у которых только одна сторона – например лента Мёбиуса. Фокусник на арене держит в руках длинную ленту, затем поворачивает ее вдоль оси на 180° и склеивает концы. К изумлению зрителей оказывается, что теперь ленту можно покрасить только в один цвет.

Можно ли было более наглядно, в еще более понятной и запоминающейся форме рассказать о геометрической идее односторонних поверхностей?

Положительный ответ, при всей его очевидности, неверен.

Остался еще неисчерпаемый ресурс художественного отражения действительности. Перед вами гравюра Эшера, так и названная художником «Лента Мёбиуса». Проследите мысленно путь любого из муравьев, и вы особенно четко представите себе – зрительно, ощутимо, – что такое односторонняя поверхность.

Как вам кажется: есть ли еще пути к дальнейшему повышению коэффициента С, характеризующего профессионализм и талант научного журналиста? Видимо, это конец пути – разве что если бы муравьи на гравюре ожили и мы смогли бы увидеть одностороннюю поверхность, так сказать, в действии.

Этот следующий шаг к вершинам научной популяризации сделан на компьютерном диске «Escher Interactive», в высшей степени интересном, где гравюра эта анимирована. Пытливый читатель сумеет найти нечто подобное и во Всемирной сети.

Еще один путь сделать жизнь научного журналиста легче – добавить к тексту тактильные ощущения и запахи. Единственный пример, известный мне, это представление «Познакомьтесь с Голландией», которое дается несколько раз в день в Амстердаме в помещении, граничащем с музеем Рембрандта. Кресла с вибраторами позволяют вам ощутить воображаемую посадку самолета, мощные вентиляторы, нагнетающие воздух прямо в лицо зрителям, дают испытать чувства человека, мчащегося на моторной лодке, а некоторые специальные добавки в этот воздух напоминают о море, которое вы в этот миг видите на панорамном экране.

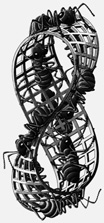
«Лента Мёбиуса». Мауриц Эшер

И в заключение – совсем уж экзотичный пример того, как современная наука приходит на помощь научному журналисту, расширяя диапазон его творческих возможностей. Один из самых запоминающихся аттракционов в парижском Диснейленде – это воображаемый «Институт открытий», где лазерная машинерия позволяет «профессору Зеленскому» запускать в зал виртуальные объекты вроде гигантского питона, который самым правдоподобным образом проглатывает тебя, где бы ты ни сидел в зале, устремляясь со сцены прямо к твоей голове и разевая по дороге свою огромную пасть.

Глава 4

Наука, квазинаука, антинаука и их популяризация

Редактор – человек, который отделяет зерна от плевел, чтобы затем публиковать плевела.

Эдлай Стивенсон

«Порядок и хаос». Мауриц Эшер

Гипербола, отражающая связь между Точностью и Понятностью изложения любого достаточно сложного положения и знакомая нам по рис. 2 и 3, фигурирует и на рис. 4.

Обе ветви гиперболы стремятся в бесконечности коснуться своих осей, но им это никогда не удастся. Математик сказал бы, что гиперболическая кривая асимптотически стремится к значениям Аmin и Imin. Эти две прямые, асимптоты, можно назвать «последней надеждой» как для ученых, так и для научных журналистов. И в самом деле, даже если научный текст состоит из одних лишь формул и специальных терминов, как это обычно и бывает в чисто математических работах, все-таки в нем всегда содержится несколько общепонятных слов вроде «отсюда следует, что», «таким образом теорема доказана», «и наоборот» и тому подобные выражения. То есть всегда существует некая минимальная Понятность, соответствующая на рис. 4 Imin. И наоборот, сколь бы поэтичным и далеким от строгого описания научного положения ни был текст, скажем, в книге для детей дошкольного возраста, в нем всегда содержится некий минимум Точности, на рис. 4 обозначенный как Amin.

Точка Х на кривой с координатами Aperm, Iperm напоминает о том главном выводе, к которому мы пришли ранее: научный журналист должен работать вблизи нее, где и Точность, и Понятность находятся в пределах неких разрешенных (по-английски permissible) границ.

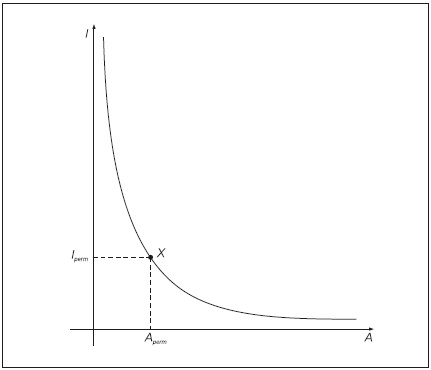
Рис. 4.

До сих пор мы полагали, что и Точность, и Понятность – величины всегда положительные, то есть A > 0 и I > 0. С математической точки зрения это ничем не оправданное допущение, и поэтому теперь мы рассмотрим ситуации, когда либо Точность, либо Понятность, либо обе эти величины отрицательны.

На рис. 5 вы видите все четыре квадранта функции I = C/A и, таким образом, все, что мы рассматривали до сих пор, это квадрант I, представляющий собой лишь частный случай. Сначала мы проанализируем квадранты II, III и IV, а затем вернемся к квадранту I.

Квадрант II. Здесь Точность отрицательна, то есть A < 0, а Понятность положительна, то есть I > 0. Это означает, что текст ясен и понятен, но он неточен или неверен с точки зрения науки. Так бывает либо при вульгаризации науки, когда автор сам не понимает того научного материала, о котором пишет, либо же при популяризации квазинауки, когда идеи переданы верно, но сами они не выдерживают научной критики. Примеров вульгаризации науки сколько угодно в газетных и журнальных статьях, на радио и телевидении.

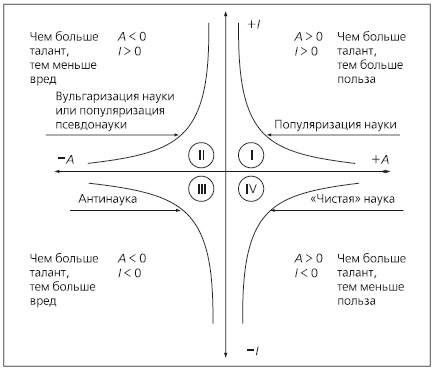
Рис. 5.

Популяризация псевдо- или квазинауки сегодня тоже вещь нередкая – всевозможные астрологические и иные прогнозы, телевизионный сериал «Секретные материалы», который заставил многих доверчивых телезрителей думать, будто все в нем рассказанное – правда.

Квадрант III. Здесь и Точность, и Понятность отрицательны, то есть меньше нуля и A, и I. Это область антинауки в ее наиболее рафинированной и догматической форме.

Я могу привести вам яркий и убедительный пример такой ситуации, с которым вы знакомы, по счастью, лишь по литературе. В советское время долгие годы в обязательном порядке всеми средствами массовой информации популяризировалось учение Трофима Денисовича Лысенко. Он был членом академий, лауреатом всех мыслимых премий, Героем Социалистического Труда, кавалером шести орденов Ленина и т. п. Он утверждал, что генов не существует и что наследственные признаки образуются в течение жизни организма, а потом передаются потомкам. Таким образом, их можно добавлять или исключать простым воздействием окружающих условий. Несколько упрощая его концепцию, образно ее можно представить так: если заставить человека привыкнуть к холодному климату, то и его дети тоже станут холодоустойчивыми. Такой подход очень импонировал Сталину, поскольку работал на его сверхидею – создать советского человека, помещая людей в искусственно созданные сложные социальные и бытовые условия.

Чрезвычайно смешно читать эту страницу истории отечественной науки именно теперь, когда геном человека практически расшифрован, когда споры идут не о возможностях генной инженерии, а о допустимости их с этической точки зрения. Но вот что не смешно и что важно для нас – тот факт, что лысенковские теории постоянно публиковались во всех центральных газетах в полном объеме, хотя никто из читателей не мог понять даже отдельных абзацев – так чудовищно туманно, наукообразно, темно и непонятно теория эта излагалась. У нас будет случай порассуждать, с какой целью это делалось, а сейчас лишь зафиксируем в своей памяти, что отрицательные значения Точности и Понятности ведут к лженауке или к антинауке.

На этом мы временно прощаемся с третьим квадрантом и переходим к четвертому.

Квадрант IV. Это наиболее распространенный случай для так называемой настоящей, или «чистой», науки. Ученые, естественно, заботятся о точности в своих научных публикациях, поэтому в них А всегда положительная величина. Но в большинстве случаев они абсолютно безразличны к тому, будет ли их труд понятен кому-либо, кроме ближайших коллег, не говоря уж о человеке с улицы. Поэтому Понятность таких публикаций становится величиной отрицательной. Это как в средние века, когда вся наука излагалась только на латыни, простым людям непонятной. Или в наше время вся служба в православных храмах идет на церковно-славянском языке, тоже малопонятном верующим.

Бывают, правда, случаи, когда намеренно усложненное изложение, нарочитое злоупотребление специальной терминологией и прочее наукообразие служит во благо. Скажем, декан психологического факультета МГУ Алексей Николаевич Леонтьев, чье столетие отмечалось в 2003 году, именно таким путем умудрился создать своего рода заповедник в советской психологии, где многие выдающиеся ученые могли относительно свободно работать, не страшась нападок со стороны партийного руководства – цензура и чиновники, ответственные за идеологическую чистоту, попросту не могли вникнуть в суть работы этих психологов и просмотрели, что она базировалась на трудах запрещенного в те годы Льва Семеновича Выготского, учителя Леонтьева.

Бросим прощальный взгляд на рис. 5.

В той его четверти, что относится к популяризации науки в наиболее близком нам первом квадранте, как мы установили, чем больше значение постоянной С, тем большая Понятность может быть достигнута при той же Точности, и наоборот, при той же Точности становится доступной большая Понятность. Коэффициент С – это коэффициент профессионализма, мера таланта и умения научного журналиста. Поэтому можно сказать, что в первом квадранте, для нас наиважнейшем, действует принцип: «Чем больше талант, тем больше польза». Имеется в виду, разумеется, польза для общества в целом.

Второй квадрант дает нам другую формулу: «Чем больше талант, тем меньше вред». Естественно, никакой пользы для общества не может быть, когда Точность изложения отрицательна, но талантливый научный журналист может минимизировать те потери, что понесет по его вине читающая публика.

Третий квадрант – худший из всех возможных. Здесь способности автора сыграют против людей, читающих его произведение по своей воле или по принуждению. По счастью, лженаука очень редко влечет к себе гениев пера. Лозунг этой четверти рис. 5, следовательно, таков: «Чем больше талант, тем больше вред».

Ситуация, описываемая последним, четвертым квадрантом, подчиняется правилу: «Чем больше талант, тем меньше польза». Человек, направляющий все свои усилия на то, чтобы результаты научной работы стали доступны лишь ограниченному кругу исследователей только данной области, только элитарному клубу узких специалистов, сводит к минимуму ту пользу, что работа могла бы принести обществу.

Глава 5

Ответственность научного журналиста

И от всякого, кому дано много, много и потребуется, и кому много вверено, с того больше взыщут.

Евангелие от Луки

«Водопад». Мауриц Эшер

Поговорим об ответственности, которую налагает на научного журналиста его профессия. Смысл словесного эпиграфа к этому серьезному и важному разговору, взятого из Нового Завета, ясен. Вообще Библия – литературный источник, знаменитый как точностью, так и понятностью своих текстов. Если бы нам поручили оценить величину коэффициента С, то есть меру профессионализма и талантливости ее авторов, то мы не ошиблись бы, назвав ее очень большой. Что же касается зрительных эпиграфов, традиционно заимствованных у Маурица Эшера, то по заведенному порядку смысл их станет понятным чуть позже.

Чтобы предельно кратко суммировать все сказанное ранее, достаточно взглянуть на рис. 6. Мы выяснили, что существует «область света», где все произнесенное или написанное прозрачно-ясно и доступно пониманию любого разумного человека, и «область тьмы», в которой смысл скрыт от «человека с улицы», то есть от обычного читателя, слушателя или зрителя. Первая расположена выше оси Точности, вторая – ниже нее. В наших силах также отделить «область добра» от «области зла» по тому, верны или, напротив, ложны с научной точки зрения содержащиеся в них высказывания. Добро, то есть дело правое, как ему и положено, располагается справа от оси Понятности. Зло же, отгороженное этой осью, владеет таким же точно по величине полупространством, где Точность отрицательна.