
Полная версия
Космос – Великий Обманщик

Космос – Великий Обманщик
Александр Яковлевич Хорев
Дизайнер обложки Дмитрий Радикович Файзуллин
© Александр Яковлевич Хорев, 2018
© Дмитрий Радикович Файзуллин, дизайн обложки, 2018
ISBN 978-5-4490-5850-8
Создано в интеллектуальной издательской системе Ridero
Предисловие
Когда я был маленьким, я думал, что Земля плоская. Все было просто и понятно. Под ногами была твердая земля, над головой – голубой купол неба. Была комната с прямыми линиями и углами, в один из которых меня иногда ставили за излишнюю любознательность. По утрам на востоке вставало солнце и, совершив свой ежедневный путь, садилось на западе. В то время я еще не обращал внимания на то, что солнце двигалось не по прямой линии. Но меня уже немного смущало то, что линия горизонта представляла собой круг. Было бы привычней, если бы это был прямоугольник, как бабушкино картофельное поле. Я тогда и представить себе не мог, что где-то может существовать иной непривычный мир, в котором нет ни одной прямой линии. Я думал, это возможно только в смешном детском стихотворении про человечка со скрюченными ножкам, который гулял по скрюченной дорожке. Чтобы не нарушать ни чьих авторских прав, я решил дать свой вариант трактовки непрямых линий:
За извилистою речкой, НедалечеЖил ужасно косолапый человечек.Он по круглой планете ЗемляНе ходил, а писал кренделя.Он бы так и писателем стал,Но вот дергал же черт его.Он одною ногой писал,А другою все время зачеркивал.И хотя он в трех соснах плутал,Никогда он не унывал,Потому что твердил его дед,Что кривая куда-нибудь выведет.Потом, когда мне стали попадаться в руки книги, я запомнил две картинки. На одной была изображена Земля в виде чаши, которую держали три слона, а на другой – путешественник, дошедший до края Земли там, где небесный свод сходится с Землей, и он случайно или из любопытства проткнул посохом небесную твердь.
Когда я пошел в школу, наступило первое разочарование. Учительница сказала, что наша Земля имеет форму шара и показала глобус. Я с удивлением рассматривал глобус и обратил внимание, что он держится на подставке. У меня сразу же возник вопрос, а на чем же тогда держится земной шар. То, что Земля висит в пустоте, где нет ни верха, ни низа и падать некуда, такой ответ меня не устраивал. Когда в цирке фокусник показывает, что висящий в воздухе предмет ни на чем не держится, вы прекрасно понимаете: это всего лишь фокус и вам очень интересно узнать разгадку…
Я вспоминал разноцветные шары на новогодней елке. Они висели на нитках, привязанные к зеленым веткам. И когда я пытался представить себе красивый голубой шар Земли, одиноко висящим сам по себе, ни к чему не привязанным среди бескрайних далей космоса, я испытывал психологический дискомфорт. Меня охватывал холод одиночества.
Каждый раз у меня возникало ощущение, что по каким-то непонятным причинам мы видим не то, что есть на самом деле. За шарами планет солнечной системы прячется какая-то загадка, кроется какая-то тайна. Позади, за каждой планетой что-то есть, невидимое для нас. Космические объекты должны иметь какую-то опору, пускай не слонов и китов, как считали древние, а что-нибудь более современное. Отсутствие опоры противоестественно для нашей души. И всякий раз возникало желание исправить это неудобство. Казалось, стоит чуть-чуть напрячься и все станет на свои места, мир станет привычными миром прямых линий… Хорошо, что обычная жизнь проходила в привычном мире трех измерений. И время шло размеренно: минута за минутой, день за днем. Правда, циферблат был круглый. Но я не обращал на это особого внимания, мало ли кругов встречается в жизни. И я был очень удивлен, когда позднее узнал, что и время тоже может иметь непривычный вид. Некий ученый-физик Эйнштейн утверждал, что время может идти с различной скоростью, и оно связано с длиной, шириной и высотой. Это было невероятно: привязать минуты к сантиметрам! Это все равно, что спросить: чем рыба отличается от воды? Но больше всего меня поразила скорость света. Эйнштейн утверждал, что она имеет неизменную величину, и ничто не может ее превысить. Вы представляете себе, что значит скорость? Это же переменная величина. Вы едете на автомобиле и постоянно меняете скорость в зависимости от дорожной обстановки. И вот некий механик Эйнштейн привязал педаль газа на вашей машине так, что вы не можете ею пользоваться и стал утверждать, что это и есть скорость. И плюс к этому вы еще и никого не сможете обогнать, потому что у всех такая же скорость, как у вас. Я не люблю, когда есть что-то, чего я не понимаю. Я не люблю неопределенность. Это создает душевный дискомфорт. Везде должны быть пусть не прямые, но четкие линии, отделяющие одно явление от другого, чтобы не было все беспорядочно свалено в одну кучу. В устройстве мира должна быть какая-то логика. В таких случаях я стараюсь разобраться, что к чему, разложить все по полочкам, найти какую-то логику и успокоиться. Ведь, когда понимаешь суть вещей или событий, в душе появляется ощущение свободы. Ты как бы прозреваешь не только глазами, но и умом. Ты начинаешь понимать, какие будут последствия того или иного твоего действия и ты можешь выбирать. Ты получаешь свободу выбора. Ты получаешь пространство для маневра. Тогда приходит душевное спокойствие и уверенность в своих действиях. Но нередко бывает так, что ты не понимаешь, что творится вокруг, но разные обстоятельства, чаще всего нехватка времени, мешают вникнуть в суть проблем, и приходится жить с этим чувством непонимания. Но поскольку все эти несуразицы нашего физического мира были где-то там далеко, за пределами Земли и нашу жизнь напрямую не затрагивали, то можно было просто не думать о них до поры, до времени. Можно было отложить решение этих космических проблем до лучших времен, тем более, что существовала неотложная, почти неразрешимая проблема острой нехватки этого самого времени. С этой точки зрения можно считать благом, что бывают в жизни моменты вынужденного бездействия. Сервантес, например, написал толстый роман «Дон Кихот» сидя в тюрьме. Я тоже не от хорошей жизни оказался в ситуации, когда длительное время не мог заниматься ничем, только думать. Я тогда работал охранником в банке и, согласно инструкции не делал ничего, только анализировал ситуацию вокруг. Когда закрывались входные двери за последним клиентом, я вообще мог думать о чем угодно. Вот тогда я и решил разобраться с космическими нестыковками. Кстати, я когда-то работал в милиции и проработал там ни много, ни мало – семь лет, а эта предстоящая разборка скорее напоминала самое настоящее детективное расследование. В общем, я решил разобраться, наконец, со всем этим.
Поскольку мне предстояло разобраться с целым комплексом взаимосвязанных проблем, я решил действовать по определенной методике: брать одну какую-нибудь проблему и разбираться с ней до тех пор, пока расследование не упрется в другую нерешенную проблему, затем переключаться на решение вновь возникшей проблемы и только, решив ее, возвращаться к предыдущей. Таким образом, предполагалось неоднократное возвращение к одной и той же проблеме по мере получения новой информации. Следующий момент: я решил формулировать вопросы сразу же, как только они возникали, даже если нельзя было сразу ответить на них. Я уверен, что частоколом вопросов можно со всех сторон обложить проблему, как волка флажками, и таким образом проложить путь к ее решению. Нельзя ответить на все вопросы, но умение правильно поставить вопрос не менее значимо, чем ответ, потому что этот вопрос подсказывает, в каком направлении искать ответ. Точно также множество «нет» могут, в конце концов, указать, где прячется «да». Если на какой-то вопрос не было однозначного ответа, я решил давать несколько вариантов ответа, в том числе и заведомо дурацкие ответы. Поскольку я дилетант, мои ответы могут вызвать смех или раздражение профессионалов. Я не против смеха, я ищу истину и готов выслушать любое мнение. Когда я говорю о дурацких ответах, я имею в виду такой метод решения проблем, как брейнсторминг или мозговой штурм, когда не отвергаются никакие идеи по решению проблемы, какими бы дурацкими они не выглядели на первый взгляд. Кроме того, я решил оперировать свойствами не реального физического мира, а создать мысленную модель Вселенной и, исследуя ее свойства, сравнивать их результаты с существующими физическими законами реального мира. Модель поможет сосредоточиться на главном, опуская излишние детали. Я назвал эту мысленную Вселенную – Вселенная Хорева. Гора синай в Израйле имеет второе название – Хорев. В израйльском городе Хайфа центральный проспект носит название Хорев, а также расположенные на этом проспекте торговый и медицинский центры тоже носят название Хорев (Khorev – английский вариант написания фамилии Хорев). Так почему бы не назвать модель вселенной этой же фамилией. В этой Вселенной действуют те же физические законы. Во всяком случае, пока я в них не разобрался.
Да, я хочу сказать, что к данному моменту, когда я начинаю описывать свои мысленные эксперименты в моей мысленной Вселенной, я уже успел совершить множество погружений в этот парадоксальный космический мир и успел порядком поэкспериментировать. Я был потрясен тем, что мне открылось. Вместо спокойного, шаг за шагом познания каких-то новых свойств космоса, поиска логического объяснения того или иного явления, я каждый раз оказывался в ситуации, когда хотелось воскликнуть «Этого не может быть! Это невероятно!» У меня сложилось общее впечатление, что мир космоса – это натуральный сумасшедший дом, который находится буквально за углом наших привычных представлений о нем.
Меня не покидает ощущение, что я нахожусь в цирке, а передо мною выступает иллюзионист и показывает сногсшибательные фокусы, разгадку которых я пытаюсь отыскать.
Космос дурит нас! Алиса в стране чудес покажется наиправдивейшим повествованием после того, что я узнал о космосе! Чего только стоит, например, такой факт, что мы, оказывается, получаем информацию из космоса задом наперед, как в кино, которое киномеханик для смеха прокручивает с конца до начала. Представьте себе, допустим, такую ситуацию: небольшое дорожно-транспортное происшествие. Человек выходит на дорогу и его сбивает автомобиль. Ну, допустим, автомобиль успевает затормозить, и гражданин отделывается легким испугом, но, тем не менее, он все же падает на проезжую часть. Здесь мы видим четкую причинно-следственную связь. То есть следствием неожиданного появления пешехода перед автомобилем является то, что автомобиль его сбивает и человек падает. Начало события – выход человека на дорогу. Конец события – человек лежит на дороге, сбитый автомобилем. Так вот эту же картинку мы получим из космоса в таком виде:
1. Мы видим, что человек лежит на дороге.
2. Вот он поднимается, и от него задом отъезжает автомобиль.
3. Человек, пятясь задом, уходит с проезжей части.
Вот что нам показывает космос. Причем он делает это в непрерывном круглосуточном режиме почти с момента Большого Взрыва, а точнее, с момента появления электромагнитного излучения, то есть света.
Доказать, что космос обманывает нас в передаче информации очень просто, и я удивляюсь, что никто из ученых до сих пор не обратил на это внимания. Я расскажу об этом подробнее позднее. Это всего лишь пример одного из парадоксов космоса.
Я начал свое исследование, не подозревая, до какой степени в космосе все не так, как в нашей привычной жизни. Это совершенно другой мир. Приходится принимать правила игры, которые диктует этот «другой мир». Но каждый раз, когда я возвращаюсь в привычное пространство моей комнаты после очередного посещения этого парадоксального мира, я долго прихожу в себя, а ночью мне снится, что я запускаю собственный коллайдер на моем садовом участке или, встретив во сне себя, объясняю другому себе, что я смог вернуться в прошлое и теперь нас будет двое.
С некоторыми вещами я более менее разобрался, во всяком случае, я смог выделить и обозначить отдельные детали космического устройства. Но все-таки, по мере углубления в космические проблемы, меня не покидало ощущение, что я не ухватываю общей картины, которую составляют эти детали. Есть только ощущение, что эта картина очень своеобразная. Она в корне отличается от понимания космоса не только обычными людьми, но и учеными.
Ну, теперь уже, кажется, я все сказал.
Глава 1. Длина, ширина, высота
Начнем с простых вещей – привычных пространственных измерений: длины, ширины и высоты. На графике это так называемые декартовы координаты, оси x, y и z.
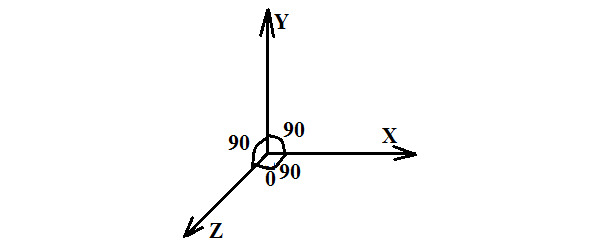
Это прямые линии, что очень радует. Но радость на этом и кончается. Настораживает то, что все три измерения существуют не сами по себе, а выходят из одной точки. Почему-то эта точка у математиков называется нулем. Хотя с моей точки зрения нуль – это ничто. Получается, что эти три линии выходят из ничего. Вот представьте теперь, что в вашей комнате «ничего» прячется в углу, причем в каждом углу. Сколько углов столько и «ничего» и все это «ничего». Если уж быть честными до конца, то нуль надо обозначать так, чтобы эти три линии не соединялись. В месте нуля должно быть действительно пусто. Вот если бы эти линии обрывались, не доходя до точки соединения, вот это действительно был бы нуль. А так, начинаются всякие домыслы. Например,
Что такое вакуум – это действительно пустота, нуль или это нечто непонятное для нас, некая загадочная форма материи?
Следующий настораживающий момент из «ничего» линии выходят под прямыми углами друг другу. Можно взять бумагу и начертить бесчисленное количество прямых линий, выходящих из одной точки. Но парадокс в том, что под прямыми углами можно провести именно только три линии: длину, ширину и высоту. Чем хорош прямой угол? Он как бы нейтрален: ни нашим, ни вашим. Конечно, прямые линии можно продолжить за пределы «ничего», тоже с прямыми углами. Они будут как бы перевернутым отражением прямых линий до «ничего», но там уже, возможно, живут ваши соседи и потому у математиков эти три линии после нуля идут со знаком «минус». А может быть у вас соседей нет, то тогда там за «ничего» прячется другой мир – может быть антимир и антивещество. Вы живете в правильном «положительном» мире,
А кто живет в «отрицательный» мире?
Вопрос про минусовую зону графика лучше сформулировать по-другому. Плюсовая зона графика соответствует нашему трехмерному физическому миру.
А может ли минусовая зона также соответствовать существованию некоей реальности, отделенной от нашего мира нулем?
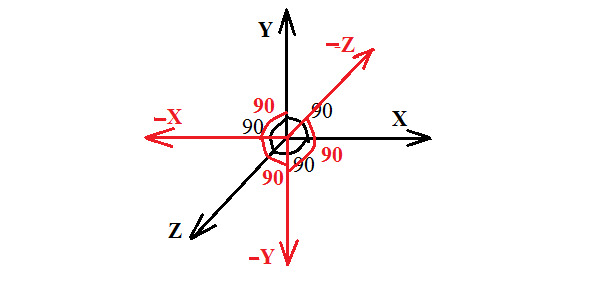
И еще один нюанс: вы положили линейку, и она лежит, лежит себе, никого не трогает, а те три линии выходят из этого самого «ничего». Они не лежат возле «ничего» они именно выходят. Здесь уже есть элемент движения. Чтобы показать это, иногда на конце этих линий рисуют стрелочки и называют их векторами. В общем, непривычные вещи начинаются буквально с первого шага.
Теперь слушайте дальше. Я был еще раз удивлен. Что же такое сами эти прямые линии? Вот как звучит математическое определение линии: «Линия – это совокупность точек». Да, да! Именно совокупность точек! Получается, что линия – это ни нечто длящееся на каком-то протяжении, а точки, выставленные в ряд. Линий, оказывается нет, а есть только точки. Опять точки, опять «ничего».
Давайте поговорим и о точке. Хотя она и обозначается нулем на декартовых координатах. Точка – это действительно нуль, реальный, настоящий нуль – это действительно ничто, то есть полное отсутствие пространства, а именно: длины, ширины и высоты. Но ведь надо же нуль как-то обозначать и математики условно обозначили его точкой. А реально все три линии упираются в нуль, в отсутствие пространства. Но вот что интересно, хотя он и нуль и ничто, он играет заметную роль в размерной Вселенной, хотя бы для контраста. Вот есть размерная Вселенная с длиной, шириной и высотой, то есть пространством. И есть нуль без длины, ширины и высоты, то есть отсутствие пространства. Мы часто будем возвращаться к нулю как обозначению отсутствия пространства. Нуль присутствует повсюду. Он как начало. Вот есть нуль – отсутствие пространства, и сразу же за ним начинается пространство: длина, ширина и высота. И я бы сказал так, что действительно, как на декартовых координатах, нуль это неразрывный элемент пространства, это начало, это точка отсчета. И, повторяю, в дальнейшем мы всегда будем опираться на это начало. Я пришел к выводу, что нуль это действительно краеугольный камень нашей Вселенной.
Скажу сразу: до начала своего расследования я ничего этого не знал. Поэтому, когда я начал штудировать учебники, и анализировать прочитанное, каждая новая страница приносила для меня новые открытия. Я хотел все поставить на свои места, но с первых же шагов стало ясно, что для того, чтобы расставить все по своим местам или разложить все по полочкам, придется подготовить новое помещение, а полки должны быть иного рода. Уж слишком непривычным открывался новый мир. И тем не менее, я хотел его понять, и во всем разобраться.
Принято считать, что наше пространство трехмерно. Оно имеет длину, ширину и высоту или другими словами: линию, площадь и объем. А точка является в буквальном смысле источником, началом трехмерного пространства. Но пока не буду отвлекаться, размышляя над этим вопросом. Продолжим разбираться с длиной, шириной и высотой. Когда в популярной литературе рассказывается о свойствах трехмерного пространства, здесь же для сравнения рассказывается, как выглядели бы двухмерный и одномерный миры, и как жители этих миров воспринимали бы различные физические явления (несчастные жители!). Считается, что наш трехмерный мир имеет объем. Соответственно двухмерный мир – это плоскость, и одномерный – линия. И опять мы скатились к точке. Точка не имеет измерений.
А мир, заключенный в точке?..
А теперь мысленно увеличим безразмерную точку до размеров шара и посмотрим, как он вписывается в пространственные измерения. В нашем трехмерном пространстве шар имеет объем. Если бы этот шар пересекал плоскость двухмерного мира, то обитатели этого мира увидели бы сначала точку, которая увеличивалась бы в размерах (этакий Большой взрыв двухмерного мира) и превратилась в увеличивающийся круг. Конечно, ученые этого двухмерного мира стали бы гадать будет ли разлет, о котором говорит «красное смещение» их пространства, продолжаться всегда или же масса круга будет достаточно велика, и он, в конце концов, станет сжиматься. А шар между тем пересек экватор и двумерные жители увидели, что он сжимается и снова превращается в точку и, наконец, он совсем исчез. В связи с этим зададим такой вопрос:
А был ли «Большой взрыв» на самом деле?..
Мы еще вернемся к проблеме пересечения плоскости шаром и к самому шару, а заодно и кругу или окружности. А пока вернемся к описанию двухмерного и одномерного пространств. Гипотетические обитатели двухмерного мира будут воспринимать шар как круг. А если их плоский мир будет пересекать другая плоскость, они буду воспринимать ее как линию. Соответственно в одномерном пространстве шар будет восприниматься как линия, а линия – как точка. Мы знаем теперь, как воспринимали бы жители двухмерного и одномерного пространств шар и плоскость, пересекающих их ограниченные миры. А теперь назовем этих жителей наблюдателями. Наблюдатель всегда находится вне наблюдаемого объекта, даже если он физически находится внутри объекта, допустим, того же шара или же рассматривает свои внутренности через микроскоп. Наблюдатель отличается от наблюдаемого объекта. Его отделяет от наблюдаемого объекта четкая граница иначе бы он просто не мог отделить себя от того, что он наблюдает. Поскольку наблюдатель видит глазами (в крайнем случае – воспринимает органами чувств), то наблюдаемый объект должен находиться перед глазами – вне наблюдателя. Я согласен, что жители плоского мира воспринимали бы шар, как круг… на ощупь, но видели бы они только линию – отрезок, меняющий размеры. Это мы, жители трехмерного мира видим, что они имеют дело с кругом. А теперь спросим себя: что видят жители одномерного мира, когда их линию пересекает шар? Если они находятся с двух сторон шара, то они сообщают друг другу, что какой-то все удлиняющийся, а потом все укорачивающийся отрезок перегораживает их путь, но при этом каждый из них видел бы только точку. То есть и те и другие видят на одно измерение меньше того пространства, где они живут. Тогда зададим себе такой вопрос:
Где живем мы, если мы видим на одно измерение меньше?..
И второй вопрос:
Откуда мы смотрим на наш внешний трехмерный мир?
Итак, мы видим на одно измерение меньше того пространства, в котором мы живем. Сначала я подумал, что сделал открытие: что мы жители трехмерного мира смотрим из некоего четвертого измерения на наш трехмерный мир. Но потом, проанализировав, что же собственно мы видим, я пришел к выводу, что мы не видим объема, мы всегда видим плоскость, то есть два измерения. Куб всегда представляется нам плоским, и только стереоэффект двух глаз формирует объем. Ну, а теперь еще раз задумаемся: может быть наш мир двухмерен? Мы всегда шагаем, едем, плывем по плоскости, по поверхности чего-либо. Что такое высота? Это гравитация. Земное притяжение дает нам указание, что плоская стена перед нами – это третье измерение, то есть высота, а если бы не было гравитации, мы бы и стену воспринимали как плоскость и также ходили бы по ней. Даже человек внешне представляет собой плоскость – это его кожный покров. Получается, что мы все-таки живем не в трехмерном (время пока не будем учитывать), а двумерном мире и видим не трехмерный, а двумерный мир. Если бы мы видели три измерения, мы бы видели и обратную сторону куба, но тогда бы мы были обитателями не трехмерного, а четырехмерного пространства, а я пока не нашел убедительных доказательств, что дополнительные размерности это такие же линии, как длина, ширина и высота. Возьмем, например, такую размерность, как время. Для него, оказывается, тоже есть линия на графике. Это диагональ, тоже выходящая из нуля.
В связи с этим у меня есть претензии к способам измерения нашего физического мира. Как я уже сказал, фактически высота – эта та же самая плоскость, поставленная вертикально. А что скрывается там, под поверхностью этой самой плоскости? Возьмем лучше не высоту, а толщину. Толщина – это материал, внешней границей для которого является плоскость. Мы обычно не видим этот материал, плоскость скрывает его от нас, служит границей. Если мы даже разломаем плоскость, что мы увидим в месте разлома? Опять плоскость. Она будет неровной, но это не меняет дела. Под этой плоскостью скрыта не толщина, а суть предмета. Это может быть железо, камень, пластик. Каждый предмет будет состоять из других атомов. Мы можем увидеть их в электронный микроскоп. Ну и что? Мы опять увидим плоскую поверхность шара, вернее шаров. Но мы не увидим сути.
Так вот, третьим или следующим измерением надо бы назвать суть физического тела, которая скрывается под плоскостью, но проблема в том, что неизвестно в каких мерках измерять суть? И что собственно назвать сутью предмета? В чем, например, суть железной болванки? Может быть это функции той вещи, того материального объекта, которые измеряются с внешней стороны в сантиметрах и метрах. То, что заставляет вещь функционировать, можно измерить лишь косвенно, фиксируя проявления функции в нашем материальном, плоском мире. И еще один момент. Кто-то извне должен выяснять суть вещи, предмета. Должен быть еще один предмет, вещь, а проще говоря, некий наблюдатель, который бы оценивал не только внешнюю сторону предмета, но и его суть. Сам предмет не будет выяснять свою суть. Получается, что наблюдатель – неотъемлемое добавление к любому предмету, вещи, а если глубже, то и явлению, неотъемлемый внешний фактор, который помогает определять суть окружающей его действительности. Получается, что наблюдатель – это еще одно измерение, дополнительное к сути предмета. Получается, что мир существует для наблюдателя, что наблюдатель – неотъемлемая часть существующего мира. Наблюдатель не видит саму суть предмета. Он определяет ее опосредованно через функции предмета. Хотя функции у вещей, предметов, явлений разные, но всех их можно объединить одним определением – идея вещи или явления. Парадокс здесь заключается в том, что само это третье измерение невозможно измерить. Оно не имеет измерений. Оно везде, и в тоже время оно где-то заложено изначально. Материальные характеристики определяют различие проявлений идеи в нашем мире, но суть ее одна, она оживляет наш мир, приводит его в движение. В духовном отношении мы сами части этой идеи, поэтому мы не можем видеть идею, а только ее проявления. Мы смотрим оттуда. Мы не можем видеть то, частью чего мы являемся. Мы – дети двух миров. Наша оболочка принадлежит материальному плоскому миру, наша душа принадлежит недоступному для нашего обзора третьему измерению.



