
Полная версия
Набор инструментов для управления проектами
Преимущества и недостатки. Главное преимущество экономических методов состоит в том, что они относительно открыты. Как и в случае любого капиталовложения, основной их недостаток – необходимость наличия информации о будущих расходах и доходах. Эти данные не только сложно получить, они также подвержены значительной неопределенности.
Резюме
В настоящем разделе представлены три экономических метода отбора проектов: время окупаемости, чистая приведенная стоимость и внутренняя норма прибыли. Они применимы главным образом к капитальным проектам и проектам, предназначенным для улучшения существующих или разработки новых продуктов. Экономические методы допускают прямое сравнение таких проектов с альтернативными способами вложения средств. Они легки для понимания, а их расчет прост – при условии, что получены все необходимые данные. Во врезке «Контроль экономических методов» мы еще раз отметим ключевые положения, касающиеся применения экономических методов.
КОНТРОЛЬ ЭКОНОМИЧЕСКИХ МЕТОДОВ
Контроль позволяет убедиться в том, что экономические методы применяются надлежащим образом. Здесь необходимо:

Методы выбора портфеля
Что такое методы выбора портфеля?
Методы, представленные в предыдущих разделах, рассматривали каждый проект изолированно, без учета его взаимодействия с другими проектами. Однако могут существовать факторы, ограничивающие выбор проектов, в частности бюджет, ограничения по персоналу, по поддержке выполняемых операций (возможности опытного производства, машинное время), и другие соображения, такие как политика компании. Для решения этих вопросов следует использовать методы выбора портфеля проектов [7], которые учитывают все подобные ограничения.
Применение методов выбора портфеля
Сначала необходимо собрать исходную информацию:
• данные о проектах-кандидатах;
• политики компании.
Первый шаг в применении методов выбора портфеля заключается в идентификации (определении) проектов, которые являются кандидатами на включение в портфель. Следующий этап – сбор данных о каждом из проектов-кандидатов. Данные должны включать в себя те аспекты, которые отражают возможные конфликты или взаимодействия между проектами. Перекрытие требований к ресурсам, политики компании относительно типов проектов, включаемых в портфель, и другие соображения, которые могут ограничить выбор, следует включить в рассмотрение.
Конструирование модели портфеля. Проанализируем меню проектов, представленное в табл. 2.6. В дополнение к критериям выбора, использованным в примерах модели ранжирования проектов или аналитического иерархического процесса, примем во внимание взаимодействие проектов, чтобы получить портфель без конфликтов. Предположим, что бюджет ограничен величиной 600 тысяч долларов, максимально доступное время опытного производства составляет 4500 часов, а максимально доступное машинное время – 700 часов. Исходя из этих сведений, нужно составить такой портфель проектов, который обеспечит максимальную отдачу.
Электронные таблицы, например Excel, могут выполнить подобную «оптимизацию» в случае проблемы небольшого масштаба. В табл. 2.7 показана таблица Excel, предназначенная для отбора проектов в портфель и обеспечивающая максимальную отдачу при отсутствии нарушения какого-либо ограничения. Значение «1» в столбце «Выбран» означает, что данный проект был отобран для включения в портфель, значение «0» – наоборот. Запись в ячейке «Общая стоимость» представляет собой встроенную в Excel функцию SUMPRODUCT, примененную к столбцам «Выбран» и «Стоимость». Аналогичная операция проведена и для ячеек «Время опытного производства» и «Машинное время».
Как только проблема сформулирована, с помощью Excel SOLVER (или эквивалентного модуля в случае другой таблицы) легко рассчитать оптимальный портфель. Очевидно, что значения «Общая стоимость», «Время опытного производства» и «Машинное время» здесь удовлетворяют наложенным ограничениям. Оставшиеся ограничения нуждаются в объяснении. В частности, мы не хотим, чтобы программа пыталась «купить» ресурсы, выбирая «отрицательный проект». Следовательно, значения в столбце «Выбран» не должны превышать 1. И наконец, мы не вправе выполнить только половину проекта, следовательно, значения в столбце «Выбран» должны быть целыми. Три названных ограничения, действующие совместно, приводят к тому, что ячейки в столбце «Выбран» могут принимать два значения: 0 и 1. Другими словами, отбираться могут только целые проекты и не более чем по одному за раз (28).
Возможна ситуация, когда в списке проектов-кандидатов появятся две версии одного проекта: «аварийная» и «нормальная». Чтобы выбрать одну из этих версий, нужно добавить следующее ограничение:
X + Y ≤ 1,
где X и Y – ячейки столбца «Выбран», соответствующие двум версиям одного и того же проекта.
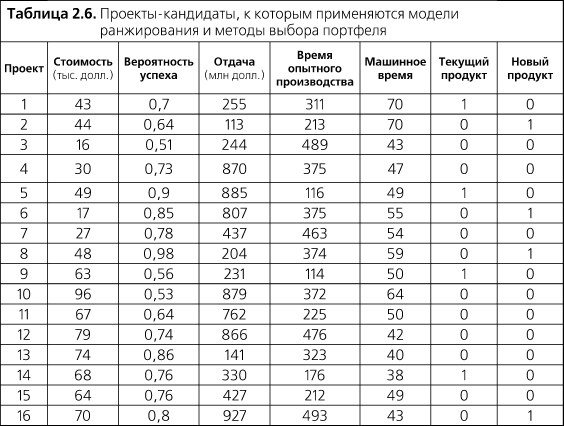
Предположим далее, что согласно политике компании как минимум один проект должен поддерживать новый продукт и как минимум один – текущий продукт. В некоторых ячейках двух крайних правых столбцов таблицы присутствует значение 1, показывающее, поддерживает проект новый или существующий продукт либо не связан с продуктом (например, проект совершенствования производственных процессов). Допустимо добавить ограничения, согласно которым функция SUMPRODUCT столбца «Текущий продукт» и SUMPRODUCT столбца «Новый продукт» со столбцом «Выбран» должны равняться или превышать 1. В предыдущем примере это не изменило бы результат, поскольку проекты, которые поддерживают существующий и новый продукты, уже отобраны. Однако в иной ситуации, если добавить подобные ограничения, в результирующий набор были бы включены другие проекты. Результатом, скорее всего, явилось бы уменьшение общей отдачи при соблюдении политики компании.
В приведенном примере бюджет оказался основным ограничением. Проекты, отобранные в портфель, потребляют почти все выделенные средства, зато имеется значительный запас по времени опытного производства и машинному времени. Это открывает ряд возможностей по проверке чувствительности. Насколько возросла бы общая отдача, если увеличить общий бюджет проекта? Не важно, какое ограничение является основным, – использование оптимизирующих возможностей электронной таблицы позволяет менеджеру понять, какую дополнительную прибыль можно получить, если ослабить определяющее ограничение, и, наоборот, какую прибыль можно потерять, если сделать его более сильным.
Использование метода выбора портфеля
Когда использовать. Метод выбора портфеля удобен, если имеют место многочисленные ограничения, накладываемые на отбор проектов в портфель (см. врезку «Советы по использованию метода выбора портфеля»). Поскольку для выполнения оптимизации необходима та или иная мера финансовой отдачи, лучше всего задействовать этот метод в том случае, когда нужно получить максимальную прибыль. Однако он может использоваться и для тех типов проектов, которые не подразумевают непосредственную генерацию прибыли. Например, список проектов-кандидатов может включать в себя численные показатели их достоинств, полученные с помощью модели ранжирования проектов или аналитического иерархического процесса. Затем допустимо применить метод выбора портфеля, чтобы максимизировать суммарный показатель достоинств всех проектов с учетом ограничений по бюджету, обеспечению персоналом, поддерживаемым операциям и другим ресурсам. Таким образом, показатель, который нужно улучшить, не обязательно должен представлять собой финансовую прибыль – это может быть любой параметр, являющийся мерилом «хорошести» (29) проекта.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Примечания
1
Журнал «Fortune» (США) ведет ежегодно обновляющийся список 500 крупнейших компаний США, ранжированных по объему продаж. – Прим. ред.

