
Полная версия
Философия. Античные мыслители
1. В чем особенность теоретического знания? Как оно связано с понятием свободы?
2. Почему математическое доказательство появляется вместе с теоретическим знанием?
3. Почему ясность предполагает знание начал?
4. Приведите аргументы Анаксимандра (воспроизведенные Аристотелем) в пользу того, что начало должно быть беспредельным.
5. Какая трудность возникает из-за того, что начало всего – беспредельное.
6. Почему всеобщая текучесть делает знание невозможным?
7. Что представляет собой бытие в понимании Парменида? Приведите его основные аргументы.
8. В чем различие знания и мнения у Парменида?
9. Объясните логическую структуру апорий Зенона.
Глава 2
Пифагорейская школа
Пифагора можно считать младшим современником Анаксимандра[31]. Именно он, как утверждают источники, стал впервые называть свое учение философией (т. е. любовью к мудрости). Человек, по его утверждению, слишком слаб, чтобы обладать самой мудростью, но может лишь стремиться к ней. Однако говорить мы далее будем не о самом Пифагоре, а о его школе. Отметим, кстати, что мы сталкиваемся здесь с замечательным явлением в истории мысли: созданием философской школы, т. е. философского движения, на протяжении нескольких столетий объединявшего многих единомышленников. Конечно, пифагорейская школа менялась в течение своей долгой истории. Сейчас мы будем говорить о ее раннем периоде, т. е. до IV в. до н. э., однако для пояснения основных идей будем прибегать и к более поздним источникам. Вопреки принятой традиции, мы обсуждаем учения ранних пифагорейцев после разговора о Гераклите и Пармениде. Это кажется уместным, поскольку названные авторы, судя по всему, повлияли на пифагорейских мыслителей, о которых мы сейчас будем говорить. Более того, в дошедших до нас пифагорейских текстах, возможно, содержится некоторая полемика как с Парменидом, так и с Гераклитом.
В этом разговоре нам не избежать экскурсов в разнообразные исследования, проведенные пифагорейцами в арифметике, геометрии, астрономии, музыке, а также других науках. Эти исследования вели и другие мыслители, в том числе Фалес, Анаксимандр, Гераклит и Парменид, о которых мы здесь уже писали. Однако именно у пифагорейцев намечается некая система знаний, т. е. попытка сведения всего к единым основаниям. Можно сказать, что у них намечается нечто вроде дедукции всех наук из начал. Поэтому в пифагорейской науке можно (по-видимому впервые) конкретно проследить, что представляет собой ясное знание и как оно получается.
Мы видели, что Парменид полагает различие бытия и небытия контрадикторным: можно либо быть, либо не быть. Контрадикторны также предел и беспредельное, т. е. первый соответствует бытию, а второе – небытию. Во фрагментах Филолая[32] мы видим попытку смягчить это противопоставление. Выражаясь языком классической логики, оно оказывается не контрадикторным, а контрарным. Между двумя противоположностями находится нечто третье. Предел и беспредельное Филолай рассматривает как два начала, к которым причастны все вещи. Иными словами, все сущее, открытое нашему взгляду и доступное нашей мысли, есть единство предела и беспредельного, содержит в себе и то и другое. А. Ф. Лосев приводит весьма выразительный фрагмент Филолая:
Все существующее должно быть пределом или беспредельным или тем и другим вместе. Но быть пределом или только беспредельным оно не может. Вследствие того, что, как оказывается, оно не состоит ни исключительно из одного предела, ни исключительно из одного беспредельного, совершенно ясно, что мировой строй и [все], что в нем, образовалось из соединения предела и беспредельного и наглядным примером этого может служить то, что наблюдается в действительности на полях: а именно, одни части их, состоящие из самых границ [т. е. межи], ограничивают [участки], другие же части, состоящие из границ и [лежащих за последними] неограниченных [участков], ограничивают и не ограничивают, те же, которые состоят [только] из неограниченного [пространства], будут являться неограниченными (курсив А. Ф. Лосева. —Г. Г.)[33].
Следовательно, во всем, что существует, мы должны обнаружить присутствие того и другого. Кажется, что это вполне соответствует и нашему обыденному опыту. Конечно, все, что нас окружает, изменчиво и множественно. Наши суждения, пытающиеся уловить что-либо из видимых вещей, неточны, наши познания далеки от ясности. Но все же трудно согласиться с Парменидом и признать их лишь ложью, а все вещи – призраками. Все же мы улавливаем какую-то определенность, какие-то относительно устойчивые формы. Поэтому мысль о единстве двух начал кажется вполне уместной. Но как возможно такое единство? Филолай обнаруживает здесь серьезную трудность. Вещи «неподобные, неединородные» не могут соединиться и создать нечто упорядоченное[34]. Но предел и беспредельное именно таковы. Следовательно, должно существовать нечто их объединяющее, удерживающее вместе два разнородных элемента. Это удерживающее или скрепляющее начало Филолай называет гармонией.
В привычном нам употреблении слово «гармония» принадлежит к теории музыки и обозначает правильное сочетание тонов в созвучии. Взятое в более широком значении оно может работать как эстетическая категория, выражающая стройную согласованность частей в рамках упорядоченного целого. Заметим, что буквальное значения греческого слова harmonia – связь, скрепа[35]. Пифагорейская философия сочетает все три значения, при этом исходит она, по-видимому, из теории музыки. Это понятие было затем воспринято Платоном и его многочисленными последователями. Учение о гармонии неотделимо от всякого рассуждения о порядке, структуре, организации частей в пределах целого. Поэтому я намерен рассмотреть некоторые детали пифагорейской теории музыки.
2.1. Пифагорейская теория музыки
Пифагорейцы строят свою музыкальную теорию на опытных фактах, которые, однако, оказываются лишь материалом для глубоких теоретических (прежде всего математических) исследований. Исходное наблюдение состоит, по-видимому, в том, что звуки (например звуки, извлекаемые с помощью музыкальных инструментов) имеют разную высоту[36]. Например, зажимая натянутую струну в разных местах, мы можем делать ее звучание более высоким и более низким. Взяв два звука разной высоты, мы, по крайней мере теоретически, можем найти звук промежуточной высоты, т. е. выше более низкого, но ниже более высокого. Так можно сделать для любой пары различных по высоте звуков. Следовательно, можно представить себе непрерывную шкалу высот: любая пара звуков заключает внутри себя бесконечный интервал звучаний. Хотя наше ухо не может уловить различия между звуками, достаточно близкими по высоте, но теоретически мы в состоянии вообразить, что звуки могут приближаться друг к другу по высоте сколь угодно близко, сохраняя, однако, различие. Таким образом, каждый звук есть точка, извлеченная из континуума различающихся по высоте звуков.
Такое представление уже указывает на соединение предела и беспредельного. Континуум звуков беспределен. Однако, извлекая отдельные звуки на музыкальном инструменте, мы находим на этом континууме определенные точки, выделяем в нем некоторые интервалы, т. е. задаем границы, пределы. Представим себе, например, восьмиструнную греческую лиру. Две крайние струны, издающие самый высокий и самый низкий для этого инструмента звук, как бы вычленяют определенный интервал из беспредельного множества звуков, неограниченного по высоте ни сверху, ни снизу. Однако заданный двумя струнами интервал также беспределен. Он хотя и ограничен сверху и снизу, но безгранично делим и содержит бесконечно много звуков. Другие струны лиры задают целую систему границ, устанавливая новые пределы, упорядочивая континуум звучаний. Рассмотрим подробнее, как осуществляется это упорядочение.
Приведем еще один эмпирический факт: существует интервал, такой, что разделяемые им звуки звучат как будто одинаково, несмотря на различие в высоте, а при одновременном звучании сливаются в один голос. Такое звучание называют по-латыни консонанс. Именно так настраивались две крайние струны восьмиструнной лиры, а потому и интервал получил впоследствии название октава.
В пределах октавы выделяется еще два консонансных интервала, получивших названия квинта и кварта. Разделяемые ими голоса также сливаются в один, но не так точно и совершенно, как в октаве. При этом квинта звучит все же более согласованно, чем кварта.
Три консонансных интервала определенным образом организуют звуковой континуум. Чтобы увидеть это, представим три голоса – обозначим их А, С, D. Пусть интервал между А и D составляет октаву, а между А и С – квинту. Все три голоса будут создавать консонанс. При этом оказывается (также эмпирический факт), что интервал между С и D составляет кварту. Оказывается, таким образом, что октава представляет собой сумму двух других консонансных интервалов. Взяв далее еще один звук – В – образующий с А кварту, мы установим в пределах октавы некоторую систему интервалов. Звук В отличается от D на квинту. Октава оказывается разделена на последовательность интервалов четырьмя голосами: А, В, С, D. Интервалы между этими голосами графически изображены на рис. 1.
Обратим внимание на интервал ВС. Он образует как бы недостающую часть, которую надо добавить к двум квартам, чтобы получилась октава. Он же составляет разницу между квартой и квинтой. Этот интервал называется тон. Хотя сам он не дает никакого созвучия, ему можно приписать весьма важную роль. Он составляет меру для всех музыкальных интервалов. Любой воспроизводимый в музыке интервал составлен из тонов (в некоторых случаях из полутонов).
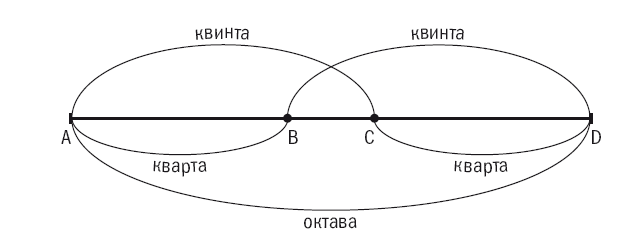
Рис. 1. Схема соотношений интервалов звука
Таким образом, в беспредельный континуум звуков внесены не только границы, но и внутренняя соразмерность. Возникает возможность точного числового соотнесения интервалов. Более того, консонансные интервалы представлены как соразмерные части организованного целого. Однако эта организация еще не вполне прояснена. Слишком много в ней основывается на чувственном восприятии, на способности человека различать и соотносить звуки. Ясно, что эта способность у всех различна, а отношения, основанные на таком восприятии, не могут быть точными. Пифагорейцы постарались найти для своих исследований более надежную опору, что и привело к исследованию музыкальной гармонии.
Главным открытием пифагорейцев в теории музыки следует считать то, что они сумели свести звуковые интервалы к отношениям длин, т. е. весьма точно измеряемых величин. Эти отношения собственно и получили названия гармоний.
Сохраним те обозначения, которые мы только что использовали, только теперь буквами А, В, С, D будем обозначать не сами звуки, а длины струн, которые эти звуки производят. Пифагорейцам принадлежит следующее открытие.
Октава соответствует отношению 1:2, т. е., если звук D на октаву выше А, то струна D в два раза короче струны А.
Соответственно отношения длин струн А к В составляет 4:3 (кварта).
Отношение А к С составляет 3:2 (квинта).
Иными словами, каждый консонансный интервал определяется числовым отношением. Присмотримся к этим
отношениям внимательнее. Чтобы лучше описать их свойства, разделим А на 12 равных частей. В таком случае двенадцатая часть А окажется единицей измерения, т. е. общей мерой для всех остальных струн. Легко видеть, что при измерении этой единицей А=12; В = 9; С = 8; D=6. Получается, что отношение С к D составляет 4:3, а отношение В к D – 3:2, что, как и следовало ожидать, соответствует кварте и квинте.
Легко видеть, кроме того, что один тон определяется отношением В к С, т. е. 9:8. Это значит, что можно строить и другие звуковые интервалы. Выбрав тон в качестве меры для интервала звучаний, можно подобрать требуемые отношения длин для любого интервала в пределах октавы. При этом всякий раз будет сохраняться соразмерность длин. Правда использовать двенадцатую часть А (самой длинной струны) в качестве общей меры уже не удастся. Всякий раз нужно будет выбирать другую единицу измерения. Тот факт, что именно для трех консонансных интервалов существует общая мера, как будто говорит об их особой природе.
Итак, консонансные звучания определяются числовыми пропорциями. Эти пропорции пифагорейцы и назвали гармониями, т. е. скрепами. Именно они, по мысли Филолая, скрепляют предел и беспредельное. В самом деле, с помощью числовых отношений структурируется беспредельность континуума звуков, вносится порядок, определенность, устойчивость в то, что поначалу предстает как неопределенное, неуловимое. Существование числовых отношений, в свою очередь, определяется соизмеримостью, т. е. наличием общей меры. Величины, соответствующие звукам, измеряются одной и той же единицей, что и создает их особую связь друг с другом. Все они могут быть представлены как части, складывающиеся в некоторое целое: каждая из величин В, С или D составляет часть А, причем часть, соразмерную с целым[37].
2.2. Пифагорейская космология
Космология пифагорейцев построена на тех же основаниях, что и теория музыки. Впрочем, здесь, наряду с наблюдениями за движением светил, они прибегают и к весьма произвольным построениям, позволяющим им перенести на Космос те самые числовые гармонии, которые они открыли, исследуя музыку. Важно, что и в космологии речь идет о пределе и беспредельном и об их соединении с помощью числа.
Обратим внимание на два свидетельства о пифагорейской космологии. Утверждается, что Пифагор первым назвал Вселенную «космосом», имея в виду порядок, который ему присущ[38]. Аристотель же описывает пифагорейское представление о космосе так:
Пифагорейцы также признавали существование пустоты и утверждали, что она проникает в Небо [=космос] из [окружающего] бесконечного (ἄπειρον), как если бы [Небо] вдыхало пневму и пустоту, которая разграничивает физические сущности (φύσεις), как если бы пустота была разделением и разграничением смежных [тел]. Прежде всего, это наблюдается в числах, так как пустота разграничивает [их, сообщая] им самобытность (φύσις) (Аристотель. Физика. Δ. 6. 213 b 22)[39].
Итак, Вселенная есть космос, т. е. некоторый порядок. Однако этот порядок существует наряду с неопределенностью, с беспредельностью, пустотой. Беспредельность и пустота не только объемлют космос, но и проникают внутрь него. Что означает проникновение пустоты внутрь порядка? Я думаю, это можно понять по аналогии с только что рассмотренной теорией музыки. Мы видели, что музыкальная гармония вносит упорядоченность в континуум звуков. Отдельные («точечные») звуки, ограничивающие интервалы и образующие консонанс, создают определенную структуру, порядок, определяемый числовыми отношениями. Однако эта структура, во-первых, объемлется неупорядоченным континуумом звуков, а во-вторых, наполнена им изнутри. Как бы мы ни ограничивали музыкальные интервалы, создавая упорядоченную звуковую структуру, между границами всегда будет оставаться континуум, бесконечная, неупорядоченная совокупность потенциальных звуков.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Примечания
1
Из вышедших в последние годы на русском языке книг хотелось бы порекомендовать французский двухтомник 1997 г. под редакцией М. Кан-то-Спербер (рус. пер.: Греческая философия: В 2 т. М.: ГЛК. Т. I. 2006. Т. 2. 2008).
2
Ахутин А. В. Античные начала философии. СПб.: Наука, 2007. С. 12.
3
Мы не случайно до сих пор используем для ее наименования все то же греческое слово!
4
В свое время эта идея была убедительно представлена Э. В. Ильенковым в статье «Школа должна учить мыслить!» (1964). См.: Ильенков Э. В. Школа должна учить мыслить. М.: МПСИ, 2002. С. 6–55.
5
От греч. doxa – мнение.
6
Фалес, по свидетельству Диогена Лаэртского родился в первый год тридцать пятой олимпиады (640 г. до н. э.), а умер в возрасте 78 лет. См.: [Фрагменты, 103]. О том, что он является автором первого математического доказательства, свидетельствует Евдем Родоссский. См.: [Зайцев, 209].
7
Если при ссылке на источники не указано конкретное издание, то речь идет об изданиях, которые представлены в специальном разделе списка литературы в конце данного учебника. – Прим. ред.
8
[Фрагменты, но].
9
Не исключено, впрочем, что автор приводимого свидетельства (Гераклит-Аллегорист) допускает здесь анахронизм, приписывая Фалесу мысль о четырех стихиях. Эта концепция, по-видимому, сформировалась позже.
10
О времени жизни Анаксимандра можно судить по утверждению Диогена Лаэртского, что во второй год 58-й олимпиады (т. е. в 547 или 546 г. до н. э.) ему было 64 года.
11
См[Фрагменты, 117].
12
Их расцвет (т. е. возраст, равный примерно 40 годам) приходится на 69 олимпиаду (504–501 гг. до н. э.). См.: [Фрагменты, 176, 274].
13
Цш. по: [Фрагменты, 209].
14
д. Цит. по: [Фрагменты, 211].
15
ю. Несколько иной перевод этого отрывка см. также в: [Фрагменты, 551].
16
[Фрагменты, 211–212].
17
[Фрагменты, 195].
18
[Диоген Лаэртский, 333]. В книге «Фрагменты ранних греческих философов» это место переведено иначе: «Мудрым можно считать только одно: Ум, могущий править всей Вселенной» [Фрагменты, 176].
19
[Фрагменты, 217].
20
С заглавной буквы здесь и далее пишутся термины-названия тех «сущностей», что существуют в единственном числе.
21
[Фрагменты, 189].
22
[Фрагменты, 197].
23
Их двоих, а также Мелисса называют элеатами, как выходцев из греческой колонии Элея (в Италии).
24
[Фрагменты, 286–298J.
25
[Фрагменты, 291].
26
Этот оборот использовал по схожему поводу Платон в диалоге «Тимей», о чем мы будем подробно говорить в главе 5.
27
[Фрагменты, 297].
28
[Фрагменты, 291].
29
[Фрагменты, 296]. Приведем другой перевод этого места: «Одно и то же – мышление и то, о чем мысль» [Фрагменты, 291].
30
Всего до нас дошли 9 апорий. Их разбор см., напр.: [Маковельский, 475-53б\.
31
Его расцвет приходился на 6о олимпиаду (540–537 гг. до и. э.).
32
Утверждается, что был первым из пифагорейцев, написавшим книгу. См.: [ДиогенЛаэртский, 330].
33
[Лосев 1963, 266]. Я даю перевод, использованный Лосевым, поскольку он выглядит более прозрачным, чем перевод этого же места в книге: [Фрагменты]. Для сравнения приведу его здесь: «Все сущие по необходимости должны быть либо ограничивающими, либо безграничными, либо и ограничивающими и безграничными [одновременно]. Но быть только безграничными или только ограничивающими они не могут. Стало быть, так как очевидно, что они не [состоят] ни из одних лишь ограничивающих, ни из одних лишь безграничных [элементов], то, следовательно, ясно, что и космос и вещи в нем были слажены из ограничивающих и безграничных [элементов]. Это явствует из того, что [наблюдается] в произведениях: те из них, что из ограничивающих, ограничивают, те, что из ограничивающих и безграничных, ограничивают и не ограничивают, а те, что из безграничных, окажутся безграничными» [Фрагменты, 441\.
34
См\Фрагменты, 442\.
35
Интересно, что слова «гармония» и «арматура» происходят от одного корня.
36
В рассмотрении музыкальной теории пифагорейцев я опираюсь на исследование: [Щетников 2012].
37
Уместность разговора о целом и частях обнаружится, если мы будем рассматривать не четыре струны разной длины, а одну струну, которая пережимается в разных местах. Пережав А посередине, мы получим октаву, разделив точкой пережатия в отношении 3:1, заставим большую часть звучать в кварту с целым и т. д.
38
Псевдо-Плутарх. Мнения философов. 2.1.
39
Цит. по: [Фрагменты, 482]. В переводе В. П. Карпова этот фрагмент звучит несколько иначе: «Пифагорейцы также утверждали, что пустота существует и входит из бесконечной пневмы в само Небо, как бы вдыхающее [в себя] пустоту, которая разграничивает природные [вещи], как если бы пустота служила для отделения и различения смежных [предметов]. И прежде всего, по их мнению, это происходит в числах, так как пустота разграничивает их природу» (см.: Аристотель. Сочинения: В 4 т. Т. 3. М.: Мысль, 1981. С. 136).


