
Полная версия
О чем рассказали «говорящие» обезьяны: Способны ли высшие животные оперировать символами?
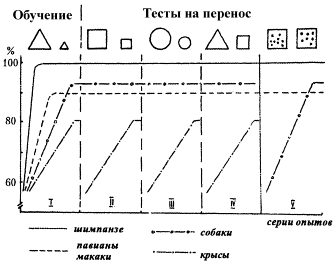
Независимо от этих авторов, работавших с птицами, тот же критерий предложил и Л. А. Фирсов. В его опытах шимпанзе сначала обучали выбирать геометрические фигуры большей площади. Затем проводили серию тестов на перенос, и они с первого же раза правильно выбирали большую в паре новых фигур, продемонстрировав допонятийное обобщение по признаку «больше по площади». После этого им предъявили стимулы другой категории – разное число точек, и они без дополнительного обучения выбирали стимул с бóльшим числом элементов, показав, что применяют сформированное обобщение также в отношении числа раздражителей (другая категория признаков), т. е. оно превратилось в обобщение «больше вообще», или «мера» (рис. 6).
Довербальные понятия – высший уровень обобщения у животных
Именно такой перенос и расценивают как показатель формирования довербального понятия (Фирсов 1972, 1982, 1993). В этом случае животное, по-видимому, переходит от наглядно-образной к более абстрактной, хотя и невербальной форме обработки и хранения информации, когда отражение действительности происходит на уровне понятий, не опосредованных словом.
Способность применения правила выбора, сформированного в отношении стимулов одной категории («выбирай сходный по цвету»), к стимулам другой категории («выбирай сходный по форме, или по числу элементов, или др.»), обнаружена у приматов (Фирсов 1993; Фирсов, Чиженков 2003), прежде всего человекообразных, у дельфинов, а также у врановых (Зорина и др. 2001; Koehler 1956; Wilson et al. 1985) и попугаев (Pepperberg 1987a, b; 1999/2002). Интересно отметить, что по этим данным Л. А. Фирсова собаки не способны к формированию довербальных понятий, как и (по данным нашей лаборатории) к решению задачи на оперирование размерностью (Дашевский 1979; Дашевский, Детлаф 1974; Крушинский 1986) и некоторых других когнитивных тестов. Обобщив признак «больше по величине» при выработке дифференцировки фигур разной площади, они в отличие от шимпанзе и макак и капуцинов не смогли перенести эту реакцию на стимулы другой категории – различающиеся по числу элементов.
Таким образом, способность к обобщению распространена у разных видов позвоночных (она есть даже у черепах), однако наиболее развитой она оказывается у человекообразных обезьян.
Изучение способности животных к символизации в традиционных лабораторных экспериментах на примере «счета» (обобщения признака «число»)
Способность некоторых животных к высокой степени обобщения позволяла предположить, что им доступна и способность к усвоению и использованию символов, т. е. та когнитивная операция, которая составляет основу речи человека.
Символизацией называют процесс установления эквивалентности между ранее нейтральными для субъекта стимулами и соответствующими предметами, действиями, а также обобщениями разного уровня, в результате которого появляется возможность оперировать ими как символами в полном отрыве от обозначаемых предметов, действий и обобщений.
Обобщение числовых признаков, или «Счет» у животных
Для изучения способности животных к символизации применяют разнообразные экспериментальные приемы. Один из них связан со способностью обобщать признак «число» и связывать представление о числе с символами-цифрами. Доказано, что животные выполняют разного рода количественные оценки параметров среды, включая формирование довербального понятия о числе (например, Boysen 1993; Brannon, Terrace 2000; Biro, Matsuzawa 2001). На следующем этапе анализа выясняют, могут ли животные связывать это понятие с символами (например, арабскими цифрами), т. е. существуют ли у них зачатки способности к «истинному счету» с помощью числительных, которой в полном объеме наделен только человек.
Вопрос о наличии у животных зачатков «истинного счета» и критериях, которым они должны удовлетворять, составляет предмет острых дискуссий (см. Davis 1993; Davis, Perusse 1988; Gallistel 1990). Поскольку в качестве универсального стандарта рассматривают «человеческий счет» с помощью символов (числительных), прежде всего необходимо отметить, что этот термин подразумевает процесс формальной нумерации, используемый людьми для определения абсолютного числа элементов в множествах.
Р. Гельман и К. Галлистель (Gelman, Gallistel 1978) предложили ряд критериев, которые необходимо учитывать при оценке способности животных использовать символы для маркировки множеств. Наиболее важные из них:
• каждому пересчитываемому элементу должен соответствовать индивидуальный символ (принцип «соответствия один к одному»);
• символы должны в стабильном порядке соответствовать пересчитываемым элементам (принцип «ординальности» – использование цифр как порядковых числительных);
• символ, соответствующий последнему элементу, должен описывать общее число элементов в множестве (принцип «кардинальности» – использование цифр как количественных числительных).
Чтобы определить, способны ли животные к символизации и удовлетворяет ли их поведение при оценке множеств указанным критериям, необходимо выяснить, могут ли они:
• устанавливать тождество между исходно индифферентными для них знаками (например, арабскими цифрами) и обобщенной информацией о числе элементов множеств разной природы;
• оперировать усвоенными цифрами как символами (например, выполнять операции, аналогичные арифметическим);
• использовать усвоенные символы для нумерации (пересчета) элементов множеств и выполнять число действий в соответствии с предъявленной цифрой.
Оценка способности к «счету» у приматов
Первые исследования способности к символизации были выполнены на человекообразных обезьянах. Японские приматологи под руководством Т. Матцузавы (Институт изучения приматов при университете г. Киото) уже около трех десятилетий исследуют когнитивные способности шимпанзе, включая символизацию и формирование понятия о числе (Matsuzawa 1985; Matsuzawa et al. 1986; Tomonaga, Matsuzawa 2000; Biro, Matsuzawa 2001).
Самку шимпанзе по кличке Аи обучили значениям нескольких десятков иероглифов кандзи (одна из форм японской письменности) для обозначения цвета, числа элементов в множестве и др. Эксперименты проводили с помощью компьютеризованной установки – стимулами служили изображения, появляющиеся на экране чувствительного к прикосновению монитора. Кроме того, без специального обучения Аи усвоила значения трех десятков слов устной речи.
Способность Аи к «счету» исследовали методом выбора по образцу. В качестве образца предъявляли наборы различных предметов, а для выбора – арабские цифры. Аи успешно установила эквивалентность между арабскими цифрами от 1 до 9 и соответствующими множествами. В тесте на перенос с новыми вариантами множеств того же диапазона она выбирала соответствующие им цифры («маркировала» множества с помощью символов – «продуктивное»[35] использование символов). Можно было предположить, что ее обучение ограничивалось образованием условной связи между цифрой и конкретным паттерном расположения элементов в множестве, а также простым запоминанием всех использованных комбинаций. Однако в более поздних работах (Murofushi 1997; Biro, Matsuzawa 2001) было доказано, что дело этим не ограничивается и Аи действительно связала цифры с понятием «число», применяя их к любому множеству данной величины независимо от второстепенных признаков. Она выбирала нужную цифру от 1 до 9 для маркировки разнообразных новых множеств («рецептивное» использование символов), абстрагируясь от паттернов расположения составляющих их элементов, а также от их размера, цвета и формы. Таким образом, эти два эксперимента продемонстрировали способность шимпанзе успешно использовать принцип кардинальности.
Кроме того, Аи усвоила и принцип ординальности: когда ей предъявляли несколько цифр, разбросанных в случайном порядке по экрану монитора, она прикасалась к ним по очереди в порядке возрастания, т. е. как бы в соответствии с имеющимся у нее мысленным упорядоченным рядом (Tomonaga et al. 1993; Tomonaga, Matsuzawa 2000; Biro, Matsuzawa 2001).
Важный вклад в решение вопроса о способности животных к использованию символов для характеристики множеств внесли работы американской исследовательницы Сары Бойзен и ее сотрудников (Boysen, Berntson 1989; 1995; Boysen 1993). Благодаря приемам, специально акцентирующим внимание животного на признаке числа, и постепенному наращиванию сложности предъявляемых задач им удалось обучить шимпанзе Шибу практически всем элементам «истинного счета».
Сначала шимпанзе обучали класть одну и только одну конфету в каждый из шести отсеков специального подноса. Смыслом этой процедуры была демонстрация соответствия «один к одному» между числом отсеков и числом конфет. На следующем этапе в ответ на предъявление подноса с одной, двумя или тремя конфетами шимпанзе должны были выбрать одну из трех карточек с изображениями такого же числа кружков. Авторы особо подчеркивали значение того, что конфеты на поднос помещали по очереди, при этом экспериментатор их вслух пересчитывал. Тем самым обезьяне демонстрировали первый и второй принципы Гельман и Галлистеля – соответствие «один к одному» и упорядоченность (ординальность). Затем карточки с изображениями точек стали постепенно (сначала одну, потом две, а потом и все три) заменять карточками с изображениями цифр, так что обезьяна должна была использовать эти ранее индифферентные для нее изображения вместо изображений реальных множеств.
Когда Шиба стала уверенно выбирать цифру, соответствующую числу конфет на подносе («продуктивное» использование символов), обучение продолжили с помощью компьютера. Обезьяне показывали на мониторе одну из цифр, а она должна была выбрать карточку с изображением соответствующего числа точек (рецептивное использование символов) (рис. 7а, б).
По той же методике Шиба освоила еще два символа: цифры 0 и 4, а впоследствии также 5, 6 и 7. Интересно, что, осваивая новые множества, она сначала по очереди прикасалась к каждой из конфет («пересчитывала» их) и только после этого выбирала соответствующую цифру. Дополнительные опыты свидетельствуют, что это не было простым подражанием действиям экспериментатора, – число ошибочных ответов коррелировало с числом ошибочных касаний пальцем.
Для проверки способности Шибы оперировать усвоенными символами провели следующие два теста. В лаборатории по двум из трех «тайников» раскладывали апельсины таким образом, чтобы их сумма не превышала 4 и их нельзя было видеть одновременно. Шиба обходила все три «тайника» и по очереди видела (но не могла достать) находящиеся в них апельсины. Затем обезьяна должна была подойти к «рабочей площадке», откуда не были видны апельсины, и выбрать из разложенных там цифр ту, которая соответствовала общему числу плодов. Уже во второй серии экспериментов (25 проб в каждой) шимпанзе выбирала правильную цифру более чем в 80 % случаев.
Во втором тесте (его назвали тестом на «счет символов») апельсины заменили карточками с цифрами, которые также помещали в любые два из трех «тайников» (тест на «сложение символов»). Использовали следующие комбинации цифр: 1 и 0, 1 и 1, 1 и 2, 1 и 3, 2 и 0, 2 и 2. Как и на предыдущем этапе, Шиба должна была обойти «тайники» и затем найти карточку с цифрой, соответствующей сумме. В первой же серии она выбрала правильную цифру в достоверном большинстве случаев (75 %). Полученные результаты стали убедительным свидетельством способности шимпанзе усваивать символы, оперировать ими в отрыве от реальных множеств и выполнять операцию, аналогичную сложению, т. е. поведение обезьяны удовлетворяло двум критериям «истинного счета».

Демонстрация способности шимпанзе к использованию принципа ординальности была целью экспериментов Д. Рамбо (Rumbaugh et al. 1989; Rumbaugh, Washburn 1993): животных старались побудить нумеровать объекты с помощью символов или производить определенное число действий в соответствии со значениями цифр. В экспериментах участвовали шимпанзе, ранее обучавшиеся языку-посреднику йеркиш (Лана, Шерман и Остин; см. ниже).
Прежде всего, обезьян научили с помощью джойстика перемещать курсор по экрану монитора и помещать его на арабскую цифру, которая появлялась на соответствующем по счету месте в одной из прямоугольных рамок, расположенных вдоль верхнего края экрана. В следующей задаче вдоль нижнего края экрана дополнительно появлялись изображения прямоугольных рамок с одной точкой внутри каждой. Шимпанзе нужно было передвинуть столько рамок, чтобы их число соответствовало значению арабской цифры-образца. После передвижения последней рамки обезьяна должна была вернуть курсор на цифру-образец, сигнализируя тем самым о выполнении задачи. В процессе обучения, как только обезьяна передвигала очередную рамку нижнего ряда, в верхнем ряду рамок появлялась соответствующая цифра (демонстрация «соответствия один к одному»). В тесте такой «обратной связи» не было. Когда обезьяна помещала курсор на очередную рамку, та исчезала, и при этом раздавался звуковой сигнал. Для успешного выполнения задания было необходимо помнить, сколько рамок уже исчезло. Шимпанзе успешно справлялись с этой задачей. В данной ситуации они продемонстрировали владение обоими принципами – и ординальности, и кардинальности, – и потому их поведение расценили как «начальный счет» (entry-level counting; Rumbaugh, Washburn 1993).
Еще более убедительные доказательства способности животных представлять упорядоченность (ординальность) в ряду чисел были получены даже не на шимпанзе, а на низших обезьянах (Brannon, Terrace 1998).
Опыт проводили следующим образом: на чувствительном к прикосновениям мониторе макакам предъявляли по четыре множества, содержащих от 1 до 4 элементов (рис. 8, см. вклейку). Обезьяны должны были по очереди прикоснуться к каждому из этих множеств в возрастающем порядке. По завершении обучения, когда обезьяны усвоили порядок выбора данных четырех множеств, им предъявляли 150 новых наборов множеств в том же диапазоне от 1 до 4, причем каждый показывали лишь один раз. После того как обезьяны успешно справились с этой задачей, им предъявили множества, содержащие от 1 до 9 элементов. Обезьяны успешно ранжировали новые множества именно по числу элементов в них, используя для этого правило выбора по возрастанию, которому они ранее обучились на множествах, содержащих от 1 до 4 элементов (Brannon, Terrace 1998).
Таким образом, приматы способны распознавать и обобщать признак «число элементов», устанавливать соответствие между этим отвлеченным признаком и ранее нейтральными для них стимулами – арабскими цифрами. Оперируя цифрами как символами, они способны ранжировать множества и упорядочивать их по признаку «число», а также совершать число действий, соответствующее цифре. Наконец, они способны к выполнению операций, изоморфных сложению и вычитанию, но этот вопрос, несомненно, требует более точных исследований.
Способность к символизации у птиц (на примере врановых)
Оценка способности к символизации у животных, не относящихся к приматам, представляет самостоятельный интерес, позволяя судить о том, на каких этапах филогенетического развития появляется эта когнитивная способность. Мы исследовали ее у врановых птиц, и выбор этого объекта был не случаен.
Изучение высших представителей класса птиц (попугаев и врановых) показало, что даже самые высокие степени обобщения – образование довербальных понятий – нельзя считать прерогативой приматов (Зорина и др. 2001; Koehler 1956; Mackintosh 1988; Pepperberg 1999/2002). Развитая функция обобщения и абстрагирования позволяет им оперировать рядом отвлеченных понятий, включая довербальное понятие о «числе» (Зорина, Смирнова 1995; Смирнова и др. 1998, 2002; Smirnova et al. 2000; Pepperberg 1991, 1996; Pepperberg, Gordon 2005). Поэтому появилось основание проверить, способны ли вороны к символизации, т. е. могут ли они установить эквивалентность цифр от 1 до 4 и соответствующих им множеств. Для этого был разработан особый методический подход (Зорина и др. 2001). В отличие от предыдущих исследований (Matsuzawa et al. 1986; Matsuzawa 1985; Murofushi 1997), у ворон не вырабатывали ассоциативных связей «цифра и соответствующее ей множество», но создавали условия для того, чтобы птицы смогли самостоятельно выявить эту связь на основе информации, полученной в специальных «демонстрационных» сериях.
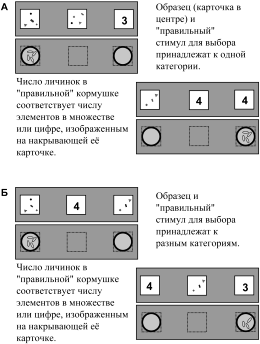
В «демонстрационной» серии впервые за весь период обучения птицы одновременно видели и цифры и множества – например, если образцом была цифра 4, то для выбора предъявляли какое-нибудь множество и цифру 4, а если образцом было множество из четырех элементов, то на карточках для выбора изображали какую-нибудь цифру и множество из четырех элементов (рис. 9А). Кроме того, вороны получали информацию о «цене» каждого стимула. В случае правильного выбора они получали дифференцированное подкрепление: находили то число личинок, которое соответствовало цифре или множеству на выбранной ими карточке. Например, и под карточкой с множеством из четырех элементов, и под цифрой 4 ворона находила 4 личинки. Для успешного решения задачи в демонстрационных сериях воронам достаточно было использовать ранее усвоенное правило выбора по соответствию с образцом – «выбирай изображение, похожее на образец».
В тесте мы выясняли, могут ли птицы установить эквивалентность цифр и соответствующих им множеств без направленного формирования такой связи. В этом опыте образец впервые принадлежал к одной категории, а обе карточки для выбора – к другой (рис. 9Б). Например, если образцом была цифра 4, то для выбора предъявляли два множества, но только одно из них состояло из четырех элементов. Если образцом было множество из четырех элементов, то для выбора предъявляли две цифры, одна из которых была четверкой. Таким образом, между образцом и карточками для выбора не было внешнего соответствия. Для успешного решения такой задачи воронам нужно было не только использовать ранее усвоенное правило выбора по образцу, но и произвести дополнительные операции, мысленно сопоставить еще какую-то ранее полученную информацию об образце и стимулах для выбора. Такой информацией было число единиц подкрепления, связанное с каждым из стимулов во время демонстрационных серий,
Птицы с первых же проб решали эту задачу правильно: в достоверном большинстве случаев они выбирали цифру, соответствующую изображенному на образце множеству и наоборот. Следовательно, вороны способны без специального обучения, за счет мысленного сопоставления ранее полученной информации, установить эквивалентность множеств и исходно индифферентных для них знаков (цифр от 1 до 4).
Мы предполагаем, что в данном случае птица принимала решение с помощью операции логического вывода, которую называют транзитивным заключением (см. ниже, раздел «Операции логического вывода»). Поскольку ранее каждому графическому множеству и каждой цифре соответствовало определенное число личинок, то выбирать нужно тот стимул, за который ранее давали столько же личинок, сколько и за образец (если А = В и В = С, то А = С). То есть, на основе двух посылок, полученных ассоциативным или условно-рефлекторным путем, животное может сделать вывод о наличии третьей связи.
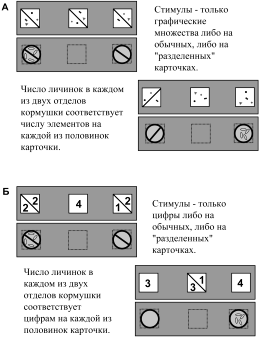
В следующем эксперименте мы выясняли, могут ли птицы оперировать усвоенной информацией – выполнять с цифрами комбинаторную операцию, аналогичную арифметическому сложению. «Слагаемые» (цифры или множества) были изображены на карточках, разделенных по диагонали чертой, так же как и соответствующие им кормушки были разделены вертикальной перегородкой на две равные части (рис. 10А). В «демонстрационной» серии использовали только множества либо на обычных, либо на «разделенных» карточках и демонстрировали соответствие числа элементов на обычных либо на «разделенных» карточках числу личинок в обычных или в «разделенных» кормушках.
В отличие от «демонстрационной» серии, в тесте на «сложение» мы использовали только цифры. Если в качестве образца предъявляли отдельную цифру, то для выбора – две «разделенные» карточки с цифрой в каждой половине, сумма которых на одной из них соответствовала цифре на образце (рис. 10Б). Если в качестве образца использовали «разделенную» карточку с парой цифр, то для выбора предлагали отдельные цифры.
Птицы успешно справились с этой задачей. К началу серии они уже знали, что каждому конкретному графическому множеству и каждой цифре соответствует определенное число личинок, и на этом основании во время теста они (экстренно) определяли, что определенные цифры и графические множества соответствуют друг другу. Затем, в ходе демонстрационной серии вороны получали дополнительную информацию о том, что под карточкой с «разделенным» множеством находится соответствующим образом «разделенное» число личинок. Для правильного выполнения теста на «сложение» им нужно было сделать мысленное заключение об эквивалентности друг другу отдельных цифр и соответствующих комбинаций двух цифр.
Оказалось, что вороны способны сохранять информацию о числовых признаках стимулов не только в форме образных представлений, но и в некой отвлеченной и обобщенной форме, которую они смогли связать с ранее нейтральными для них знаками – цифрами. Следовательно, не только у высших приматов, но и у некоторых птиц довербальное мышление достигло в своем развитии того промежуточного этапа, который, по мнению Орбели (1949), обеспечивает возможность использования символов вместо реальных объектов и явлений и который в эволюции предшествовал формированию второй сигнальной системы.
Основываясь на результатах целого ряда поведенческих тестов, Л. В. Крушинский (1986) высказал предположение о существовании параллелизма в эволюции высших когнитивных функций птиц и млекопитающих – позвоночных с разными типами структурно-функциональной организации мозга. Мы привели эти данные, чтобы показать, что обобщение, абстрагирование, формирование довербальных понятий и способность к символизации – достаточно универсальные когнитивные операции, в сходной степени присущие высшим представителям разных классов позвоночных.
С тех пор всё новые и новые данные подтверждают, что, несмотря на принадлежность к различным ветвям эволюции и кардинальные различия в структуре мозга, способность к разным видам элементарного мышления, в том числе к обобщению и абстрагированию, у представителей этих классов характеризуется сходными градациями. Это свидетельствует о том, что предыстория человеческого мышления восходит к достаточно древним этапам филогенеза, общим для предков этих классов.
Операции логического вывода
Говоря о мышлении животных в контексте обучения обезьян языкам-посредникам, нельзя не упомянуть о способности животных к совершению двух операций логического вывода (inferential reasoning), когда при получении новой информации ее усвоение происходит на основе уже имеющейся, путем мысленного сопоставления ранее полученных сведений. Об этих операциях необходимо упомянуть по двум причинам. Во-первых, само начало их изучения связано с именем Д. Примэка – одного из первопроходцев в области изучения зачатков речи у обезьян (Gillan et al. 1981; Premack 1983; Premack & Premack 1972, 2003). Во-вторых, одна из операций – транзитивное заключение – тесно связана с процессом символизации.
Транзитивное заключение
Упомянутое выше транзитивное заключение составляет одну из базовых операций, присущих дедуктивному мышлению человека. Определение транзитивного отношения пришло в психологию из формальной и математической логики. Отношение r называют транзитивным, если оно, попарно связывая стимулы B и C, C и D, с необходимостью связывает также стимулы B и D. Стимулы, связанные такими отношениями, образуют транзитивный ряд: B r C r D. Таким образом, если субъект способен из двух предпосылок B r C и C r D сделать вывод, что B r D, то говорят, что он способен к транзитивному заключению. Примерами транзитивных отношений могут служить такие, как «больше, чем» (например, если B > C и C > D, то B > D), «дальше», «ярче» и т. д. Наряду с отношением транзитивных неравенств существует и возможность транзитивного равенства: если A=B и B=C, то A=С. Именно эта операция, как мы увидим, вовлечена в процесс символизации у птиц – в превращение нейтральных для них стимулов (цифр) в символы-числительные, которыми они далее оперируют вместо соответствующих множеств.

