Оценка компаний: Анализ и прогнозирование с использованием отчетности по МСФО

• МСФО шире использует справедливую стоимость. В частности, в соответствии с МСФО объекты недвижимости как в фондах недвижимости, так и в других компаниях могут отражаться по справедливой стоимости, а в US GAAP нет.

Напомним, что FASB и IASB решили устранить все значительные расхождения между двумя стандартами финансовой отчетности в ближайшее время. Поэтому мы увидим их постепенное сближение.

Глава 1

Про денежные потоки и финансовую отчетность

1. Принципы оценки

Прежде чем рассматривать методы оценки, которые мы используем, напомним основы оценки стоимости акционерного капитала.

Язык оценки – финансовые коэффициенты

Откройте финансовый раздел любой газеты, и вы увидите в таблице курсов акций по меньшей мере два коэффициента: цена / прибыль (P/Е) и дивидендная доходность. Коэффициент P/Е определяется как отношение рыночной стоимости акций к чистой прибыли компании, полученной за предыдущий год. Дивидендная доходность – это сумма дивидендов, выплаченных компанией за последние двенадцать месяцев, деленная на рыночную стоимость акций. Первый коэффициент показывает срок окупаемости вложений в акции: сколько лет потребуется, чтобы вернуть вложенные деньги? Второй коэффициент показывает, сколько будет получено на единицу вложенных средств.

Существует третий важный коэффициент. Его приводят реже, хотя теоретические исследования показывают, что он позволяет точнее прогнозировать колебания курсов акций. Это коэффициент цена / балансовая стоимость (Price-to-Book Ratio, P/B), определяемый как отношение рыночной цены к балансовой стоимости акции. Он показывает размер премии, уплачиваемой сверх суммы, инвестированной в бизнес (оплаченного акционерного капитала и нераспределенной прибыли).

Три коэффициента взаимосвязаны. Реинвестируя прибыль, вместо того чтобы выплачивать ее в виде дивидендов, компании увеличивают балансовую стоимость акционерного капитала. При этом, выбирая между акциями с высоким коэффициентом P/E, акциями с низкой дивидендной доходностью или акциями с высоким коэффициентом P/B, инвестор исходит из одинаковых предположений. Инвестор всегда будет платить больше за акции компании, которая выглядит более надежной, более прибыльна и растет быстрее других.

Показатели доходности: IRR и NPV

Когда компании принимают инвестиционные решения, они не ограничиваются простыми расчетами периода окупаемости. Более сложные подходы предусматривают расчет внутренней нормы доходности инвестиций (IRR) или использование требуемой нормы доходности в качестве ставки дисконтирования для вычисления приведенной стоимости (PV), из которой путем вычитания первоначальных инвестиционных затрат получают чистую приведенную стоимость (NPV). Если NPV имеет положительное значение – инвестировать целесообразно; если нет – инвестировать нецелесообразно.

Аналогичный подход применяют к оценке акций. Можно пойти дальше простых мультипликаторов для определения приведенной стоимости, и значительная часть этой книги посвящена интерпретации финансовой отчетности и построению моделей, которые определяют приведенную стоимость более точно. Но не следует забывать: точно так, как существует взаимосвязь между периодом окупаемости и IRR (быстрой окупаемости обычно соответствует высокое значение IRR), как правило, существует связь и между простыми коэффициентами, в которые входит цена акции, при условии, что они поддаются разумной интерпретации и являются результатами более сложной модели оценки акции.

Модели оценки стоимости: сложность против простоты

В самых простых случаях (когда денежный поток стабилен или бесконечно растет с постоянной скоростью) расчеты с использованием сложной модели оценки стоимости и применение простого коэффициента дадут одинаковый результат. Применение сложных моделей оправдано только тогда, когда темп роста денежных потоков непостоянный. Это справедливо при оценке как компаний, так и отдельных инвестиционных проектов.

Оценка стоимости всей компании, а не акционерного капитала

При оценке акций используется два основных подхода: 1) непосредственная оценка акционерного капитала; 2) сначала оценка бизнеса в целом (долг плюс собственный капитал), а потом вычитание долговых обязательств. Главное преимущество второго способа: он позволяет разделить вопросы оценки стоимости компании и ее финансирования и использовать более понятные показатели финансовой отчетности. Указанные выше коэффициенты (P/E, P/B и дивидендная доходность) относятся исключительно к акционерному капиталу, но аналогичные коэффициенты существуют и для оценки бизнеса – например, стоимость компании к инвестированному капиталу (EV/invested capital) или стоимость компании к чистой операционной прибыли после уплаты налогов (EV/NOPAT). Подход через оценку бизнеса в целом часто более понятен, чем непосредственная оценка акционерного капитала. Например, если вы оцениваете свой дом, разумнее опираться на рентный доход, который он мог бы приносить, вычитая затем затраты на ипотечный кредит, нежели мыслить в терминах денежных потоков за вычетом уплачиваемых процентов. На практике никто не станет применять последний подход, оценивая дом, – почему же следует поступать иначе при оценке компании?

Проблемы использования денежного потока

И последнее. Читатели могли слышать о другой группе коэффициентов. Они не имеют отношения ни к балансовой стоимости, ни к прибыли, ни к доходам – только к денежным потокам от основной деятельности. Одна из задач этой книги состоит в том, чтобы побудить читателей использовать подобные показатели (денежная прибыль на акцию, EBITDA к стоимости бизнеса) максимально осторожно. Во-первых, они редко дают точное представление о реальных денежных потоках. Во-вторых, даже если при помощи этих коэффициентов можно получить реальные денежные потоки, они не дают представления об устойчивом потоке, поскольку предшествуют инвестициям, необходимым для дальнейшего существования компании. Если их использовать без поправок, они могут помочь только в определении ликвидационной стоимости, а не стоимости действующего предприятия.

Связь между мультипликаторами и приведенной стоимостью

Многое из сказанного выше, как мы надеемся, станет понятнее к концу главы. На первый взгляд формулы, которые мы будем использовать, могут показаться непохожими на знакомые коэффициенты Р/Е или показатели доходности в финансовых изданиях. Но мы надеемся, что к концу главы читатели изменят свое мнение и убедятся, что на самом деле сходство достаточно велико и существуют серьезные основания использовать более сложные подходы.

Все математические расчеты мы перенесли в отдельное приложение (см. Аналитические формулы). Те, кому интересно, смогут найти в приложениях необходимые параметры моделей оценки, но это не главная цель настоящей книги. По опыту авторов, большинство практиков постоянно пользуются идеями этой главы, и лишь немногие могут объяснить, как они работают! Наша цель: снабдить всех читателей средствами для моделирования деятельности и оценки стоимости компаний, а всем, кто интересуется, предоставить теоретическое обоснование.

2. Распределение прибыли, доходов и рост

Многие книги по оценке пишутся с целью доказать преимущества одних формул или механически применяемых действий по сравнению с другими. Сторонники моделей дисконтированных денежных потоков (DCF), экономической добавленной стоимости (EVATM), денежной доходности инвестиций (CFROI), дисконтирования дивидендов и остаточного дохода готовы вступить в бой за превосходство своего метода. Мы подробнее остановимся на каждом из методов, но основная наша цель не в этом. Мы расскажем о подходах, по нашему мнению, более предпочтительных для оценки компаний определенного вида. Но об одном принципиальном моменте следует сказать с самого начала: при правильном применении все основные методы оценки должны давать одинаковые результаты для одной компании. Результат не должен зависеть от того, рассматривается денежный поток или экономическая прибыль, или денежный поток соотносится с инвестированным или акционерным капиталом компании.

Механизм получения оценки компании на основе прогнозов очень важен. Но важнее знать, как строятся прогнозы, как историческая финансовая отчетность согласуется с прогнозами. Такие взаимосвязи, по нашему убеждению, часто игнорируются или понимаются неверно.

Для начала несколько упростим картину. Возьмем компанию, на балансе которой нет долговых обязательств. Каждый год она (как мы надеемся) получает некоторую прибыль. Размер прибыли определяется после вычитания денежных затрат (себестоимость реализованной продукции, заработная плата, налоговые выплаты и прочие расходы) и отчислений (резервов) на возмещение износа основных средств. Эти резервы известны как амортизация. Таким образом, в нашем очень простом примере входящий денежный поток компании равен сумме чистой прибыли и амортизации. Исходящий поток составляют: капитальные затраты, увеличение оборотного капитала (материальные запасы и счета к получению за вычетом счетов к оплате), а также дивиденды, распределяемые среди акционеров.

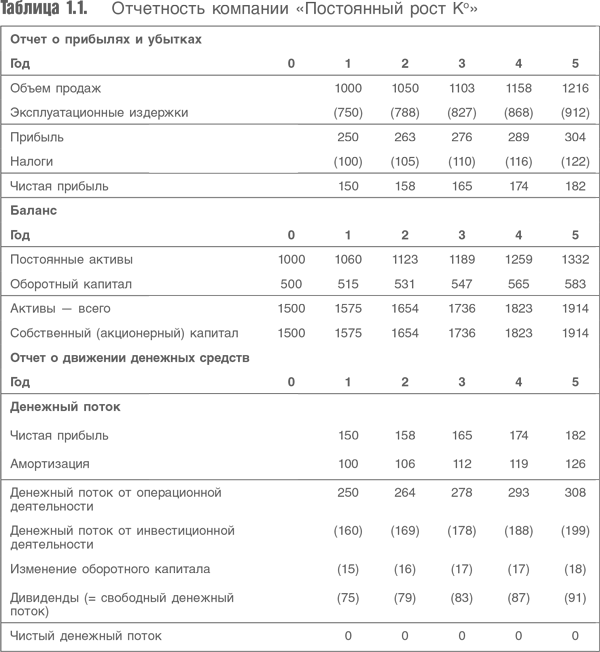
Предположим, что у компании не будет долгов и денежных средств на балансе. Таким образом, объем дивидендов каждый год должен равняться денежному потоку за вычетом капитальных затрат и изменения оборотного капитала (свободный денежный поток). В табл. 1.1 приведены отчет о прибылях и убытках, бухгалтерский баланс и отчет о движении денежных средств компании «Постоянный рост К°».

Теперь представим, что мы знаем ставку дисконтирования для потока дивидендов (свободного денежного потока), которые ожидаем получить от компании. Чтобы преобразовать все будущие денежные потоки в текущие значения, мы можем использовать стандартную формулу дисконтирования:

PV = CFt / (1+k)t,

где PV – текущая стоимость денежного потока в году t (CFt), дисконтированного по ставке, равной стоимости акционерного капитала (k).

Заранее не известно, когда может прекратиться деятельность компании. Поэтому в отличие от того, как поступают с облигациями, мы дисконтируем денежный поток, продолжающийся до бесконечности. Это одна из проблем, возникающих при оценке акций. Другая состоит в том, что даже среднесрочные изменения денежных потоков сложно предвидеть. Таким образом, если мы не хотим прибегать к использованию бесконечно длинных таблиц, в какой-то момент нужно остановиться и предположить, что начиная с этой точки темп роста компании будет постоянным. Он может быть отрицательным, нулевым или положительным, но обычно принимается положительным.

Как можно рассчитать текущую стоимость потока, который будет расти бесконечно (рис. 1.1)?

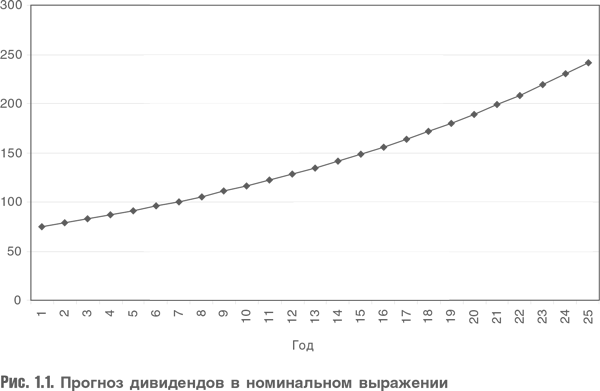
Проблема заключается в том, что каждый прогнозируемый показатель больше предшествующего. Но решение есть. Если ставка дисконтирования больше темпа роста, то дисконтированный поток дивидендов к текущим (приведенным) значениям будет уменьшаться (рис. 1.2).

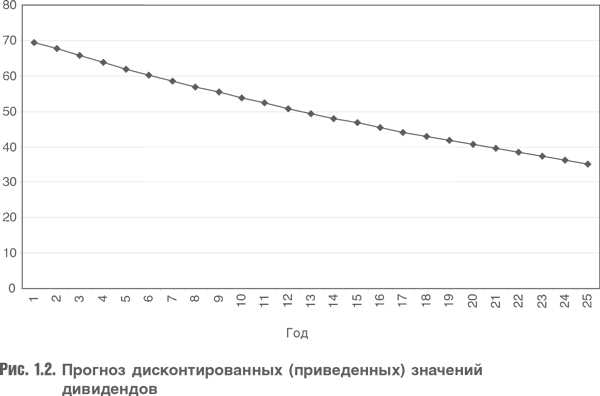
Приведенные значения уменьшаются, поэтому они меньше влияют на результат. Существует простая формула определения величины, к которой стремится сумма текущих значений, когда поток дивидендов не ограничен во времени. Она известна как модель роста Гордона и записывается следующим образом:

V = D × (1 + g)/(k – g),

где V – текущая стоимость, D – величина дивидендов последнего года, g – темп роста и k – ставка дисконтирования. Очевидно, данная модель дает разумный результат, если ставка дисконтирования превышает темп роста (k>g). (Доказательство модели Гордона дано в приложении.) Поскольку модель Гордона является общей формулой для оценки бесконечных потоков с постоянным темпом роста, она применима в равной степени для оценки как потока дивидендов, так и генерируемого денежного потока.

Это все, что нам требуется для оценки компании. Мы прогнозируем наши финансовые показатели на несколько лет вперед, принимаем как предпосылку постоянный темп роста, затем конвертируем поток дивидендов после последнего прогнозируемого года в так называемую терминальную (конечную) стоимость. Если мы сложим текущую стоимость дивидендных выплат в прогнозируемом периоде и дисконтированную величину конечной стоимости (поскольку эта стоимость относится к концу прогнозного периода и мы должны привести ее к текущему моменту), то получим сегодняшнюю оценку акционерного капитала компании.

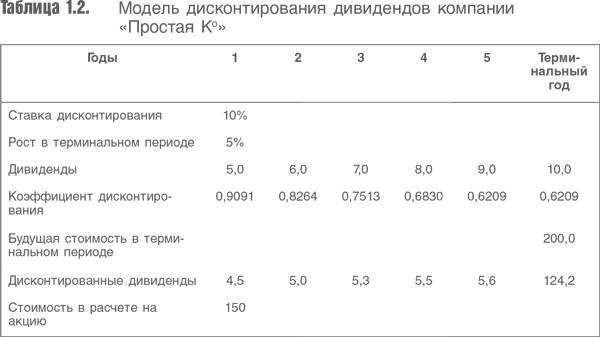
В табл. 1.2 приведена оценка компании «Простая К°», которая выплачивает дивиденды, возрастающие за следующие пять лет с 5 до 9 (очевидно, этот рост не соответствует постоянной ставке, выраженной в сложных процентах), а затем растущие на 5 % в год с базового уровня 10 в шестом году. Поскольку год 6 используется в качестве базы для оценки всех дивидендов, выплачиваемых в этом и всех последующих годах, его часто называют «терминальным» годом. Если мы применяем модель Гордона (модель роста), то при ставке дисконтирования 10 будущая оценка конечной стоимости составит 200. Это означает, что стоимость акционерного капитала компании «Простая К°» через пять лет будет составлять 200. Однако нас интересует текущая оценка. Поэтому нам потребуется пять множителей дисконтирования дивидендов отдельных лет и конечной стоимости. Стандартная формула дисконтирования стоимости выглядит так:

PV = FV / (1+k)n,

где PV – приведенная стоимость, FV – будущая стоимость, k – ставка дисконтирования, n – количество лет.

Заметьте, что конечная стоимость дисконтируется на пять, а не на шесть лет, хотя она основана на величине дивиденда года 6. Это объясняется тем, что в модели Гордона в качестве первого члена используется величина, которая ожидается спустя год. Таким образом, денежный поток, который начинается на году 6, учитывается как величина, относящаяся к году 5, затем мы должны привести ее к текущей стоимости путем дисконтирования на пять лет.

К сожалению, в подавляющем большинстве моделей оценки, применяемых в банках, инвестиционных и производственных компаниях, этим и ограничиваются. Конечно, эти модели корректируются, поскольку компании могут финансироваться путем заимствований или увеличения акционерного капитала (к этому вопросу мы еще вернемся), включать в свою отчетность нематериальные активы, запасы и другие элементы (часто неудачно – этот вопрос мы рассмотрим позже). Но в принципе, большинство работают именно так, и в этой простоте кроется опасность.

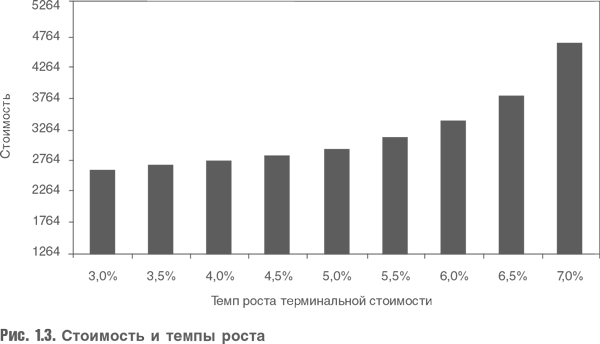
Вернемся к компании «Постоянный рост К°» и изменим темп роста, учитываемый при расчете терминальной стоимости (рис. 1.3).

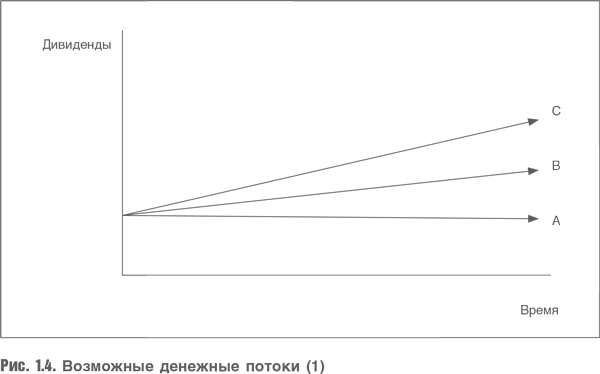
Минимальное изменение темпа роста резко меняет оценку стоимости, часть стоимости в размере 1264 составит сумма дивидендов за 25 лет прогнозного периода, поэтому столбцы отражают изменение стоимости за счет темпов роста в постпрогнозном периоде. Но разве это возможно? Чтобы ответить на этот вопрос, рассмотрим компоненты модели Гордона: дивиденды, темп роста и ставка дисконтирования. На самом деле мы меняем темп роста, оставляя другие компоненты неизменными. Насколько это оправданно? Может ли темп роста компании изменяться, но при этом компания распределяет один и тот же объем дивидендов? Конечно, нет. Если мы хотим расти быстрее, то должны реинвестировать большую часть прибыли в расширение бизнеса. Другая крайность: выплатить всю прибыль в виде дивидендов, при этом темп роста будет нулевым. В нашем первом расчете мы предполагали, что варианты выглядят примерно так, как на рис. 1.4. В наших вычислениях мы предполагали, что темп роста компании изменяется, а объем реинвестированной прибыли остается неизменным, что выглядит довольно странно.

Но реальность такова: если компания хочет расти быстрее, она должна реинвестировать бóльшую часть своей прибыли. И если она выплачивает бόльшую часть прибыли в виде дивидендов, то это неизбежно приведет к более низким темпам роста. Поэтому реальная картина выглядит так, как показано на рис. 1.5.

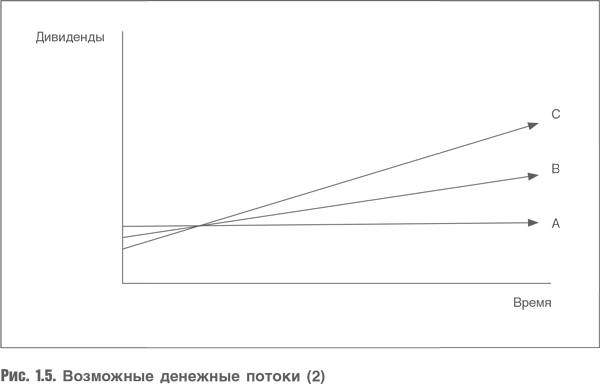
Возникает выбор. Либо распределяем бóльшую долю прибыли в виде дивидендов, но при этом темп роста будет более низким, либо получаем меньше от компании сегодня с целью больше реинвестировать, при этом ожидая более высоких темпов роста доходов в будущем. От чего зависит выбор? От доходности, которую мы получим на дополнительный инвестированный капитал. Данную взаимосвязь выражает формула (доказательство см. в Приложении):

g = b × R,

где g – темп роста, b – доля реинвестируемой прибыли, R – доходность вновь привлекаемого акционерного капитала.

Заметьте, что доходность вновь привлекаемого акционерного капитала не обязательно должна совпадать с доходностью существующего акционерного капитала. Предположим, мы имеем бизнес, дающий фантастические доходы – например, идеально расположенные фешенебельные магазины. Может случиться так, что они будут продолжать приносить высокие доходы без увеличения инвестиций. Но если мы решаем инвестировать часть прибыли в новые объекты (возможно, менее привлекательные), то доходность вновь привлекаемого акционерного капитала будет ниже, чем доходность старого. Это доходность дополнительного капитала, который генерирует дополнительную прибыль.

Обычно мы размышляем об этом, подходя к вопросу с другой стороны. Вместо того чтобы устанавливать долю нераспределенной прибыли, иногда разумнее устанавливать темп роста и доходность, а по ним определять долю нераспределенной прибыли. Тогда:

b= g/R.

Доля распределенной прибыли как часть денежного потока, который мы будем дисконтировать, равна (1 – b). Таким образом, размер дивидендов в произвольный год будет равен:

D = Y × (1 – g/R),

где Y – прибыль.

Включив это в модель Гордона, получим:

V = Y × (1 – g/R) / (k – g),

где Y – прибыль, R – доходность вновь привлекаемого акционерного капитала, k – ставка дисконтирования и g – темп роста.

Теперь мы имеем формулу, которая позволяет нам оценивать денежные потоки. Они более приближены к реальному примеру, приведенному на рис. 1.5. Возникает важный вопрос: как изменится оценка, если предположить, что компания может выбирать разные размеры реинвестирования и, соответственно, разные темпы роста?

Рассмотрим пример. В табл. 1.3 показана оценка стоимости в расчете на акцию для базового случая и влияние темпа роста и доходности дополнительного капитала на стоимость. В качестве базового случая примем: доходность в расчете на акцию – 10 %, темп роста – 5 % и ставка дисконтирования – 8 %.

Сначала рассмотрим предельные значения. Если компания распределяет всю прибыль и не растет, то понятие «доходность дополнительного капитала» неприменимо, так как он отсутствует. В этом случае стоимость компании определяется как объем прибыли деленный на ставку дисконтирования. Теперь предположим, что доходность дополнительных инвестиций компании равна ставке, по которой рынок их дисконтирует. Очевидно, что размер дополнительных инвестиций не повлияет на стоимость и не будет зависеть от предположений о темпе роста. Новые инвестиции и обусловленный ими рост имеют значение только в том случае, если получаемая компанией доходность либо превышает стоимость собственного капитала, либо меньше ее. Рост может навредить. Посмотрите, что случится, если мы увеличим темп роста при R

Существуют реальные примеры компаний, цены акций которых упали до уровня, до которого они бы никогда не упали, если бы менеджмент компании пообещал не инвестировать дополнительные средства в компанию. Обычно в итоге такие компании подвергаются поглощению. В наше время, когда растет активность акционеров, возможной альтернативой могло быть смещение такого менеджмента группой институциональных акционеров.

Вернемся к началу главы, чтобы обсудить прочитанное. Разумеется, примеры носят очень упрощенный характер. Мы рассматриваем компании, темп роста которых постоянный, доходность дополнительных инвестиций стабильная, отсутствуют заимствования. В последующих главах эти предположения будут опущены. Но из изложенного выше ясно, что невозможно оценивать компанию, не принимая во внимание ее доходность.

Задумайтесь еще раз над нашим простейшим примером экстраполяции (рис. 1.4). Зная результат, мы можем догадаться, что должно существовать неявное предположение об уровне доходности на акцию для определенного темпа роста. Если компания может расти быстрее, выплачивая те же дивиденды и реинвестируя ту же сумму капитала, она должна добиваться более высокой доходности этого дополнительного акционерного капитала. В качестве упражнения посмотрите на табл. 1.4. И спросите себя, инвестируется слишком много или слишком мало, чтобы темп роста составил предполагаемые 5 %?

Эта компания имеет прибыль 100. Она реинвестирует ежегодно 20 % своей прибыли, темп роста составляет 5 % в год. Таким образом, доходность вновь привлекаемого акционерного капитала должна составить 25 %! И чем больше предполагаемый рост, тем выше должна быть предполагаемая доходность. Не удивительно, что на рис. 1.3 показаны столь впечатляющие результаты при увеличении предполагаемых темпов роста.

В результате невозможно построить модель денежных потоков, не зная предположений об ожидаемом размере прибыли. Неявные предположения опасны. Лучше делать их явными. Но откуда в реальной жизни они могут взяться? Ясно, что на них будет оказывать сильное влияние прошлый опыт компании, а также опыт ее конкурентов, представленный в их финансовой отчетности. А это, в свою очередь, означает, что цифры, зафиксированные в финансовой отчетности компаний, имеют очень большое значение.

Приняв еретическое утверждение, что предпосылки в модели дисконтированного денежного потока зависят от финансовой отчетности, сделаем еще один шаг вперед. Мы покажем, что в процессе оценки должны учитываться показатели, которые не отражают денежных потоков, и не должны учитываться показатели измеримого входящего денежного потока компании. Подобные рассуждения могут показаться слишком сложными, но мы попробуем их прояснить.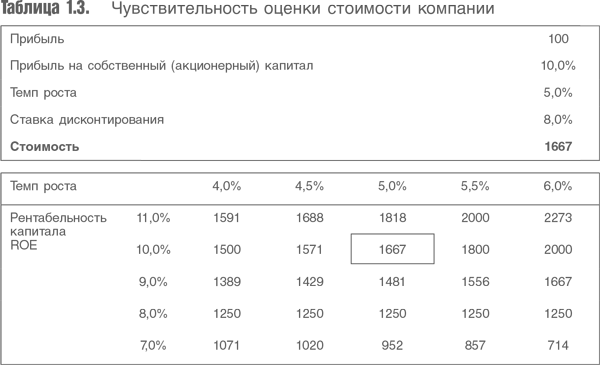

3. Денежные статьи баланса, начисления и прибыль

Представьте себе компанию – владельца недвижимости, которая ежегодно имеет доход от аренды в размере 5 % от рыночной стоимости своей собственности. Кроме того, рыночная стоимость имеющейся собственности компании растет на 5 % в год. Ее административные и финансовые затраты также составляют ежегодно 5 % рыночной стоимости ее портфеля.

Это достаточно простая компания. У нее нулевой денежный поток до новых инвестиций в новые объекты собственности, но если компания начинает расширяться, ее денежный поток оказывается отрицательным. Ее стоимость растет каждый год в результате новых инвестиций и 5 %-ного роста стоимости первоначального портфеля.

Теперь представим, что мы рассчитываем дисконтированный денежный поток нашей компании. Пока она росла, то должна была иметь отрицательный денежный поток. При прекращении роста денежный поток окажется нулевым. Но стоимость портфеля компании при этом продолжала бы расти на 5 % в год без новых инвестиций. В любой момент можно было бы обратить эти начисления в наличность – просто надо ликвидировать портфель и реализовать ценности. Мы хотим разработать метод оценки, который отражал бы, что компания добавила 5 % к стоимости своих первоначальных активов, но не учитывал этот факт в ее денежном потоке.

Мы выявляем две формы прироста стоимости нашей компании. Первая – реальный денежный поток, создаваемый рентными платежами. Вторая – увеличение стоимости объектов собственности без их реализации. Им противопоставляются управленческие и финансовые затраты.

Рассмотрим другой пример. Предположим, что мы анализируем энергетическую компанию, все предприятия которой – атомные электростанции. Можно ожидать, что они почти постоянно будут генерировать существенные денежные потоки, поскольку текущие затраты атомной электростанции малы. Однако расходы на предстоящий вывод станции из эксплуатации достаточно велики. Поэтому данная генерирующая компания может отражать в финансовой отчетности прибыль за вычетом значительных резервов на возможную консервацию атомной станции.

Здесь ситуация, противоположная первому случаю. Дисконтирование растущих бесконечно совокупных денежных потоков на основе отчетности этой компании даст неправдоподобно высокую ее оценку, поскольку при этом неявно предполагается, что ее атомные станции будут существовать вечно. Можно ли решить проблему, принимая резервы, включенные в бухгалтерский баланс и вычитая их из нашей оценки, как если бы они были заимствованиями? Нет, поскольку так можно поступать только с затратами, которые связаны с ликвидацией этого поколения атомных станций. А как быть с генераторами нового поколения? Помимо всего прочего, мы экстраполируем объем продаж в бесконечность, но тогда мы должны экстраполировать в бесконечность и эти огромные, крайне нерегулярные затраты.