Красота физики. Постигая устройство природы

1. Мы, люди, в первую очередь визуальные существа. Конечно, наше зрение и наши самые глубинные виды мышления (множеством менее очевидных способов) обусловлены нашим взаимодействием со светом. Каждый из нас, например, рожден, чтобы в совершенстве, хотя и неосознанно, практиковать проективную геометрию. Эта способность жестко вмонтирована в наш мозг. Именно это позволяет нам интерпретировать двумерное изображение, которое получает наша сетчатка, как представление о мире объектов в трехмерном пространстве.

Наш мозг содержит специализированные модули, которые позволяют нам быстро и без сознательных усилий создавать динамическое представление о мире, в основе которого – трехмерные объекты, расположенные в трехмерном пространстве. Мы делаем это, начиная с двумерных изображений на нашей сетчатке глаз (которые, в свою очередь, образуются благодаря лучам света, испущенным или отраженным от поверхностей внешних предметов, которые распространяются до нас по прямой). Восстановить из полученных нами изображений предметы, которые были их причиной, – непростая задача в инверсной проективной геометрии. На самом деле утверждается, что это неразрешимая задача, потому что в проекциях совершенно недостаточно информации, чтобы сделать однозначную реконструкцию. Основная проблема в том, что, даже чтобы просто начать ее решать, нам нужно отделить объекты от их фона (или от того, что находится перед ними). Чтобы достичь этого, мы пользуемся всевозможными уловками, основанными на типичных свойствах объектов, которые нам встречаются, таких как их цвет или контрастность текстуры и отчетливые границы. Но даже после того, как эта стадия успешно пройдена, нам остается сложная геометрическая задача, для которой Природа любезно снабдила нас превосходным специализированным процессором в нашей зрительной коре[3].

Другая важная черта нашего зрения состоит в том, что свет приходит к нам очень издалека и дает нам возможность заниматься астрономией. Видимое регулярное движение звезд и чуть менее систематическое движение планет послужили ранними намеками на подчинение Вселенной определенным законам и предоставили нам изначальное вдохновение и поле для проверки математического описания Природы. Как любой хороший учебник, оно содержит задачи различной степени сложности.

В самых передовых, современных разделах физики мы узнаем, что свет сам является формой материи, а также то, что на самом деле и материя в целом, при глубоком ее понимании, необыкновенно похожа на свет. Итак, еще раз: наш интерес и опыт соприкосновения со светом, который глубоко заложен в самой нашей природе, оказываются удачными и способствующими познанию.

Существам, которые, как большинство млекопитающих, воспринимают мир прежде всего через обоняние, было бы гораздо сложнее добраться до той физики, которую мы знаем, даже если бы они обладали высоким интеллектом в других областях. Можно вообразить, например, собак, эволюционирующих в очень умных социальных существ, с развитым языком, живущих интересной полной жизнью, но лишенных отдельных видов любопытства и мироощущения, которые основаны на зрительном опыте и которые ведут к нашему виду глубокого понимания физического мира. Их мир был бы полон синтезов и разложений – у них были бы прекрасные наборы для химии, сложная кухня, афродизиаки и, как у Пруста, непроизвольная память. Проективная геометрия и астрономия, возможно, не были бы так представлены. Мы знаем, что запах – это химическое чувство, и мы начинаем понимать его основы в виде молекулярных событий. Но «обратная» задача понять по запаху, какие молекулы вызвали его и какие законы им свойственны, и в конце концов прийти к физике, какой мы ее знаем, кажется мне безнадежно сложной.

Птицы же – визуальные существа, как и мы. Кроме того, их образ жизни дал бы им дополнительное преимущество перед людьми в том, чтобы начать понимать физику. Птицы с их свободой полета испытывают присущую трехмерному пространству симметрию столь хорошо знакомым им способом, которого у нас нет. Они также испытывают основные законы движения (и особенно роль инерции в своей повседневной жизни), так как они существуют в практически лишенной трения среде. Птицы рождаются, можно сказать, с интуитивным знанием классической механики и принципа относительности Галилея, так же как и геометрии. Если бы какие-нибудь виды птиц развили хорошее абстрактное мышление, т. е. перестали бы иметь «птичьи мозги», они бы быстро создали физику. А вот людям пришлось отучиваться от нагруженной трением аристотелевой механики, чтобы достичь более глубокого понимания. Исторически для этого потребовались немалые усилия!

Дельфины в их водной среде и летучие мыши с их эхолокацией предоставляют нам другие вариации на эту тему, но я не буду развивать их здесь.

Основной философский аргумент, который эти соображения иллюстрируют, состоит в том, что мир не дает своей собственной уникальной интерпретации. Мир предлагает множество возможностей для разных вселенных, основанных на разных чувствах, которые способствуют совершенно разным интерпретациям значимости мира. В этом смысле наша так называемая Вселенная уже очень похожа на мультивселенную.

2. Успешное восприятие включает в себя сложные умозаключения, поскольку информация, которую мы получаем о мире, одновременно очень неполная и сильно «зашумлена» побочными сигналами. Несмотря на наши врожденные способности, мы также должны учиться видеть, взаимодействуя с миром, формируя ожидания и сравнивая наши предсказания с действительностью. Когда мы формируем ожидания, которые оказываются правильными, мы испытываем удовольствие и удовлетворение. Эти механизмы вознаграждения поощряют успешное обучение. Также они стимулируют наше чувство прекрасного – а на самом деле они и есть это чувство.

Суммируя все эти наблюдения, мы обнаруживаем объяснение того, почему мы находим интересные явления (явления, благодаря которым мы узнаем что-то новое!) в физике красивыми. Важное следствие состоит в том, что мы особенно ценим опыт, который нас удивляет, но удивляет не слишком сильно. Стандартное, поверхностное узнавание не потребует от нас усилий и не сможет быть вознаграждено так же, как активное обучение. В то же время явления, значение которых мы совсем не можем понять, также не принесут нам удовольствия; это помехи.

И здесь нам тоже повезло в том, что Природа использует в своей основе симметрию и экономию средств: ведь эти принципы, так же как наше интуитивное понимание света, способствуют успешным предсказаниям и обучению. По внешнему виду части симметричного объекта мы можем предсказать (успешно!) внешний вид остальной его части; по поведению частей объектов природы мы можем предсказать (иногда успешно!) поведение целых объектов. Следовательно, симметрия и экономия средств – это как раз то, что мы хорошо приспособлены воспринимать как красоту.

Новые идеи и интерпретации

Вместе с новым взглядом на некоторые очень старые и некоторые не столь старые идеи вы найдете в этой книге и несколько идей существенно новых. Здесь я бы хотел упомянуть некоторые из самых важных.

Мое представление Главной теории как геометрии и мои размышления о следующих шагах за ее пределы являются адаптацией моих работ в фундаментальной физике. Эти работы, конечно же, основаны на работах многих других людей. Новым, насколько мне известно, является применение цветовых полей в качестве примера дополнительных измерений и мое использование тех возможностей, которые они открывают для иллюстрации локальной симметрии.

Моя теория о том, что поощрение обучения лежит в основе нашего чувства прекрасного в важных случаях и является его эволюционной причиной, а также приложение этой теории к музыкальной гармонии, которое предлагает рациональное объяснение открытий Пифагора в музыке, составляют созвездие идей, которыми я долгое время развлекался частным образом и которые впервые представляю публике здесь. Будьте бдительны!

Мои рассуждения о расширении цветового восприятия основано на идущих в настоящее время практических исследованиях, которые, как я надеюсь, приведут к появлению коммерческих продуктов и которые защищены патентами.

Я хотел бы думать, что Нильс Бор поддержал бы мою широкую интерпретацию дополнительности, и мог бы даже признать свое авторство – но не уверен, что он бы это сделал.

Пифагор I: Мысль и объект

Эфемерный Пифагор

Человек по имени Пифагор жил примерно в 570–495 гг. до н. э., но о нем известно очень мало. Или, вернее, о нем «известно» очень много, но бóльшая часть этих фактов наверняка ошибочна, потому что документальные свидетельства его жизни полны противоречий. В них сочетаются возвышенное, смешное, невероятное и даже полная нелепица.

Говорили, что Пифагор был сыном Аполлона, имел золотое бедро и светился. Возможно, он был сторонником вегетарианства, хотя вполне может быть, что все было наоборот. Среди его самых известных высказываний дурную славу приобрел запрет есть бобы, потому что «у бобов есть душа», хотя несколько ранних источников недвусмысленно отрицают, что Пифагор когда-либо говорил или верил во что-то подобное. Более определенно можно сказать, что Пифагор верил в переселение душ и проповедовал это учение. Существует несколько историй, которые подтверждают это, хотя каждая из них, конечно, вызывает сомнения. Согласно Авлу Геллию[4], Пифагор помнил четыре свои прошлые жизни, в том числе ту, в которой он был прекрасной куртизанкой по имени Алко. Ксенофан вспоминал, что Пифагор, услышав скулеж собаки, которую били, бросился остановить ее обидчика, заявив, что узнал голос умершего друга. Также Пифагор, как и святой Франциск столетия спустя, поклонялся животным.

Стэнфордская энциклопедия философии – кстати, бесплатный и чрезвычайно полезный сетевой ресурс – подытоживает все это в следующем виде:

В современности сложился известный образ Пифагора как ведущего математика и ученого. Тем не менее дошедшие из древности свидетельства говорят о том, что, хотя Пифагор был известен в годы своей жизни и даже 150 лет спустя после смерти, во времена Платона и Аристотеля, его слава не была связана с математикой или наукой. Он был знаменит как:

1) знаток того, что происходит с душой после смерти, считавший, что душа бессмертна и переживает многочисленные реинкарнации;

2) знаток религиозных ритуалов;

3) чудодей, у которого было золотое бедро и который мог быть в двух местах одновременно;

4) основоположник аскетического образа жизни, включающего в себя ограничения в пище, религиозные ритуалы и суровую самодисциплину.

Некоторые факты выглядят более ясными. Реальный Пифагор родился на греческом острове Самосе, много путешествовал и стал вдохновителем и создателем необычного религиозного движения. Его братство посвященных процветало в течение недолгого времени в Кротоне, в Южной Италии, и имело несколько ответвлений в других провинциях, пока не было повсеместно запрещено. Пифагорейцы организовывали тайные общества, вокруг которых сосредотачивалась жизнь братьев. Эти общины, включающие и мужчин, и женщин, способствовали появлению некого вида интеллектуального мистицизма, который казался современникам удивительным и великолепным, хотя и пугающе необычным. Их взгляды на мир сосредоточились вокруг молитвенного восхищения числами и музыкальной гармонией, которые они считали отражением глубинной структуры реальности. Как мы увидим далее, в какой-то мере это имело отношение к действительности.

Настоящий Пифагор

Снова приведем цитату из Стэнфордской энциклопедии:

Портрет Пифагора, который вырисовывается из этих свидетельств, показывает нам не математика, который приводит строгие доказательства, и не ученого, который проводит эксперименты, чтобы открыть природу естественного мира, а скорее, какого-то человека, который придает особое значение и приписывает особую роль математическим соотношениям, которые были известны и до него.

Бертран Рассел более лаконичен:

Это смесь Эйнштейна и Мэри Бейкер Эдди[5].

Для ученых, изучающих настоящую биографию Пифагора, самой большой проблемой является тот факт, что последователи Пифагора приписывали ему свои собственные мысли и открытия. Очевидно, так они надеялись одновременно придать вес своим идеям и улучшить репутацию Пифагора, чтобы развивать свою общину – ту, которую он основал. Таким образом, блестящие открытия в математике, физике, музыке, а также вдохновляющий мистицизм, плодотворная философия и чистая мораль были все связаны с образом одной богоподобной фигуры. Эта приводящая в священный трепет фигура и стала для нас настоящим Пифагором.

Нельзя сказать, что совершенно неприемлемо приписывать заслуги эфемерного Пифагора (оставшегося в истории) настоящему Пифагору, поскольку великие достижения в математике и физике, совершенные настоящим Пифагором, проистекали из образа жизни, на который мнимый Пифагор вдохновил своих последователей, и из общины, которую тот создал.

(Если угодно, вы можете провести параллели с тем, как по-разному складывается судьба других крупных религиозных деятелей при жизни и после.)

Благодаря Рафаэлю мы знаем, как мог выглядеть настоящий Пифагор. На цветной вклейке, на иллюстрации B мы видим, как он, окруженный почитателями, сосредоточенно записывает что-то в большой книге.

«Число есть сущность всех вещей»

Очень трудно разобрать, что же там пишет Пифагор, но мне нравится думать, что это какой-то вариант его фундаментального кредо:

«Число есть сущность всех вещей»[6].

Очень трудно понять сквозь разделяющую нас огромную пропасть во времени и пространстве, что же именно он имел в виду под этой фразой. Так что здесь нам придется дать волю своему воображению.

Теорема Пифагора

Начнем с того, что на Пифагора неизгладимое впечатление произвела теорема, впоследствии названная его именем. Впечатление было настолько огромным, что из-за этого открытия он нарушил принципы вегетарианства и заказал гекатомбу – ритуальное жертвоприношение сотни быков, за которым следовал пир. Это было сделано в знак благодарности музам.

Из-за чего же был весь шум?

Теорема Пифагора – это утверждение, касающееся прямоугольных треугольников, т. е. треугольников, имеющих угол, равный 90°, иначе говоря, прямой угол. Теорема гласит, что если построить квадраты на разных сторонах такого треугольника, то сумма площадей двух меньших квадратов будет равна площади большего. Классический пример – это прямоугольный треугольник со сторонами 3-4-5, изображенный на илл. 1.

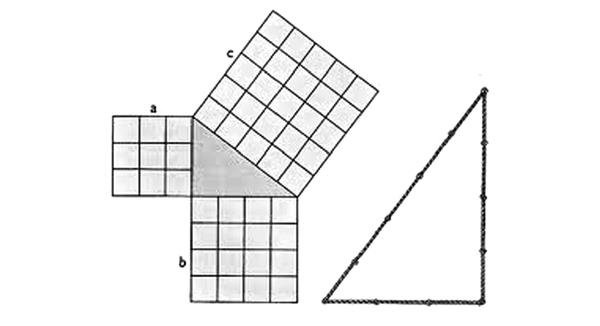
Илл. 1. Прямоугольный треугольник со сторонами 3-4-5, простейший случай теоремы Пифагора

Площади двух меньших квадратов составляют 32 = 9 и 42 = 16, как мы можем это увидеть, если в духе Пифагора подсчитаем количество маленьких квадратиков, на которые разбиты фигуры. Площадь большого квадрата составляет 52 = 25. И мы можем проверить: 9 + 16 = 25.

Сейчас теорема Пифагора знакома большинству из нас, хотя бы как смутное воспоминание из школьного курса геометрии. Но если вы услышите заново – ушами Пифагора, так сказать, – содержащееся в ней послание, вы поймете нечто потрясающее. Эта теорема гласит, что геометрия объектов воплощает скрытые численные отношения. Иными словами, она говорит, что Числами можно описать пусть не все, но по крайней мере нечто очень важное в физической реальности, а именно размеры и формы объектов, составляющих ее.

Позднее в этой медитации мы будем иметь дело с гораздо более продвинутыми и сложными концепциями, и мне придется прибегать к метафорам и аналогиям, чтобы передать их значение. Та особая радость, которую ученый находит, когда мыслит четкими математическими категориями, а точно определенные понятия идеально подходят друг к другу, теряется при такой передаче. Но сейчас у нас есть возможность испытать эту особую радость. Часть волшебства теоремы Пифагора состоит в том, что ее можно доказать, имея минимальную подготовку. Самые лучшие ее доказательства незабываемы, и воспоминание о них остается на всю жизнь. Они вдохновляли Олдоса Хаксли и Альберта Эйнштейна – не говоря уж о самом Пифагоре! – и, надеюсь, вдохновят и вас.

Доказательство Гвидо

«Так просто!»

Именно эти слова произнес Гвидо, юный герой рассказа Олдоса Хаксли «Молодой Архимед», описывая свое доказательство теоремы Пифагора. Доказательство Гвидо основывается на формах, изображенных на цветной вклейке (иллюстрация С).

Забава Гвидо

Давайте разберем то, что было очевидно для Гвидо с первого взгляда.

Каждый из двух больших квадратов, разделенных на части, содержит четыре цветных треугольника, и они одинаковы в обоих больших квадратах. Все цветные треугольники являются прямоугольными треугольниками, и все они имеют одинаковый размер. Будем считать, что длина самой короткой стороны есть a, следующей по длине – b, а самой длинной (гипотенузы) – с. Тогда легко заметить, что стороны двух больших квадратов имеют длину a + b, и далее, что эти два квадрата равны по площади. Таким образом, не вошедшие в треугольники части больших квадратов тоже должны иметь равные площади.

Но из чего состоят эти равные площади? В первом большом квадрате, слева, у нас есть синий квадрат со стороной a и красный квадрат со стороной b. Они имеют площади a² и b². Во втором большом квадрате, справа, у нас есть серый квадрат со стороной c. Его площадь равна c². Вспомнив то, о чем говорилось в предыдущем абзаце, мы можем прийти к выводу, что a² + b² = c².

А это и есть теорема Пифагора!

Доказательство Эйнштейна (?)

В своих автобиографических записках Эйнштейн вспоминает:

Помню, дядя рассказал мне о теореме Пифагора еще до того, как священная книжка по геометрии попала мне в руки. В результате многочисленных усилий мне удалось добиться успеха в «доказательстве» этой теоремы на основании подобия треугольников; таким образом мне казалось «очевидным», что соотношение сторон в прямоугольном треугольнике должно определяться одним из острых углов.

В этой записи действительно недостаточно деталей, чтобы с полной достоверностью реконструировать доказательство Эйнштейна, но ниже, на илл. 2, приведено мое наилучшее предположение. Оно претендует на правильность, поскольку является самым простым и самым красивым доказательством теоремы Пифагора. В частности, это доказательство делает совершенно понятным, почему именно квадраты сторон задействованы в этой теореме.

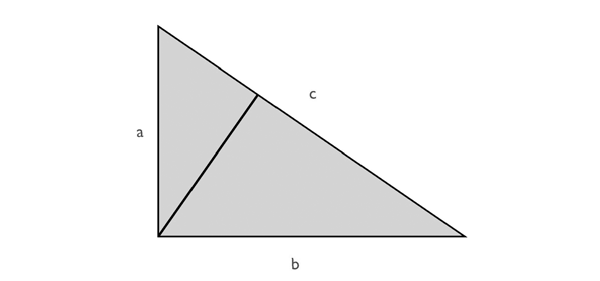
Илл. 2. Вероятная реконструкция доказательства Эйнштейна из автобиографических записок

Отполированная драгоценность

Мы начинаем с наблюдения о том, что прямоугольные треугольники, которые имеют общий угол φ, являются подобными друг другу в строгом смысле, т. е. вы можете перейти от одного к другому с помощью изменения масштаба (увеличения или сжатия). Кроме того, если мы изменим длину стороны треугольника, умножив ее на какой-либо коэффициент, то его площадь изменится в количество раз, равное квадрату этого коэффициента. Теперь рассмотрим три прямоугольных треугольника, показанных на илл. 2: всю фигуру и два треугольника, которые она включает в себя. Каждый из этих треугольников содержит угол φ, следовательно, они подобны. Вследствие этого их площади пропорциональны a², b², c² в порядке от самого маленького к самому большому. Но так как два меньших треугольника составляют большой треугольник, соответствующие площади также должны суммироваться, поэтому

a² + b² = c².

И теорема Пифагора тут как тут!

Прекрасная насмешка

Прекрасная насмешка состоит в том, что теорема Пифагора может быть использована, чтобы подорвать его доктрину о том, что число есть сущность всех вещей. Такой возмутительный вывод следует из одного открытия пифагорейской школы, которое приписывали не Пифагору, а его ученику Гиппаcу. Вскоре после того, как он сделал это открытие, Гиппаc утонул в море. Не известно, была ли его смерть вызвана волей богов или волей пифагорейцев. Доказательство Гиппаcа очень хорошо продумано, но не является слишком сложным. Давайте с ним ознакомимся.

Рассмотрим равнобедренные прямоугольные треугольники, у которых два катета равны, т. е. a = b. Теорема Пифагора гласит, что 2 × a² = c².

Теперь предположим, что длины сторон а и с выражаются целыми числами. Если все вещи – числа, то лучше бы это было так! Но выясняется, что это невозможно. Если и а, и с – четные числа, мы можем рассмотреть подобный треугольник, составляющий половину от размера первоначальной фигуры. Мы можем продолжать уменьшать его каждый раз в два раза, пока не получим треугольник, где по крайней мере одно из значений (а или с) является нечетным.

Но какой бы выбор мы ни сделали, мы быстро достигнем противоречия. Вначале давайте предположим, что с выражается нечетным числом. Тогда c² также является нечетным. Но 2 × a² явно дает четное число, поскольку содержит множитель 2. Таким образом, у нас не получается равенства 2 × a² = c², как гласит теорема Пифагора. Противоречие!

Предположим тогда, что с выражается четным числом, – скажем, с = 2 × p. Тогда c² = 4 × p². Теорема Пифагора говорит нам (после того, как мы разделим обе части равенства на 2), что a² = 2 × p². Следовательно, а не может выражаться нечетным числом – по тем же причинам, что и выше. Противоречие!

Таким образом, все-таки не все вещи могут быть выражены целыми числами. Не может существовать никакого атома длины, из которого могут быть выведены все возможные длины как произведение целого числа на этот самый атом.

Кажется, пифагорейцы не представляли себе, что можно прийти к другому умозаключению и сохранить неприкосновенной идею о том, что все вещи есть числа. В конце концов, можно представить себе мир, где все пространство состоит из множества одинаковых неделимых частей. Например, мои друзья Эд Фредкин и Стивен Вольфрам продвигают модели нашего мира, основанные на клеточных автоматах, которые обладают именно этим свойством. И монитор вашего компьютера, изображение на котором состоит из точек света, называющихся пикселями, доказывает, что такой мир может выглядеть достаточно реалистично! Если рассуждать логически, справедливо было бы прийти к выводу, что в таком мире невозможно построить правильный равнобедренный прямоугольный треугольник. В нем обязательно что-то будет немного не так. Или прямой угол будет немного отклоняться от 90°, или катеты будут не совсем равны или – как на экране монитора – стороны такого треугольника будут не совсем прямыми.

Но такой подход не был близок греческим математикам. Они-то рассматривали геометрию в наиболее соблазнительной, непрерывной форме, где сосуществуют в точности прямые углы и точное равенство сторон. (Этот подход также оказался самым плодотворным для физиков, как мы увидим на примере Ньютона.) Чтобы утвердить такую точку зрения, грекам пришлось установить приоритет геометрии над арифметикой, потому что – как мы уже видели – целые числа не могут адекватно описать даже очень простую геометрическую фигуру. Таким образом, они отказались от буквы доктрины о том, что все вещи есть числа, но не от ее духа.

Мысль и объект

Истинная сущность кредо Пифагора – это не буквальное утверждение того, что мир должен воплощать целые числа, но оптимистичное убеждение в том, что мир должен воплощать красивые понятия.

Урок, за который Гиппас заплатил жизнью, состоит в том, что мы должны стремиться узнать у Природы, в чем состоят ее правила. В этом предприятии скромность является необходимой чертой. Геометрия не менее красива, чем арифметика. На самом деле она более естественно подходит для нашего мозга, который во многом нацелен на обработку визуальных образов, и большинство людей предпочитают именно ее. И геометрия не содержит в себе меньше идей, меньше чистой работы ума, чем арифметика. Большая часть древнегреческой математики, систематизированная в «Началах» Евклида, стремилась доказать именно то, что геометрия – это логическая система.

Продолжив нашу медитацию, мы обнаружим, что Природа изобретательна в своем языке. Она поражает наше воображение новыми видами чисел, новыми видами геометрических форм – и даже, в квантовом мире, новыми видами логики.

Пифагор II: Число и гармония

Сущность всех струнных инструментов, будь это древняя лира или современная гитара, виолончель или пианино, одинакова: они производят звук с помощью движения струн. Качество звука, или тембр, зависит от множества сложных факторов, в том числе от материала струн, формы поверхности деки – «звукоотражателя», вибрирующего согласованно со струной, и способа извлечения звука из струны: щипком, проведением смычка или ударом. Но для всех инструментов существует основной тон или строй, который мы, слушая игру на них, распознаем как ноты. Пифагор – настоящий Пифагор – открыл, что музыкальный строй подчиняется двум удивительным правилам. Эти правила имеют прямую связь с числами, свойствами физического мира и нашим чувством гармонии (которая является одним из ликов красоты).