
Полная версия
Human Universe
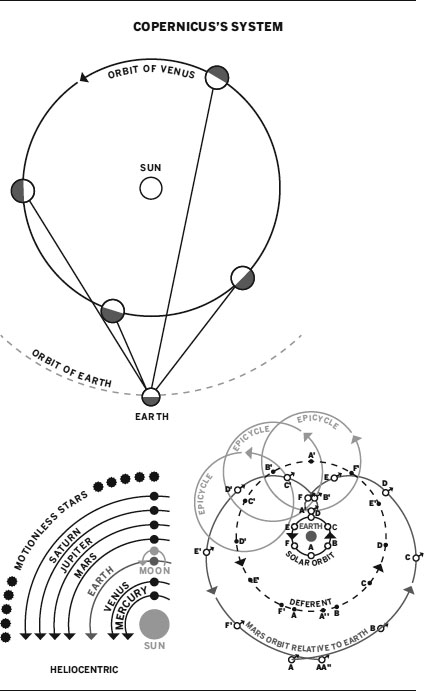
At first sight it is difficult to understand why Ptolemy’s contrived mess lasted so long, but there is a modern bias to this statement that is revealing. Today, a scientifically literate person assumes that there is a real, predictable universe beyond Earth that operates according to laws of nature – the same laws that objects obey here on Earth. This idea, which is correct, only emerged fully formed with the work of Isaac Newton in the 1680s, over a century after Copernicus. Ancient astronomers were interested primarily in predictions, and although the nature of physical reality was debated, the central scientific idea of universal laws of physics had simply not been discovered. Ptolemy created a model that makes predictions that agree with observation to a reasonable level of accuracy, and that was good enough for most people. There had been notable dissenting voices, of course – the history of ideas is never linear. Epicurus, writing around 300 BCE, proposed an eternal cosmos populated by an infinity of worlds, and around the same time Aristarchus proposed a Sun-centred universe about which the Earth and planets orbit. There was also a strong tradition of classic orthodoxy in the Islamic world in the tenth and eleventh centuries. The astronomer and mathematician Ibn al-Haytham pointed out that, whilst Ptolemy’s model had predictive power, the motions of the planets as shown in the figure here represent ‘an arrangement that is impossible to exist’.
The end of the revolution started by Copernicus around 1510, and the beginning of modern mathematical physics, can be dated to 5 July 1687, when Isaac Newton published the Principia. He demonstrated that the Earth-centred Ptolemaic jumble can be replaced by a Sun-centred solar system and a law of universal gravitation, which applies to all objects in the universe and can be expressed in a single mathematical equation:
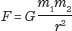
The equation says that the gravitational force between two objects – a planet and a star, say – of masses m1 and m2 can be calculated by multiplying the masses together, dividing by the square of the distance r between them, and multiplying by G, which encodes the strength of the gravitational force itself. G, which is known as Newton’s Constant, is, as far as we know, a fundamental property of our universe – it is a single number which is the same everywhere and has remained so for all time. Henry Cavendish first measured G in a famous experiment in 1798, in which he managed (indirectly) to measure the gravitational force between lead balls of known mass using a torsion balance. This is yet another example of the central idea of modern physics – lead balls obey the same laws of nature as stars and planets. For the record, the current best measurement of G = 6.67 × 10-11 N m2/kg2, which tells you that the gravitational force between two balls of mass 1kg each, 1 metre apart, is just less than ten thousand millionths of a Newton. Gravity is a very weak force indeed, and this is why its strength was not measured until 71 years after Newton’s death.
NEWTON’S LAW OF GRAVITY
F
Force between the masses
G
Gravitational constant
m1
First mass
m2
Second mass
r
Distance between the centres of the masses

This is a quite brilliant simplification, and perhaps more importantly, the pivotal discovery of the deep relationship between mathematics and nature which underpins the success of science, described so eloquently by the philosopher and mathematician Bertrand Russell: ‘Mathematics, rightly viewed, possesses not only truth, but supreme beauty – a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as in poetry.’
Nowhere is this sentiment made more clearly manifest than in Newton’s Law of Gravitation. Given the position and velocity of the planets at a single moment, the geometry of the solar system at any time millions of years into the future can be calculated. Compare that economy – you could write all the necessary information on the back of an envelope – with Ptolemy’s whirling offset epicycles. Physicists greatly prize such economy; if a large array of complex phenomena can be described by a simple law or equation, this usually implies that we are on the right track.
The quest for elegance and economy in the description of nature guides theoretical physicists to this day, and will form a central part of our story as we trace the development of modern cosmology. Seen in this light, Copernicus assumes even greater historical importance. Not only did he catalyse the destruction of the Earth-centred cosmos, but he inspired Brahe, Kepler, Galileo, Newton and many others towards the development of modern mathematical physics – which is not only remarkably successful in its description of the universe, but was also necessary for the emergence of our modern technological civilisation. Take note, politicians, economists and science policy advisors of the twenty-first century: a prerequisite for the creation of the intellectual edifice upon which your spreadsheets, air-conditioned offices and mobile phones rest was the curiosity-driven quest to understand the motions of the planets and the Earth’s place amongst the stars.
AT THE CENTRE OF THE SOLAR SYSTEM
Matching the observations of the wandering stars – the planets – of the night sky with the idea that the Earth was at the centre of the solar system required extremely complex models. In the case of Venus, combining the Earth at the centre with the observations meant that Venus had a circular orbit around a point midway between the Earth and the Sun, so-called epicycles, with all the other planets having similar complicated orbits around various points scattered around the solar system. Placing the Sun at the centre of the solar system, with the planets arranged in their familiar order, with the Moon orbiting the Earth, gave a much simpler system.

CHANGING PERSPECTIVE
1968 was a difficult year on planet Earth. The Vietnam War, the bloodiest of Cold War proxy tussles, was at its height, ultimately claiming over three million lives. Martin Luther King Jr. was assassinated in Memphis, prompting presidential hopeful Bobby Kennedy to ask the people of the United States ‘to tame the savageness of man and make gentle the life of this world’. Kennedy himself was assassinated before the year was out. Elsewhere, Russian tanks rolled into Prague, and France teetered on the edge of revolution. As I approached my first Christmas, my parents could have been forgiven for wondering what kind of world their son would inhabit in 1969. And then, as Christmas Eve drifted into Christmas morning, an unexpected snowfall decorated Oakbank Avenue and Borman, Lovell and Anders, 400,000 kilometres away, saved 1968.
Apollo 8 was, in the eyes of many, the Moon mission that had the most profound historical impact. It was a terrific, noble risk; a magnificent roll of the dice; a distillation of all that is great about exploration; a tribute to the sheer balls of the astronauts and engineers who decided that, come what may, they would honour President Kennedy’s pledge to send ‘a giant rocket more than 300 feet tall, the length of this football field, made of new metal alloys, some of which have not yet been invented, capable of standing heat and stresses several times more than have ever been experienced, fitted together with a precision better than the finest watch, carrying all the equipment needed for propulsion, guidance, control, communications, food and survival, on an untried mission, to an unknown celestial body, and then return it safely to Earth, re-entering the atmosphere at speeds of over 40,000 kilometres per hour, causing heat about half that of the temperature of the Sun – almost as hot as it is here today – and do all this, and do it right, and do it first before this decade is out’. If I heard that from a leader today I’d be first on the rocket. Instead I have to listen to vacuous diatribes about ‘fairness’, ‘hard-working families’, and how ‘we’re all in it together’. Sod that, I want to go to Mars.
To set Apollo 8 in context, Apollo 7, the first manned test flight of the Apollo programme, was flown by Schirra, Eisele and Cunningham in October 1968. Apollo 8 was supposed to be a December test flight for the Lunar Lander, conducted in the familiar surroundings of Earth orbit, but delivery delays meant that it was not ready for flight and the aim of meeting Kennedy’s deadline looked to be dead. But this wasn’t the twenty-first century, it was the 1960s and NASA was run by engineers. The programme manager was George Low, an army veteran and aeronautical engineer who knew the spacecraft inside out and had the strength of character to make decisions. Why not send Apollo 8 directly to the Moon without the Lunar Lander, proposed Low, allowing Apollo 9 to test-fly the LEM (Lunar Excursion Module) in Earth orbit in early 1969 when it became available and pave the way for a landing before the decade was out? Virtually every engineer at NASA is said to have agreed, and so it was that only the second manned flight of the Apollo spacecraft lifted off from Kennedy on 21 December, ten short weeks after Apollo 7, bound for the Moon. The crew later said that they estimated their chance of succeeding to be fifty-fifty.
Borman: Oh my God!
Look at that picture over there.
Here’s the Earth coming up.
Wow, is that pretty.
Anders: Hey, don’t take that,
it’s not scheduled.
Borman: (laughing) You got a color film, Jim?
Anders: Hand me that roll of color quick, will you …?
Lovell: Oh, man, that’s great!
Precisely 69 hours, 8 minutes and 16 seconds after launch, the Command Module’s engine fired to slow the spacecraft down and allow it to be captured by the Moon’s gravity, putting the three astronauts into lunar orbit. Newton’s almost 300-year-old equations were used to calculate the trajectory. This was a spectacular, practically unbelievable engineering triumph. Less than a decade after Yuri Gagarin became the first human to orbit the Earth, three astronauts travelled all the way to the Moon. But the mission’s powerful and enduring cultural legacy rests largely on two very human actions by the crew. One was the famous and moving Christmas broadcast, the most-watched television event in history at that time, when distant explorers read the first lines from the Book of Genesis: ‘We are now approaching lunar sunrise, and for all the people back on Earth, the crew of Apollo 8 has a message that we would like to send to you,’ began Anders. ‘In the beginning God created the heaven and the Earth. And the Earth was without form, and void; and darkness was upon the face of the deep.’ Borman concluded with a sentence clearly spoken by a lonely man 400,000 kilometres from home. ‘And from the crew of Apollo 8, we close with goodnight, good luck, a Merry Christmas – and God bless all of you, all of you on the good Earth.’
The mission’s most potent legacy, however, is NASA image AS8-14-2383, snapped by Bill Anders on a Hasselblad 500 EL at f/11 and a shutter speed of 1/250th of a second on Kodak Ektachrome film. It was, in other words, a very bright photograph. The image is better known as Earthrise. When viewed with the lunar surface at the bottom, Earth is tilted on its side with the South Pole to the left, and the equator running top to bottom. Little landmass can be seen through the swirling clouds, but the bright sands of the Namib and Saharan deserts stand out salmon pink against the blackness beyond. Just 368 years and 10 months after a man was burned at the stake for dreaming of worlds without end, here is Earth, a fragile crescent suspended over an alien landscape, the negative of a waxing Moon in the friendly skies of Earth. This is an unfamiliar, planetary Earth, no longer central; just another world. When Kennedy spoke of Apollo as a journey to an unknown celestial body, he meant the Moon. But we discovered Earth and, in the words of T. S. Eliot, came to know the place for the first time.
OUTWARDS TO THE MILKY WAY
Newton’s laws are the keys to understanding our place in our local neighbourhood. Coupled with precision observations of the motion of the planets and moons, they allow the scale and geometry of the solar system to be deduced, and their positions to be calculated at any point in the future. The nature and location of the stars, however, requires an entirely different approach because at first sight they appear to be point-like and fixed. The observation that the stars don’t appear to move is important if you know something about parallax, as the ancients did. Parallax is the name given to a familiar effect. Hold your finger up in front of your face and alternately close each of your eyes, keeping your finger still. Your finger appears to move relative to the more distant background, and the closer your finger is to your face, the more it appears to move. This is not an optical illusion; it’s a consequence of viewing a nearby object from two different spatial positions; in this case the two slightly different positions of your eyes. We don’t normally perceive this parallax effect because the brain combines the inputs from the eyes to create a single image, although the information is exploited to create our sense of depth. Aristotle used the lack of stellar parallax to argue that the Earth must be stationary at the centre of the universe, because if the Earth moved then the nearby stars would be observed to move against the background of the more distant ones. Thousands of years later, Tycho Brahe used a similar argument to refute the conclusions reached by Copernicus. Their logic was completely sound, but the conclusion is wrong because the nearby stars do move relative to the more distant background stars as the Earth orbits the Sun, and indeed as the Sun orbits the galaxy itself. You just have to look extremely carefully to see the effect.
Amongst the thousands of stars visible to the naked eye, 61 Cygni is one of the faintest. It’s not without interest, being a binary star system of two orange K-type dwarf stars, slightly smaller and cooler than the Sun, orbiting each other at the lethargic rate of around 700 years. Despite the pair’s relative visual anonymity, however, 61 Cygni has great historical significance. The reason for this quiet fame is that this faint star system was the first to have its distance from Earth measured by parallax.
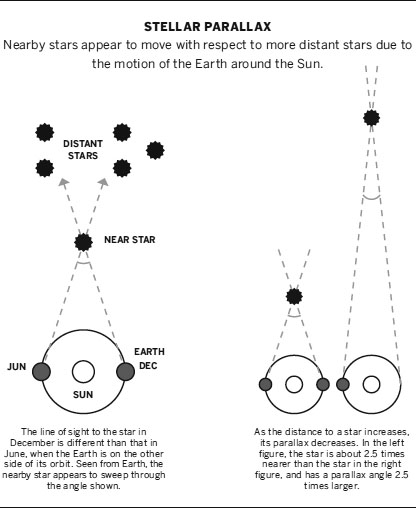
Friedrich Bessel is best known to a physicist or mathematician for his work on the mathematical functions that bear his name. Pretty much any engineering or physical problem that involves a cylindrical or spherical geometry ends up with the use of Bessel functions, and, in blissful ignorance, you will probably encounter some piece of technology that has relied on them in the design process at some point today. But Bessel was first and foremost an astronomer, being appointed director of the Königsberg Observatory at the age of only 25. In 1838, Bessel observed that 61 Cygni shifted its position in the sky by approximately two-thirds of an arcsecond over a period of a year as viewed from Earth. That’s not very much – an arcsecond is one 3600th of a degree. It is enough, however, to do a bit of trigonometry and calculate that 61 Cygni is 10.3 light years away from our solar system. This compares very favourably with the modern measurement of the distance, 11.41 ± 0.02 light years. Parallax is so important in astronomy that there is a measurement system completely based on it, which allows you to do these sums in your head. Astronomers use a distance measurement known as a parsec – which stands for ‘per arcsecond’. This is the distance of a star from the Sun that has a parallax of 1 arcsecond. One parsec is 3.26 light years. Bessel’s measurement of the parallax of 61 Cygni was 0.314 arcseconds, and this immediately implies that it’s around 10 light years away.
Even today, stellar parallax remains the most accurate way of determining the distance to nearby stars, because it is a direct measurement which uses only trigonometry and requires no assumptions or physical models. On 19 December 2013 the Gaia space telescope was launched on a Soyuz rocket from French Guiana. The mission will measure, by parallax, the positions and motions of a billion stars in our galaxy over five years. This data will provide an accurate and dynamic 3D map of the galaxy, which in turn will allow for an exploration of the history of the Milky Way, because Newton’s laws, which govern the motions of all these stars under the gravitational pull of each other, can be run backwards as well as forwards in time. Given precise measurements of the positions and velocities of 1 per cent of the stars in the Milky Way, it is possible to ask what the configuration of the stars looked like millions or even billions of years ago. This enables astronomers to build simulations of the evolution of our galaxy, revealing its history of collisions and mergers with other galaxies over 13 billion years, stretching back to the beginning of the universe. Newton and Bessel would have loved it.
Stellar parallax, when deployed using a twenty-first-century orbiting observatory, is a powerful technique for mapping our galaxy out to distances of many thousands of light years. Beyond our galaxy, however, the distances are far too great to employ this direct method of distance measurement. In the mid-nineteenth century, this might have appeared an insurmountable problem, but science doesn’t proceed by measurement alone. As Newton so powerfully demonstrated, scientific progress often proceeds through the interaction between theory and observation. Newton’s Law of Gravitation is a theory; in physics this usually means a mathematical model that can be applied to explain or predict the behaviour of some part of the natural world. How might we measure the mass of a planet? We can’t ‘weigh’ it directly, but given Newton’s laws we can determine the planet’s mass very accurately if it has a moon. The logic is quite simple – the moon’s orbit clearly has something to do with the planet’s gravity, which in turn has something to do with its mass. These relationships are encoded in Newton’s law, and careful observation of the moon’s orbit around the planet therefore allows for the planet’s mass to be determined. For the more mathematical reader, the equation is:
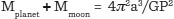
where a is the (time-averaged) distance between the planet and the moon, G is Newton’s gravitational constant and P is the period of the orbit. (This equation is in fact Kepler’s third law, discovered empirically by Kepler in 1619. Kepler’s laws can be derived from Newton’s law of gravitation.) Under the assumption that the mass of the planet is far larger than the mass of the Moon, this equation allows for the mass of the planet to be measured. This is how theoretical physics can be used to extract measurements from observation, given a mathematical model of the system. To measure the distance to objects that are too far away to use parallax, therefore, we need to find a theory or mathematical relationship that allows for a measurement of something – anything – to be related to distance. The first relationship of this type, which opened the door to all other methods of distance measurement out to the edge of the observable universe, was discovered at the end of the nineteenth century by an American astronomer named Henrietta Leavitt.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.







