Натуральные числа. Этюды, вариации, упражнения

Получение квадратных чисел можно иллюстрировать построением квадратов с последовательным увеличением длины стороны квадрата: 1, 4, 9, 16, 25, 36, 49, … .

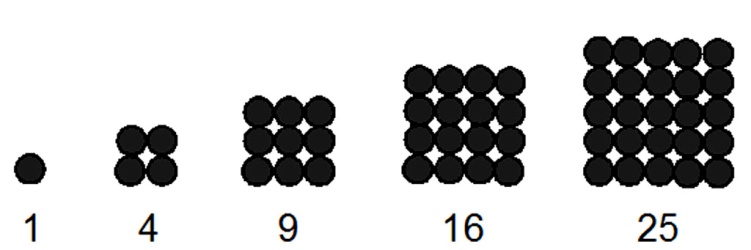
С алгебраической точки зрения они представляют собой квадраты чисел натурального ряда, но могут быть интерпретированы и как результат последовательного суммирования нечетных чисел натурального ряда: 1+3=4, 1+3+5=9, 1+3+5+7=16, 1+3+5+7+9=25. Формула для получения n-го квадратного числа Pn(4)=n2. Каждое квадратное число, кроме единицы, есть сумма двух последовательных треугольных чисел: 4=1+3, 9=3+6, 16=6+10, Pn(4)=Pn-1(3)+Pn(3). До сих пор не доказана гипотеза Лежандра (1808 год): между последовательными квадратными числами всегда найдётся простое число. Не доказана, но и не опровергнута.

Частным случаем плоских чисел являются прямоугольные числа, являющиеся произведением двух последовательных натуральных чисел: 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, … .

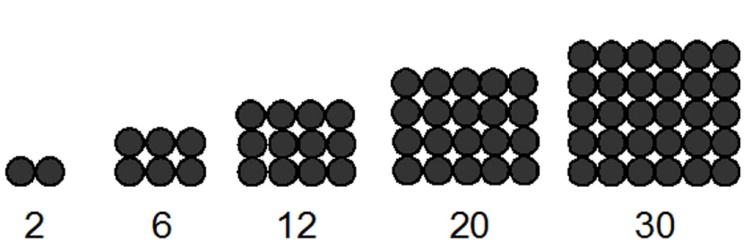
Прямоугольные числа представляют собой удвоенные треугольные числа: Pn(np)=n(n-1).

Вернемся к правильным многоугольникам. На очереди пятиугольные числа: 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, … .

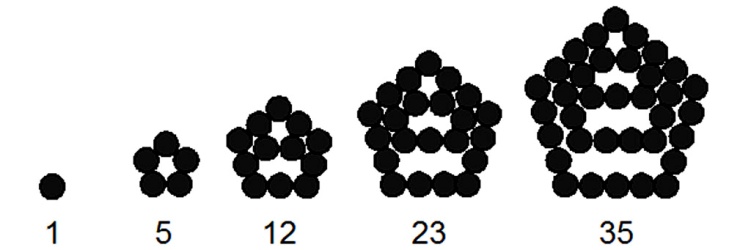
Формула для получения n-го пятиугольного числа: Pn(5)=(n(3n-1))/2.

Далее идут шестиугольные числа: 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, ….

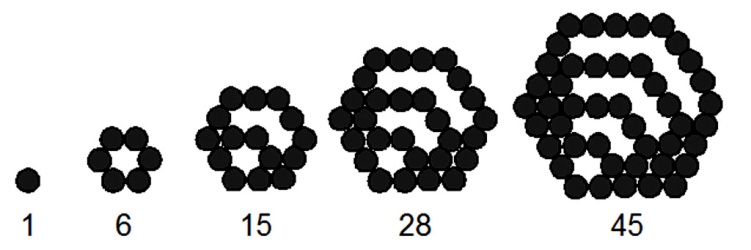
Формула для получения n-го шестиугольного числа: Pn(6)=2n2-n. Последовательность шестиугольных чисел получается из последовательности треугольных чисел вычёркиванием элементов с чётными номерами: Pn(6)=P2n-1(3).

Можно было бы продолжать бесконечно, рассматривая прочие многоугольные плоские фигурные числа, но нужно где-то остановиться. Пусть это будут шестиугольные числа.

Выйдя из плоскости можно рассмотреть трехмерные правильные фигурные числа. Пирамидальные числа возникают при складывании маленьких шаров одинакового диаметра горкой так, чтобы они не раскатывались. Получается пирамида. Первые из них тетраэдрические числа – это фигурные числа, которые представляют собой пирамиду, сложенную из сфер одного диаметра. Каждый слой в такой пирамиде – треугольное число. Наверху один шар, под ним – 3, под теми – 6 и т. д.: 1, 1+3=4, 1+3+6=10, 1+3+6+10=20, … . Пример нескольких первых тетраэдрических чисел: 1, 4, 10, 20, 35, 56, 84, 120, 165, … . Формула для тетраэдрического числа: Tn(4)=(n(n+1)(n+2))/6.

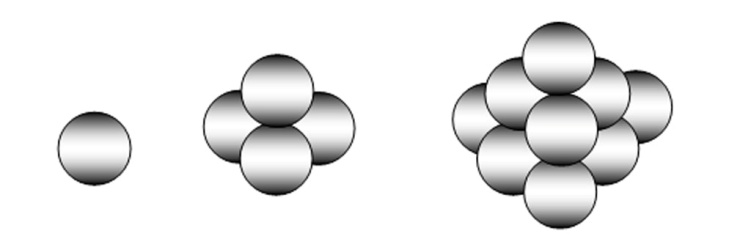
Затем к пирамидальным числам отнесем квадратные пирамидальные числа, представляющие собой количество сложенных сфер в пирамиде с квадратным основанием. И далее, далее … .

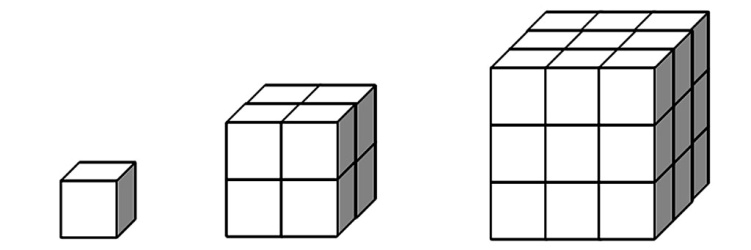
Кубические числа возникают при складывании кубиков: 1, 2·2·2=8, 3·3·3=27, 4·4·4=64, 5·5·5=125… , то есть это просто кубы натуральных чисел.

В любом рассмотренном варианте фигурных чисел возможны продолжения. Некоторые из них мы отнесли во второй уровень классификации и все равно перебрать это многообразие невозможно. Причем, у каждого из этих видов чисел открыты свои свойства, о которых здесь не рассказано. Целью этой книги не является подробное описание свойств всех существующих групп натуральных чисел. Задача ставится иная: легкими штрихами наметить общую картину, заинтересовать читателя, который возможно сам продолжит рассмотрение понравившегося ему класса чисел, и тогда уж изучит все их свойства по другим источникам, а возможно сделает свои открытия. Вот где простор для тематики ученической проектной деятельности. Каждому ученику поручить исследование отдельного вида чисел, их хватит на целый класс.

Столкнувшись с тем многообразием, которое скрыто в одних только натуральных числах, понимаешь, для чего могла бы пригодиться бесконечная жизнь – изучать эти числа.

С другой стороны, поставьте себя на место древних пифагорейцев. Телевизоров нет, смартфонов нет, развлечений кот наплакал. Поэтому они и развлекались с натуральными числами и достигли в этом таких высот, которые современный человек вряд ли охватит своим умом. Причем учтите, во времена пифагорейцев занимались математикой и философией люди свободные от других забот, не ведающие иного труда, кроме умственного. Даже в умственной деятельности теоретические исследования считались достойными привилегированного класса, а чисто вычислительная, практическая деятельность поручалась низшим сословиям. В наше время нет привилегированных классов и большинству людей не до чисел, ведь жизнь с развитием цивилизации легче не становится. Но как в любой другой области, среди множества людей разумных есть и любители исследовать числа.

Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания. Поэтому их изучением занимались многие математики античности (Эратосфен, Диофант), большой интерес к фигурным числам проявили индийские математики и первые математики средневековой Европы (Фибоначчи, Кардано), выдающиеся умы более позднего времени (Ферма, Эйлер, Гаусс). Все результаты, которых они достигли не описать и в нескольких книгах. В частности Диофант знал формулу, связывающую треугольные и квадратные числа: 8Pn(3)=Pn(4). Были выведены общие формулы представления n-го по порядку k-угольного числа. Ферма сформулировал в 1637 году так называемую «золотую теорему»: Всякое натуральное число – либо треугольное, либо сумма двух или трёх треугольных чисел.

Всякое натуральное число – либо квадратное, либо сумма двух, трёх или четырёх квадратных чисел.

Всякое натуральное число – либо пятиугольное, либо сумма от двух до пяти пятиугольных чисел; и т.д.

Полное доказательство этой теоремы сумел дать Коши в 1813 году. Оцените промежуток времени, потребовавшийся для доказательства одной теоремы: с 1637 до 1813 года.

Критерий – цифровое выражение числа

Последние годы в занимательной математике много пишется о числах, имеющих специфическое представление в виде цифр. В первую очередь речь идет о числах – палиндромах. Это понятие пришло в математику из языка, где палиндром (от греч. palindromos – бегущий обратно), слово, фраза или стих, которые могут читаться (по буквам или по словам) спереди назад и с конца вперед, давая одинаковый смысл. В русском языке палиндромами являются, например, такие слова: довод, доход, заказ, радар и другие. Некоторые палиндромы, если их написать печатными буквами, не только читаются одинаково слева направо и наоборот, но обладают осью симметрии, например, поп, потоп, топот. Палиндромы известны во многих языках (например, gig (кабриолет), eve (канун), level (уровень) – в английском), а их история восходит к временам незапамятным. Чтобы не нарушать принятый в книге принцип давать классам чисел название в виде прилагательного, назовем такие числа палинромическими числами.

В математике к понятию палиндрома нужен иной подход, нежели в языкознании, потому что, в отличие от слова, любое число, написанное произвольным набором цифр, имеет право на существование, например, 1234567890987654321 – вполне реальное число. А что в нем еще интересного, в чем его исключительность? Содержательная сторона, изюминка идеи отражения здесь отсутствует, посмотришь на это число, и скажешь: «Ну, и что?». Можно поставить вопрос так: найти квадраты целых чисел, которые неизменно читаются как слева направо, так и наоборот. Некоторые из них найти легко: 112=121, 1112=12321, 11112=1234321. Все получившиеся числа палиндромы, и данное правило применимо к любому числу единиц, не превосходящему девяти. Есть и другие случаи, но их найти труднее, например, 2642=69696, 8362=698896, 22852=5221225. Одним вопросом намечено целое направление для поиска числовых палиндромов с определенным смыслом. Есть палиндромы и среди кубов, например 113=1331, причем в большинстве случаев, если куб – палиндром, то и кубический корень из него – тоже палиндром. Поиск палиндромов среди пятых степеней, пока не дал результатов. Высказана гипотеза, согласно которой не существует чисел палиндромов вида xk при k>4 . Ее тоже кому-то нужно доказать или опровергнуть. Другой вопрос – сколько существует простых чисел палиндромов. Среди первых пятидесяти простых чисел я нашел шесть палиндромов: 11, 101, 131, 151, 181, 191. Сколько их всего – неизвестно! Высказывалось предположение о том, что простых чисел палиндромов бесконечно много, но эта гипотеза пока не доказана. Таким образом, в математике числовые палиндромы кроме своей специфической записи должны обладать каким-то еще интересным свойством, чтобы заслуживать внимание.

В свою очередь среди чисел палиндромов выделяются так называемые моноцифровые числа. Это если определять их более-менее по-русски (хотя какое моно русское слово?). По-английски они называются репдигит или репдиджит в зависимости от того, как мы прочитаем английскую запись (от англ. repdigit – repeated digit – повторение цифры). Вы уже поняли, что это числа, в записи которых повторяется одна цифра: 11111, 222222, 33333. Среди них в свою очередь выделяются числа репьюниты – натуральные числа, запись которых состоит из единиц (от repeated unit - повторённая единица). Термин репьюнит был придуман в 1966 году Альбертом Х. Бейлером в его книге «Recreations in the theory of numbers: the queen of mathematics entertains». Для них принято сокращенное обозначение в виде Rn: R1=1, R2=11, R3=111 и т. д. Получаем последовательность: 1, 11; 111; 1111; 11111; 1111111 … . Обидно, но приходится употреблять эти неудобоваримые названия, которые неблагозвучны на русском языке и мне не очень нравятся, в отличие от самих чисел, вынужденных носить эти «репы». Для палиндромов придумали русское название – перевертень. Звучит хорошо, но почему-то не прижилось, а везде употребляется слово палиндром. Ничего не имею против взаимопроникновения языков. Мне только не нравится, что в основном это они в нас проникают. В моноцифровых числах много интересного, занимательного, поэтому о них еще поговорим в других разделах книги.

Еще один вид чисел, зависящих от входящих в них цифр – это стробограммные числа. Стробограммное число – это число, которое будучи записано на листе бумаги выглядит одинаково при повороте листа на 180 градусов. Например, 69, 96, 1001. Следует сделать небольшое замечание относительно записи единицы. Ее хвостик слева вверху немного портит картину, но принято на него не обращать внимание. При записи с использованием стандартных символов числа 0, 1, 8 симметричны вокруг горизонтальной оси, а 6 и 9 одинаковы друг с другом при повороте на 180 градусов. В такой системе записи первыми стробограммными числами являются: 1, 8, 11, 69, 88, 96, 101, 111, 181, 609, 619, 689, 808, 818, 888, 906, 916, 986, 1001, 1111, 1691, 1881, … .

Подобные числа входят в круг интересов любителей занимательной математики, а профессиональные математики, как правило, не занимаются ими. Стробограммные свойства данного числа зависят от шрифта. Например, в семисегментном изображении на электронных часах цифры 2 и 5 имеют центральную симметрию. Самый последний перевернутый год был 1961, А до этого последовательно 1881 и 1691.

Тетрадные или четырехполюсные числа – это числа, которые остается неизменными при отражении относительно горизонтальной или вертикальной оси симметрии, а также при центральной симметрии. Единственными цифрами, которые остаются теми же, если перевернуты вверх-вниз или зеркально отражены, являются 0, 1 и 8, поэтому тетрадное число-это палиндромическое число, содержащее только 0, 1 и 8 в качестве цифр. Первые несколько тетрадных чисел: 1, 8, 11, 88, 101, 111, 181, 808, 818, … . Четырехсторонняя симметрия объясняет название, поскольку tetra – это греческое число четыре. Тетрадные числа являются одновременно стробограммными и палинромическими. Более крупное тетрадное число всегда может быть сгенерировано путем добавления другого тетрадного числа к каждому концу исходного числа, сохраняя симметрию.

Наименования подмножеств натуральных чисел выражаются не только прилагательными, но и именами собственными. В дальнейшем имена собственные будет встречаться чаще.

Числа Цукермана - такие натуральные числа, которые делятся на произведение своих цифр. В честь какого Цукермана названы эти числа мне не удалось выяснить. Фамилия довольно распространенная и в русской интерпретации превращается в фамилию Сахаров. Определение этих чисел приведено в книге James J. Tattersall «Elementary Number Theory in Nine Chapters» издательства Кэмбриджского университета, 1999 года. Например, 135 – число Цукермана, так как 1+3+5=9; 135/9=15. Все целые числа от 1 до 9 являются числами Цукермана. Все числа, включающие ноль, не являются числами Цукермана, так как произведение их цифр равно нулю, а деление на ноль невыполнимо. Первые несколько чисел Цукермана, состоящие более чем из одной цифры: 11, 12, 15, 24, 36, 111, 112, 115, 128, 132, 135, 144, 175, 212, 216, 224, 312, 315, 384 … .

Числа Цукермана не могут содержать более чем восемь различных цифр, так как цифра 5 не может совмещаться ни с одной четной цифрой. Произведение четной цифры и 5 даст число, кратное 10, а исходное число не содержит цифры 0, следовательно, не может делиться на 10. Наименьшее число Цукермана, содержащие восемь различных цифр – это 1196342784. В свою очередь числа Цукермана это подмножество обнаженных чисел (извините, но есть и такие).

Натуральное число называют обнаженным, если оно делится на каждую из своих цифр в отдельности (которые должны быть ненулевыми). Например, 48=4·12=8·6, 672=6·112=7·96=2·336. Введение этого термина объясняют тем, что такие числа раскрывают (обнажают) свои сокровенные тайны. В первом миллионе натуральных чисел содержится 9039 обнаженных чисел. Всего таких чисел бесконечно много, так как любое моноцифровое число является обнаженным.

Первые обнаженные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 15, 22, 24, 33, 36, 44, 48, 55, 66, 77, 88, 99, 111, 112, 115, 122, 124, 126, 128, … . Насколько мне удалось выяснить, этот странный термин ввел некий У. Катагири. Фамилия, распространенная в Японии настолько, что установить, кто он такой не удалось.

Полет фантазии

Процесс отыскания и наименования новых классов чисел среди чисел натуральных, кроме уже рассмотренных, шел сотни лет. Придумано так много разного, что издание с кратким описанием всего открытого и названного должно быть многотомным. Можно только на свой вкус отобрать конечное множество разнообразных определений чисел, и в какой-то момент сказать себе стоп! Попробуем так и сделать.

***

Бесквадратным, или свободным от квадратов, называется число, которое не делится ни на один квадрат, кроме 1. К примеру, 10 – свободное от квадратов, а 18 – нет, так как 18 делится на 9=32. Начало последовательности свободных от квадратов чисел таково: 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 33, 34, 35, 37, 38, 39, … .

Натуральное число n свободно от квадратов тогда и только тогда, когда в разложении этого числа на простые множители ни одно простое число не встречается больше одного раза, то есть все простые множители входят в разложение числа только в первой степени.

***

Гладким числом называется натуральное число, все простые делители которого малы. Поскольку понятие «делители малы» может быть истолковано произвольно, чаще всего гладким числом называют такое, чьи простые делители не превосходят 10 (то есть, фактически равны 2, 3, 5 или 7).

Натуральное число называется M-гладким, если все его простые делители не превосходят M. Исходя из этого определения, можно говорить о 3-гладких, 5-гладких, 7-гладких и т. д. числах. Например, к 3-гладким числам относятся: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, ….Все они в разложении на простые множители имеют только два простых числа 2 и 3 в различных степенях. Число 5000 имеет следующее разложение на множители: 23·54. Поэтому 5000 – это 5-гладкое число, а также 6-гладкое число и так далее, но не 4-гладкое. В основном определении гладкого натурального числа, останавливаются на множителях 2, 3, 5 или 7, следовательно, это определение соответствует 7-гладкому числу. Последовательность таких чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 25, 27, 28, 30, 32, 35, 36, 40, 42, … . То есть, из натурального ряда чисел выбрасываются числа, кратные простым числам начиная от 11 и выше.

***

Полнократное число – натуральное число, которое делится нацело квадратом каждого своего простого делителя. Эквивалентное определение: число, представимое в виде a2·b3, где a и b натуральные числа. Наименование придумано математиком Соломоном Голомбом. Когда мы подходим ближе к нашему времени уже можно четко понять, кто ввел в оборот те или иные числовые определения, история сохраняет имена первооткрывателей. Последовательность полнократных чисел: 1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128, 144, 169, 196, 200, … .

Из определения следует, что квадраты чисел и кубы чисел являются полнократными числами, так как вторым числом в определении может быть единица. Два наименьших последовательных полнократных числа – это 8 и 9. Согласно гипотезе Эрдёша, не существует трёх последовательных полнократных чисел. В связи с понятием полнократных чисел стали рассматривать разложение чисел не только в сумму и произведение других чисел, но ввели в рассмотрение разложение чисел в виде разности двух полнократных чисел. Именно введение разности в рассмотрение – главное значение этого класса чисел. Ведь до сих пор упоминалось сложение, умножение, деление, а о разности даже не заикались. Любое нечетное число представимо в виде разности двух последовательных квадратов: (k+1)2-k2=k2+2k+1-k2=2k+1 – нечетное число. Аналогично в виде разности квадратов представимо любое число кратное четырем: (k+2)2-k2=k2+4k+4-k2=4k+4. Встал вопрос о представлении в виде разности двух полнократных чисел любого числа, кратного двум, но не кратного четырем. Например, 2=33-52. Долго стоял вопрос с разложением числа 6, пока не доказали, что любое число допускает бесконечно много таких представлений. В частности, 6=252·73-4632=214 375-214 369. На русском языке литературы о полнократных числах нет, но спасает то, что в Википедии дается перевод статей на русский и можно почерпнуть информацию.

***

Натуральное число называется необычным, если в его разложении на простые множители самый большой простой множитель строго больше квадратного корня из числа n. Как тяжело писать, когда нельзя употреблять ни редактор формул, ни встроенные символы и приходится использовать только то, что есть на клавиатуре. Вместо одного значка пишешь четыре слова. В определении приходится выходить из множества натуральных чисел и опираться на числа иррациональные, но для полноты охвата прилагательных, применимых к натуральным числам, не хотелось выбрасывать это определение. Все простые числа необычны. Для любого простого p все его кратные меньше p2 необычны. Первые несколько необычных чисел: 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 20, 21, 22, 23, 26, 28, 29, 31, 33, 34, 35, … .

***

Сфеническое натуральное число (от др.-греч. сфена – клин) – число, равное произведению трёх различных простых чисел (так, например, 30=2·3·5; соответственно, число 30 является первым сфеническим). Количество делителей произвольного сфенического числа всегда равно 8. Например, если n=pqr, где p, q и r – разные простые числа, то делителями n будут: 1, p, q, r, pr, qr, pq, pqr Так первое сфеническое число 30 имеет делители: 1, 2, 3, 5, 6, 10, 15 и 30. Сфенические числа образуют последовательность: 30, 42, 66, 70, 78, 102, 105, 110, 114, 130, 138, 154, 165, 170, 174, 182, 186, 190, 195, … . Примером двух последовательных сфенических чисел являются 230 (230=2·5·23) и 231 (231=3·7·11). Примером трёх последовательных сфенических чисел являются 1309 (1309=7·11·17), 1310 (1310=2·5·131) и 1311 (1311=3·19·23). Более чем трёх последовательных сфенических чисел быть не может, поскольку каждое четвёртое натуральное число будет делиться на 4.

***

Радостное число определяется следующим процессом: взяв некоторое натуральное число, замените число суммой квадратов его цифр и повторите процесс до тех пор, пока число либо не будет равно 1 (на чем процесс закончится), либо оно бесконечно крутится в цикле, который не включает 1. Те числа, для которых этот процесс заканчивается в 1, являются радостными числами, а те числа, которые не заканчиваются в 1, будут печальными числами. Происхождение радостных чисел не ясно. Если число радостно, то все члены его последовательности суммирования квадратов цифр радостны; если число печально, все члены последовательности печальны. Например, 19 является радостным, так получается последовательность (+)219: 12+92=82, 82+22=68, 62+82=100, 12+02+02=1. В первой тысяче натуральных чисел есть 143 радостных числа: 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100 … . Радость числа не зависит от перестановки цифр и вставки или удаления любого количества нулей в любом месте числа. Например, радостное число 19 порождает радостные числа: 91, 109, 190, 910 и так далее. Из этого утверждения следует радостный вывод о том, что радостных чисел бесконечно много.

Вариация радостных чисел состоит в том, чтобы, взяв некоторое натуральное число, заменить число суммой кубов его цифр и повторять процесс до тех пор, пока число либо не будет равно 1 (на чем процесс закончится), либо оно бесконечно крутится в цикле, который не включает 1. Например, берем число 1579 и проводим процесс кубирования: 13

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.