Algorithms to Live By: The Computer Science of Human Decisions

When to Park

I find that the three major administrative problems on a campus are sex for the students, athletics for the alumni, and parking for the faculty.

—CLARK KERR, PRESIDENT OF UC BERKELEY, 1958–1967

Another domain where optimal stopping problems abound—and where looking back is also generally ill-advised—is the car. Motorists feature in some of the earliest literature on the secretary problem, and the framework of constant forward motion makes almost every car-trip decision into a stopping problem: the search for a restaurant; the search for a bathroom; and, most acutely for urban drivers, the search for a parking space. Who better to talk to about the ins and outs of parking than the man described by the Los Angeles Times as “the parking rock star,” UCLA Distinguished Professor of Urban Planning Donald Shoup? We drove down from Northern California to visit him, reassuring Shoup that we’d be leaving plenty of time for unexpected traffic. “As for planning on ‘unexpected traffic,’ I think you should plan on expected traffic,” he replied. Shoup is perhaps best known for his book The High Cost of Free Parking, and he has done much to advance the discussion and understanding of what really happens when someone drives to their destination.

We should pity the poor driver. The ideal parking space, as Shoup models it, is one that optimizes a precise balance between the “sticker price” of the space, the time and inconvenience of walking, the time taken seeking the space (which varies wildly with destination, time of day, etc.), and the gas burned in doing so. The equation changes with the number of passengers in the car, who can split the monetary cost of a space but not the search time or the walk. At the same time, the driver needs to consider that the area with the most parking supply may also be the area with the most demand; parking has a game-theoretic component, as you try to outsmart the other drivers on the road while they in turn are trying to outsmart you.* That said, many of the challenges of parking boil down to a single number: the occupancy rate. This is the proportion of all parking spots that are currently occupied. If the occupancy rate is low, it’s easy to find a good parking spot. If it’s high, finding anywhere at all to park is a challenge.

Shoup argues that many of the headaches of parking are consequences of cities adopting policies that result in extremely high occupancy rates. If the cost of parking in a particular location is too low (or—horrors!—nothing at all), then there is a high incentive to park there, rather than to park a little farther away and walk. So everybody tries to park there, but most of them find the spaces are already full, and people end up wasting time and burning fossil fuel as they cruise for a spot.

Shoup’s solution involves installing digital parking meters that are capable of adaptive prices that rise with demand. (This has now been implemented in downtown San Francisco.) The prices are set with a target occupancy rate in mind, and Shoup argues that this rate should be somewhere around 85%—a radical drop from the nearly 100%-packed curbs of most major cities. As he notes, when occupancy goes from 90% to 95%, it accommodates only 5% more cars but doubles the length of everyone’s search.

The key impact that occupancy rate has on parking strategy becomes clear once we recognize that parking is an optimal stopping problem. As you drive along the street, every time you see the occasional empty spot you have to make a decision: should you take this spot, or go a little closer to your destination and try your luck?

Assume you’re on an infinitely long road, with parking spots evenly spaced, and your goal is to minimize the distance you end up walking to your destination. Then the solution is the Look-Then-Leap Rule. The optimally stopping driver should pass up all vacant spots occurring more than a certain distance from the destination and then take the first space that appears thereafter. And the distance at which to switch from looking to leaping depends on the proportion of spots that are likely to be filled—the occupancy rate. The table on the next page gives the distances for some representative proportions.

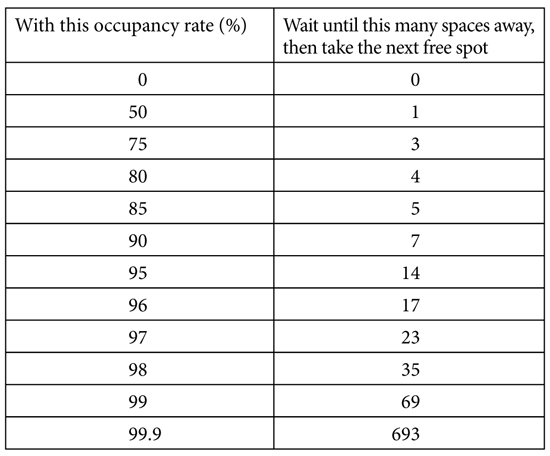
How to optimally find parking.

If this infinite street has a big-city occupancy rate of 99%, with just 1% of spots vacant, then you should take the first spot you see starting at almost 70 spots—more than a quarter mile—from your destination. But if Shoup has his way and occupancy rates drop to just 85%, you don’t need to start seriously looking until you’re half a block away.

Most of us don’t drive on perfectly straight, infinitely long roads. So as with other optimal stopping problems, researchers have considered a variety of tweaks to this basic scenario. For instance, they have studied the optimal parking strategy for cases where the driver can make U-turns, where fewer parking spaces are available the closer one gets to the destination, and where the driver is in competition against rival drivers also heading to the same destination. But whatever the exact parameters of the problem, more vacant spots are always going to make life easier. It’s something of a policy reminder to municipal governments: parking is not as simple as having a resource (spots) and maximizing its utilization (occupancy). Parking is also a process—an optimal stopping problem—and it’s one that consumes attention, time, and fuel, and generates both pollution and congestion. The right policy addresses the whole problem. And, counterintuitively, empty spots on highly desirable blocks can be the sign that things are working correctly.

We asked Shoup if his research allows him to optimize his own commute, through the Los Angeles traffic to his office at UCLA. Does arguably the world’s top expert on parking have some kind of secret weapon?

He does: “I ride my bike.”

When to Quit

In 1997, Forbes magazine identified Boris Berezovsky as the richest man in Russia, with a fortune of roughly $3 billion. Just ten years earlier he had been living on a mathematician’s salary from the USSR Academy of Sciences. He made his billions by drawing on industrial relationships he’d formed through his research to found a company that facilitated interaction between foreign carmakers and the Soviet car manufacturer AvtoVAZ. Berezovky’s company then became a large-scale dealer for the cars that AvtoVAZ produced, using a payment installment scheme to take advantage of hyperinflation in the ruble. Using the funds from this partnership he bought partial ownership of AvtoVAZ itself, then the ORT Television network, and finally the Sibneft oil company. Becoming one of a new class of oligarchs, he participated in politics, supporting Boris Yeltsin’s re-election in 1996 and the choice of Vladimir Putin as his successor in 1999.

But that’s when Berezovsky’s luck turned. Shortly after Putin’s election, Berezovsky publicly objected to proposed constitutional reforms that would expand the power of the president. His continued public criticism of Putin led to the deterioration of their relationship. In October 2000, when Putin was asked about Berezovsky’s criticisms, he replied, “The state has a cudgel in its hands that you use to hit just once, but on the head. We haven’t used this cudgel yet.… The day we get really angry, we won’t hesitate.” Berezovsky left Russia permanently the next month, taking up exile in England, where he continued to criticize Putin’s regime.

How did Berezovsky decide it was time to leave Russia? Is there a way, perhaps, to think mathematically about the advice to “quit while you’re ahead”? Berezovsky in particular might have considered this very question himself, since the topic he had worked on all those years ago as a mathematician was none other than optimal stopping; he authored the first (and, so far, the only) book entirely devoted to the secretary problem.

The problem of quitting while you’re ahead has been analyzed under several different guises, but perhaps the most appropriate to Berezovsky’s case—with apologies to Russian oligarchs—is known as the “burglar problem.” In this problem, a burglar has the opportunity to carry out a sequence of robberies. Each robbery provides some reward, and there’s a chance of getting away with it each time. But if the burglar is caught, he gets arrested and loses all his accumulated gains. What algorithm should he follow to maximize his expected take?

The fact that this problem has a solution is bad news for heist movie screenplays: when the team is trying to lure the old burglar out of retirement for one last job, the canny thief need only crunch the numbers. Moreover, the results are pretty intuitive: the number of robberies you should carry out is roughly equal to the chance you get away, divided by the chance you get caught. If you’re a skilled burglar and have a 90% chance of pulling off each robbery (and a 10% chance of losing it all), then retire after 90/10 = 9 robberies. A ham-fisted amateur with a 50/50 chance of success? The first time you have nothing to lose, but don’t push your luck more than once.

Despite his expertise in optimal stopping, Berezovsky’s story ends sadly. He died in March 2013, found by a bodyguard in the locked bathroom of his house in Berkshire with a ligature around his neck. The official conclusion of a postmortem examination was that he had committed suicide, hanging himself after losing much of his wealth through a series of high-profile legal cases involving his enemies in Russia. Perhaps he should have stopped sooner—amassing just a few tens of millions of dollars, say, and not getting into politics. But, alas, that was not his style. One of his mathematician friends, Leonid Boguslavsky, told a story about Berezovsky from when they were both young researchers: on a water-skiing trip to a lake near Moscow, the boat they had planned to use broke down. Here’s how David Hoffman tells it in his book The Oligarchs:

While their friends went to the beach and lit a bonfire, Boguslavsky and Berezovsky headed to the dock to try to repair the motor.… Three hours later, they had taken apart and reassembled the motor. It was still dead. They had missed most of the party, yet Berezovsky insisted they had to keep trying. “We tried this and that,” Boguslavsky recalled. Berezovsky would not give up.

Surprisingly, not giving up—ever—also makes an appearance in the optimal stopping literature. It might not seem like it from the wide range of problems we have discussed, but there are sequential decision-making problems for which there is no optimal stopping rule. A simple example is the game of “triple or nothing.” Imagine you have $1.00, and can play the following game as many times as you want: bet all your money, and have a 50% chance of receiving triple the amount and a 50% chance of losing your entire stake. How many times should you play? Despite its simplicity, there is no optimal stopping rule for this problem, since each time you play, your average gains are a little higher. Starting with $1.00, you will get $3.00 half the time and $0.00 half the time, so on average you expect to end the first round with $1.50 in your pocket. Then, if you were lucky in the first round, the two possibilities from the $3.00 you’ve just won are $9.00 and $0.00—for an average return of $4.50 from the second bet. The math shows that you should always keep playing. But if you follow this strategy, you will eventually lose everything. Some problems are better avoided than solved.

Always Be Stopping

I expect to pass through this world but once. Any good therefore that I can do, or any kindness that I can show to any fellow creature, let me do it now. Let me not defer or neglect it, for I shall not pass this way again.

—STEPHEN GRELLET

Spend the afternoon. You can’t take it with you.

—ANNIE DILLARD

We’ve looked at specific cases of people confronting stopping problems in their lives, and it’s clear that most of us encounter these kinds of problems, in one form or another, daily. Whether it involves secretaries, fiancé(e)s, or apartments, life is full of optimal stopping. So the irresistible question is whether—by evolution or education or intuition—we actually do follow the best strategies.

At first glance, the answer is no. About a dozen studies have produced the same result: people tend to stop early, leaving better applicants unseen. To get a better sense for these findings, we talked to UC Riverside’s Amnon Rapoport, who has been running optimal stopping experiments in the laboratory for more than forty years.

The study that most closely follows the classical secretary problem was run in the 1990s by Rapoport and his collaborator Darryl Seale. In this study people went through numerous repetitions of the secretary problem, with either 40 or 80 applicants each time. The overall rate at which people found the best possible applicant was pretty good: about 31%, not far from the optimal 37%. Most people acted in a way that was consistent with the Look-Then-Leap Rule, but they leapt sooner than they should have more than four-fifths of the time.

Rapoport told us that he keeps this in mind when solving optimal stopping problems in his own life. In searching for an apartment, for instance, he fights his own urge to commit quickly. “Despite the fact that by nature I am very impatient and I want to take the first apartment, I try to control myself!”

But that impatience suggests another consideration that isn’t taken into account in the classical secretary problem: the role of time. After all, the whole time you’re searching for a secretary, you don’t have a secretary. What’s more, you’re spending the day conducting interviews instead of getting your own work done.

This type of cost offers a potential explanation for why people stop early when solving a secretary problem in the lab. Seale and Rapoport showed that if the cost of seeing each applicant is imagined to be, for instance, 1% of the value of finding the best secretary, then the optimal strategy would perfectly align with where people actually switched from looking to leaping in their experiment.

The mystery is that in Seale and Rapoport’s study, there wasn’t a cost for search. So why might people in the laboratory be acting like there was one?

Because for people there’s always a time cost. It doesn’t come from the design of the experiment. It comes from people’s lives.

The “endogenous” time costs of searching, which aren’t usually captured by optimal stopping models, might thus provide an explanation for why human decision-making routinely diverges from the prescriptions of those models. As optimal stopping researcher Neil Bearden puts it, “After searching for a while, we humans just tend to get bored. It’s not irrational to get bored, but it’s hard to model that rigorously.”

But this doesn’t make optimal stopping problems less important; it actually makes them more important, because the flow of time turns all decision-making into optimal stopping.

“The theory of optimal stopping is concerned with the problem of choosing a time to take a given action,” opens the definitive textbook on optimal stopping, and it’s hard to think of a more concise description of the human condition. We decide the right time to buy stocks and the right time to sell them, sure; but also the right time to open the bottle of wine we’ve been keeping around for a special occasion, the right moment to interrupt someone, the right moment to kiss them.

Viewed this way, the secretary problem’s most fundamental yet most unbelievable assumption—its strict seriality, its inexorable one-way march—is revealed to be the nature of time itself. As such, the explicit premise of the optimal stopping problem is the implicit premise of what it is to be alive. It’s this that forces us to decide based on possibilities we’ve not yet seen, this that forces us to embrace high rates of failure even when acting optimally. No choice recurs. We may get similar choices again, but never that exact one. Hesitation—inaction—is just as irrevocable as action. What the motorist, locked on the one-way road, is to space, we are to the fourth dimension: we truly pass this way but once.

Intuitively, we think that rational decision-making means exhaustively enumerating our options, weighing each one carefully, and then selecting the best. But in practice, when the clock—or the ticker—is ticking, few aspects of decision-making (or of thinking more generally) are as important as one: when to stop.

*We use boldface to indicate the algorithms that appear throughout the book.

*With this strategy we have a 33% risk of dismissing the best applicant and a 16% risk of never meeting her. To elaborate, there are exactly six possible orderings of the three applicants: 1-2-3, 1-3-2, 2-1-3, 2-3-1, 3-1-2, and 3-2-1. The strategy of looking at the first applicant and then leaping for whoever surpasses her will succeed in three of the six cases (2-1-3, 2-3-1, 3-1-2) and will fail in the other three—twice by being overly choosy (1-2-3, 1-3-2) and once by not being choosy enough (3-2-1).

*Just a hair under 37%, actually. To be precise, the mathematically optimal proportion of applicants to look at is 1/e—the same mathematical constant e, equivalent to 2.71828…, that shows up in calculations of compound interest. But you don’t need to worry about knowing e to twelve decimal places: anything between 35% and 40% provides a success rate extremely close to the maximum. For more of the mathematical details, see the notes at the end of the book.

*More on the computational perils of game theory in chapter 11.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.