It All Adds Up: The Story of People and Mathematics

Copyright

William Collins

An imprint of HarperCollinsPublishers

1 London Bridge Street

London SE1 9GF

www.WilliamCollinsBooks.com

This eBook first published in Great Britain by William Collins in 2018

First published in France by Flammarion, as Le grand romans des maths in 2016

Copyright © Mickaël Launay 2016

Translation copyright © Stephen S Wilson 2018

Drawing here by Maurice Bourlon; Image here © IRSNB, Thierry HubinMap here in the public domain, courtesy of Bibliothèque nationale de France, GE BB-565 (A7,10); Image here from Wikimedia Commons; Image here by Stefan Zachow.

Mickaël Launay asserts the moral right to be identified as the author of this work

Stephen S Wilson asserts the moral right to be identified as the translator of this work in accordance with the Copyright, Designs and Patents Act 1988

A catalogue record for this book is available from the British Library

All rights reserved under International and Pan-American Copyright Conventions. By payment of the required fees, you have been granted the non-exclusive, non-transferable right to access and read the text of this e-book on-screen. No part of this text may be reproduced, transmitted, down-loaded, decompiled, reverse engineered, or stored in or introduced into any information storage and retrieval system, in any form or by any means, whether electronic or mechanical, now known or hereinafter invented, without the express written permission of HarperCollins

Source ISBN: 9780008283933

Ebook Edition © October 2018 ISBN: 9780008283957

Version: 2018-11-08

Contents

Cover

Title Page

Copyright

Foreword

1. Mathematicians without knowing it

2. And then there were numbers

3. Let no one ignorant of geometry enter

4. The age of theorems

5. A little method

6. Π in the sky

7. Nothing and less than nothing

8. The power of triangles

9. Into the unknown

10. In sequence

11. Imaginary worlds

12. A language for mathematics

13. The world’s alphabet

14. The infinitely small

15. Measuring the future

16. The coming of machines

17. Maths to come

Epilogue

To go further

Footnotes

Bibliography

Index

About the Author

About the Publisher

FOREWORD

‘Oh, I’ve never been much good at maths myself!’

I’m getting a little blasé. This must be at least the tenth time I’ve heard that remark today.

But this lady has been here at my stall for a good fifteen minutes, standing with a group of other visitors, listening attentively while I describe various geometrical curiosities. That’s how the conversation started.

‘But what do you do for a living?’ she asked me.

‘I’m a mathematician.’

‘Oh, I’ve never been much good at maths myself!’

‘Really? But you seemed to be interested in what I was just talking about.’

‘Yes … but that’s not really maths … that was understandable.’

I hadn’t heard that one before. Is mathematics, by definition, a discipline that can’t be understood?

It’s the beginning of August, in the Cours Félix Faure in La Flotte-en-Ré, France. In this small summer market, I have a pop-up – there is henna tattooing and afro braids to my right, a mobile-phone accessory stall to my left, and a display of jewels and trinkets of all kinds opposite me. I’ve set up my maths stand in the middle of all this. Holidaymakers stroll peacefully by in the cool of the evening. I particularly like doing maths in unusual places. Where people aren’t expecting it. Where they are not on their guard …

‘Can’t wait to tell my parents I did some maths during the holidays!’ This from a secondary school pupil as he walks past my stall on his way back from the beach.

It’s true – I do catch them slightly unawares. But sometimes you’ve got to do what you’ve got to do. This is one of my favourite moments: observing the expression on the faces of people who thought that they had fallen out with maths for good at the instant when I tell them that they have just been doing maths for fifteen minutes. And my stall is always crowded! I present origami, magic tricks, games, riddles … there’s something for everyone.

No matter how much this amuses me, on balance I find it upsetting. How has it come about that we need to hide from people the fact that they are doing maths before they can take some pleasure in it? Why is the word so frightening? One thing is certain: had I put up a sign above my table proclaiming ‘Mathematics’ as visibly as ‘Jewels and necklaces’, ‘Phones’ or ‘Tattooing’ on the stalls around me, I would not have had a quarter of the same success. People would not have stopped. Perhaps they would even have turned away and averted their gaze.

All the same, the curiosity is there. I observe this every day. Mathematics is scary, yet even more, it is fascinating. Some may not like it, but would like to like it, or at least to be able to peep at will into its murky mysteries. Many think it is inaccessible. But this is not true. It is perfectly possible to love music without being a musician, or to like to share a nice meal without being a great cook. Then why should you have to be a mathematician, or someone exceptionally clever, in order to be open to hearing about mathematics and to enjoy having your imagination tickled by algebra or geometry? It is not necessary to delve into the technical details in order to understand the great ideas and to be able to marvel at them.

Since time out of mind, innumerable artists, creative spirits, inventors, artisans, simple dreamers, or the purely curious, have done maths without being aware of the fact: mathematicians despite themselves. They were the first to ask questions, the first to undertake research, the first to brainstorm. If we want to understand the whys and wherefores of mathematics, we have to set out on their trail, since it all began with them.

The time has come to embark on a journey. Please allow me the space of these few pages to carry you with me into the twists and turns of one of the most fascinating and most astonishing disciplines ever practised by humankind. Let us set off to meet those who have created its story through unexpected discoveries and fabulous ideas.

Let us set out on a big adventure and see how it all adds up.

1

MATHEMATICIANS WITHOUT KNOWING IT

Back in Paris, it is at the Louvre Museum, in the heart of the French capital, that I decide to begin our investigation. Am I going to do maths in the Louvre? That may seem incongruous. Nowadays the former royal residence, converted into a museum, seems to be the domain of painters, sculptors, archaeologists and historians rather than of mathematicians. However, it is here that we can now hark back to the first traces of those same mathematicians.

From the moment I arrive, the appearance of the great glass pyramid that has pride of place in the centre of the Napoleon Courtyard is already an invitation to geometry. But today I have an appointment with a much more ancient era. As I enter the museum the time machine wakes up. I pass by the Kings of France and travel back through the Renaissance and the Middle Ages before arriving in Antiquity. The rooms spool by, I come across a few Roman statues, Greek vases, Egyptian sarcophagi. Still a little further to go. Now I’m entering prehistory, and as I speed through the centuries I gradually need to forget everything: numbers, geometry, writing. In the beginning, no one knew anything. No one even knew that there was something to know.

The first stop is in Mesopotamia. We have travelled back ten thousand years.

Come to think of it, I could have gone back even further. I could have flown back another one-and-a-half million years, to the heart of the Palaeolithic, the Old Stone Age. Fire has not yet been tamed and Homo sapiens is only a distant prospect. Homo erectus reigns in Asia, and Homo ergaster in Africa, perhaps with other cousins as yet undiscovered. This is the age of flake stone tools. The biface has arrived.

Flint knappers are at work in a corner of the encampment. One of them picks up a virgin piece of flint, which is still just as it was when he chose it a few hours earlier. He sits down on the bare earth, places the stone on the ground, and holds it steady with one hand, while with the other hand he strikes its edge with a heavy stone. A first flake breaks off. He examines the result, turns his flint over and strikes it a second time on the other side. The first two flakes that have broken off in this way, opposite one another, leave a sharp edge on the flint. It only remains to repeat the operation along the whole of the contour. In some places the flint is too thick or too wide, and larger pieces have to be removed in order to give the final object the shape desired.

For the shape of the biface is not left to chance or to the whim of the moment. It is designed, worked, and transmitted from generation to generation. We find various different models, according to the period and to where they were produced. Some are shaped like a drop of water with a prominent point, other more rounded ones are egg-shaped, while others are more like an isosceles triangle with very slightly curved sides.

Biface from the Lower Palaeolithic

But they all have one thing in common: an axis of symmetry. Could there be a practical aspect to this geometry, or was it simply an aesthetic intention that drove our ancestors to adopt these shapes? The flint knapper’s blows had to be premeditated. He had to think about the shape before creating it, to construct an abstract image in his own mind of the object to be crafted. In other words, he had to do some mathematics.

When he finished the piece, the knapper inspected his new tool, held it up to the light at arm’s length to better scrutinize the contour, and altered a few cutting edges with two or three more sharp taps before he was finally satisfied. How did he feel at that moment? Did he already experience the tremendous exaltation of scientific creativity: of having been able to grasp and shape the outside world, through an abstract idea? It doesn’t matter; the finest hours of abstraction had not yet arrived. This is a time of pragmatism. The biface would be used to cut wood, to cut up meat, to pierce animal hides and to dig holes in the ground.

But no, we shall not travel so far back. Let us allow these ancient times and these few random interpretations to rest in peace, and let us return to what will become the true point of departure for our adventure: the Mesopotamian region in the eighth millennium BC.

All along the Fertile Crescent, in a zone that roughly corresponds to the area now known as Iraq, the Neolithic revolution was under way. People had been settling there for some time. In the northern plateaux, sedentarization was a success story. The region was the laboratory for all the very latest innovations. The mudbrick houses formed the first villages, and the bravest builders were even at that time adding a storey. Agriculture was a state-of-the-art technology. The temperate climate meant that the land could be cultivated without artificial irrigation. Animals and plants were gradually being domesticated. Pottery was on the verge of emerging.

Speaking of which, let’s talk about pottery. For while many testimonies to these periods have disappeared, irreparably lost in the mists of time, nevertheless archaeologists continue to gather thousands of artefacts: pots, vases, jars, plates, bowls, etc. The display cabinets around me are full of them. The earliest date from 9,000 years ago, and from room to room, like the pebbles of Hop-o’-My-Thumb, they guide us through the centuries. They come in all shapes and sizes and are variously decorated, sculpted, painted or engraved. Some have feet, others have handles. Some are intact, cracked, broken, or have been reconstituted. In some cases, only a few sparse fragments remain.

Ceramics was the first art to use fire – well before bronze, iron or glass. Artisan potters were able to use clay, that paste of malleable rock and soil material which can be harvested in abundance in these humid regions, to fashion objects as they wished. When they were satisfied with the shape, they had only to let the objects dry for a few days, before cooking them in a great fire so that they solidified. This technique had already been known for a long time. Twenty thousand years earlier people were already producing small statuettes. But the idea of producing utensils out of clay had only arisen recently with sedentarization. The new way of life required a means of storage, so pots were produced in bulk.

These earthenware receptacles rapidly came to be indispensable to everyday life and also necessary for the collective organization of the village. If there was going to be washing up to do, it might as well be beautiful – soon, pots were being decorated. Here again, there were several approaches. Some potters imprinted their patterns in the clay while it was still fresh by using a shell or a twig, before baking the pot. Some did the baking first before engraving their decorations using stone tools. Others preferred to paint on the surface with the help of natural pigments.

As I pass through the rooms of the Near Eastern Antiquities section, I am struck by the richness of the geometric patterns conceived by the Mesopotamians. Just as it was for our flint knapper’s biface, some symmetries are so ingenious that they must have been very thoughtfully designed in advance. The friezes running round the rims of these vases pique my interest.

The friezes are decorated bands with a single pattern repeated round the whole circumference of the pot. The most common ones include triangular sawtooth designs. There are also friezes showing two intertwined strings. Then there are friezes with angled rectangles, friezes with square indentations, friezes with pointed lozenges, with hatched triangles, with interlocking circles, and so on.

When one moves from one region to another or from one period to the next, trends can be seen. Certain patterns are very popular. They are reworked, transformed, improved in multiple variants. Then, several years later, they are essentially abandoned, replaced by other designs that are fashionable at the time.

My mathematician’s eyes light up as I spot symmetries, rotations and translations. Then in my mind I begin to sort and arrange all this. Several theorems from my undergraduate days come back to me. What I need is the classification of geometric transformations. I take out a notebook and a pencil and begin to scribble.

First, there are rotations. Appropriately, in front of me there is a frieze consisting of S-shaped patterns interlocking one after the other. I tilt my head to make sure I’m right. Yes, there’s no doubt, this one is invariant under a half-turn: if I were to take the earthenware jar and turn it upside down, the frieze would still look exactly the same.

Then there are symmetries. There are several types of these. I am gradually filling in my list and a treasure hunt begins. For each geometric transformation I look for the corresponding frieze. Moving from room to room, I retrace my steps. Some pieces are damaged, so I squint to try to reconstitute the patterns that ran across this clay thousands of years ago. When I find a new pattern, I tick it off. I look at the dates to try to reconstitute the chronology in which the patterns appeared.

How many patterns should I find in total? After a little thought, I finally manage to put my finger on this famous theorem. There are, in sum total, seven categories of friezes. Seven different groups of geometric transformations that can leave them invariant. Not one more, not one less.

That is not something the Mesopotamians knew. And with good reason, as the first formalization of the theory in question only began in the Renaissance. However, without knowing it, and without pretending to be doing anything other than decorating their pottery with harmonious and original designs, these prehistoric potters were actually undertaking the very first reasoning in a fantastic discipline, that would focus the efforts of a whole community of mathematicians thousands of years later.

Looking over my notes, I see almost all the patterns. Almost? I’m still missing one of the seven friezes. This doesn’t surprise me a lot, as this frieze is clearly the most complicated one on the list. I am looking for a frieze that, if you flip it over horizontally, will have the same appearance but shifted by half a pattern length. Today, we call this a glide symmetry. This would have been a real challenge for Mesopotamians.

However, I still have not visited all the rooms, so I’m not losing hope – the hunt is still on. I observe the smallest detail, the least indication. Examples of the other six categories, those I have already observed, are piling up. In my notebook, the dates, sketches and other scribbles are getting muddled. But still no sign of the mysterious seventh frieze.

All at once, a rush of adrenalin. Behind this glass panel I have just spotted a piece that looks in a bit of a sorry state. A simple fragment. From top to bottom you can clearly make out four partial friezes, one above the other, and one of these has caught my eye. The third one down – it consists of what look like fragments of inclined interlocking rectangles. My eyes are blinking. I’m peering attentively, sketching the pattern quickly in my notebook, as though I’m afraid it will vanish before my eyes. It has the right geometry. This really is the glide symmetry. The seventh frieze is unmasked.

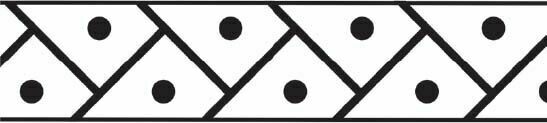
The caption next to it says: Fragment of beaker with horizontal décor of bands and pointed lozenges. Middle of the fifth millennium BC.

I insert it mentally in my chronology. Mid-fifth millennium BC. We are still in prehistory. More than a thousand years before the invention of writing – without knowing it – the Mesopotamian potters had listed all the cases of a theorem that would only be stated and proved 6,000 years later.

A few rooms further, I come across an earthenware jar with three handles, which also falls into the seventh category: even though the pattern has become a spiral, the geometric structure remains the same. A little further on again, there is another one. I would like to continue, but suddenly the décor changes and I have arrived at the end of the Near Eastern collection. If I continue, I will reach Greece. I cast a last glance at my notes; the friezes with glide symmetry can be counted on the fingers of one hand. I had a stroke of luck.

HOW TO RECOGNIZE THE SEVEN CATEGORIES OF FRIEZES

The first category is that of friezes that have no particular geometric property, and in which a simple pattern is repeated without symmetries or centres of rotation. This is, in particular, the case for friezes that are not based on geometric figures but on figurative drawings, for instance of animals.

The second category consists of friezes in which the horizontal line dividing the figure in two is an axis of symmetry.

The third category comprises friezes that have a vertical axis of symmetry. Since a frieze consists of a pattern that is repeated horizontally, the vertical axes of symmetry are also repeated.

The fourth category is that of friezes that are invariant under a rotation by a half-turn. Whether you look at these friezes from above or below you will always see the same thing.

The fifth category is that of glide symmetries. This notable category was the last one I discovered while passing through Mesopotamia. If you reflect such a frieze about a horizontal axis of symmetry (as per the second category) the frieze obtained is similar, but translated by half a pattern length.

The sixth and seventh categories do not correspond to new geometric transformations, but combine several of the properties encountered in the previous categories. Thus, the friezes of the sixth category are those that have a horizontal symmetry, a vertical symmetry and a centre of rotation by a half-turn, all at the same time.

Finally, the seventh category consists of friezes that have a vertical symmetry, a centre of rotation and a glide symmetry.

Note that these categories only relate to the geometric structure of the friezes and do not exclude possible variations in the pattern designs. Thus, while the following friezes are all different, they all belong to the seventh category.

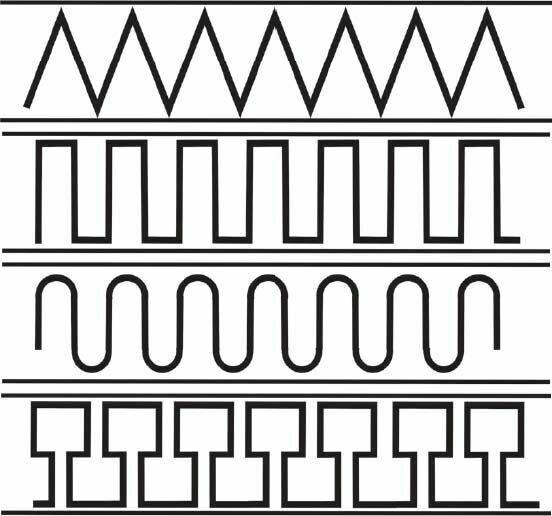
Therefore, all the friezes that you can possibly imagine belong to one of these seven categories. Any other combination is geometrically impossible. Curiously, the last two categories are the most common. It is spontaneously easier to draw figures with a lot of symmetries than figures that have only a few.

Bursting with pride following my successes with the Mesopotamians, I am back the very next day, ready to take ancient Greece by storm. I have barely arrived and already I am overwhelmed with choice. The hunt for friezes here is child’s play. After just a few steps, a few display cases and a few black amphoras decorated with red figures, I have already found my list of seven friezes again.

Faced with such an abundance of riches, I quickly decide not to record my statistics as I had done in Mesopotamia. I am amazed by the creativity of the artists. Ever more complex and ingenious new patterns come into view. I have to pause several times and concentrate hard in order to unravel in my mind all the intertwined visions that are swirling around me.