
Полная версия
Biblical Chronology

Biblical Chronology
Valeriy Sterkh
Translator Evgeniy Terekhin
Translator Valeriy Sterkh
© Valeriy Sterkh, 2022
© Evgeniy Terekhin, translation, 2022
© Valeriy Sterkh, translation, 2022
ISBN 978-5-4493-3768-9
Created with Ridero smart publishing system
Foreword
Throughout centuries, numerous attempts have been made to recreate biblical dates and chronology. Yet there is still no consensus in this regard – for various reasons. This book briefly discusses the problems of the Old Testament chronology and provides a more detailed timeline of the era of Jesus Christ. The main flaw of the various existing versions of the New Testament chronology is that they do not completely align with the Four Gospels and the historical evidence. To solve this problem, we had to re-create all the chronological calculations to see how well they correlate with each other. The results was highly satisfactory. The calculations and explanations presented here are simple, so anyone can verify them. In conclusion, the book addresses some of the issues related to reforming the Church calendar and suggests possible solutions.
Section 1. The basics of chronology
Calendar systems
Chronology is always based on a certain calendar. And calendars are based on solar and lunar cycles. This simple truth we find in the very first pages of the Bible:
“And God said, Let there be lights in the firmament of the heaven to divide the day from the night; and let them be for signs, and for seasons, and for days, and years: And let them be for lights in the firmament of the heaven to give light upon the earth: and it was so. And God made two great lights; the greater light to rule the day, and the lesser light to rule the night: he made the stars also. And God set them in the firmament of the heaven to give light upon the earth, And to rule over the day and over the night, and to divide the light from the darkness: and God saw that it was good. And the evening and the morning were the fourth day” (Gen 1:14—19).
There are three types of calendar systems: solar, lunar and lunisolar. These systems have engendered many types of calendars. Below we will consider only those that are necessary for recreating the biblical chronology.
The Julian calendar
In 46 BNE (Before New Era), the Roman calendar was reformed by Gaius Julius Caesar (100 – 44 BNE). This solar calendar was based on the average duration of the year equal to 365.25 days. Since the calendar year can only consist of a whole number of days, it was agreed that the standard year would consist of 365 days, and every fourth (leap year) would be 366 days. The calendar was introduced on January 1, 45 BNE – on a new moon. In the days of Octavian Augustus (63 BNE – 12 NE), the Julian calendar underwent slight modifications and since then was used in a fixed form in many countries, until it was replaced by the Gregorian calendar.
The duration of the months in the Julian calendar is as follows: 1. January – 31 days, 2. February – 28 days (leap year – 29 days), March – 31 days, 4. April – 30 days, 5. May – 31 days, 6. June – 30 days, 7. July – 31 days, 8. August – 31 days, 9. September – 30 days, 10. October – 31 days, 11. November – 30 days, 12. December – 31 days.
In the age of Jesus Christ, the Julian calendar was in wide use. Later this calendar was adopted by the Christian Church. In light of this, and also because of its simplicity and convenience, we will primarily use the Julian calendar dates in making our calculations.
Counting days according to the Roman calendar
The ancient Romans used a special system for counting days in a given month. The first day of the month was called “calends” (calendae or kalendae). The middle day of the month was called “idus”. The ninth day before idus was called “nona” (nonae), counting inclusively. Initially, calends, nones, and idus roughly coincided with the new moon, the first quarter of the moon, and the full moon, respectively. With time, however, this correlation was broken. Yet the traditional naming of days in this way remained intact for a long time. The day before calends, nones, and idus was called “eve” (pridie). The remaining days were numbered in the reverse order: so many days before nones, idus, or calends. In the leap year, an additional 366th day was inserted between February 23 and 24. It was called “bis sextum kal. Mart” (“twice sixth before the March calends”). The year was called “annus bissextus”, from which the term “bissextile year” or “leap year” is derived.
This system of numbering days was used for a long time, even after the reform of the calendar by Julius Ceasar.

Reference points
We have already touched upon the NE designation in relation to the numbering of years (it means “from our era” or “from the new era”). Historically, this reference point was called “the year of Our Lord” (Anno Domini or AD). The origin of this designation is ascribed to the monk Dionysius Exiguus (c. 470 – c. 544 NE). Later it became obvious that Dionysius had made a mistake in his calculations, but the tradition of counting years from this reference point was not discontinued. We will also stay within this framework as we proceed in our study, and all the dates that you will see in this book will correlate with this system, unless otherwise stated. For more information about the era of Dionysius Exiguus see Section 3. In the meantime, let us note that all the years following this reference point are designated as NE (AD), and the years preceding it are designated as BNE (BC). In other words, the 1st year NE is preceded by the 1st year BNE. It is normal for this type of count (historical or chronological), where the “zero year” is absent. But since such a way of counting is not always convenient, the so-called “astronomical year system” was introduced, where the 1st year BNE corresponds to the zero year, the 2nd year BNE corresponds to the -1 NE, and so on. This method is better suited for calculations in general.
Before the introduction of the Anno Domini (AD) designation, there were other reference points too. There were chronologies based on the year of the Olympic Games, as well as on the year since the foundation of Rome, since the beginning of the emperor’s reign, and since “the foundation of the world” (several versions), etc.
Counting days since the foundation of Rome
Before the Era of Dionysius (AD), chronology was often based on the “since the foundation of Rome” reference point. It was called “ab urbe condita” (“since the foundation of the city”). This reference was popularized by Mark Terentius Varro (116 – 27 BNE), and it corresponded to April 21, 753 BNE.
To convert a year “since the foundation of Rome” (a.u.c.) into the year NE, the following formula was used:
R = auc – 753
For example, 750 a.u.c. corresponds to -3 NE according to the astronomical system, or 4 BNE.
Counting days based on Olympic years
One other way of time keeping in the ancient world was to count years relative to the Olympic Games. Since the Olympiads were held once every four years, the years were designated as “the first” (second, third, fourth) since the year of a specific Olympiad. The reference point for the first year of the first Olympiad corresponds to July 1, 776 BNE.
To convert a year based on the Olympiad into the NE system, the following formula was used:
R = [(Ol – 1) * 4 + (t – 1)] – 775,
where “Ol” is the number of the Olympic Games, and “t” is the number of the year since the Olympiad.
For example, the 4th year of the 48th Olympiad (Ol. 48.4) converts into -584 NE, or 585 BNE. This was the year of the eclipse of Thales (see Pliny the Elder. Natural History, 2,12).
The Egyptian calendar
The Roman calendar was a modification of the Egyptian calendar. A number of ancient writers (mainly from the church of Alexandria) continued to use the Egyptian calendar even after the Julian calendar was in wide use.
The Egyptian calendar consisted of 12 months, 30 days each. The Greek names of the months are as follows: 1. Thoth, 2. Phaophi, 3. Athyr, 4. Choiak, 5. Tybi, 6. Mechir, 7. Phamenoth, 8. Pharmuthi, 9. Pachon, 10. Payni, 11. Epiphi, 12. Mesori.
At the end of the year, five more days were added, which were called in Greek “epagomen”. So, there were the total of 365 days in the Egyptian calendar year.
Claudius Ptolemy (c. 100 – c. 170 NE), the ancient Greek scholar, is credited with tracing the beginnings of the Egyptian calendar down to the enthronement of the Babylonian king Nabonassar. The reference point of the Nabonassar era (1 Toth) corresponds to February 26, 747 BNE.
The exact alignment of eras
Based on the above, the following equasion can be suggested:
1 NE = 754 a.u.c. = Ol. 195.1 = 748 Nabonassar
As you may have noticed, the formulas for converting dates between different chronologies are approximate; they do not account for the differences between the times of change from one year to the next for the specified eras. Using these formulas, the calculations can sometimes be off by a whole year. To avoid it, it is necessary to take into account the exact date of an event (day and month), so you can make adjustments in the process of calculations.
The Egyptian calendar is even more challenging. At first, it doesn’t seem very complicated, because we know that January 1 of the year 1 NE corresponds to Tybi 12, 748, of the Nabonassar era. However, the Egyptian year consists of 365 days, whereas the Julian calendar year is 365.25 days. That is why every 4 years these two calendars get adjusted against each other by one day. The process of converting Egyptian calendar dates into the corresponding Julian calendar dates will be explained in later chapters.
Since the foundation of the world
In the first ages of Christianity, attempts were made to count years since the foundation of the world, or from Adam. Annalists made their calculations based on the Old Testament data but came up with varying results, for which reason this type of chronology was not widely accepted. Partcularly, the scholars disagreed on how much time had passed from the Babylonean exile of the Jews (6th century BNE) up to the New Testament events, because the Bible does not cover this chronological period. So they had to use external chronicles, which were not always reliable. Only several versions of the eras “since the foundation of the world” have any historical significance:
The Antioch era (reference point: September 1, 5500 BNE, Friday). Developed by the bishop Theophilus of Antioch, circa 180. Some sources give other reference points: 5969, 5515, or 5507 BNE. But they were not used in the chronicles.
The era of Hippolytus of Rome (reference point: 5503 BNE). Appeared around the year 200.
The era of Sextus Julius Africanus (reference point 5502 BNE). Appeared around 220; used in “Chronography”.
Theophilus, Hippolytus, Julius and other ancient writers believed that the period of time between Adam and the New Testament (Jesus Christ) was 5500 years. The basis for this belief was the biblical account of the creation of man in the middle of the 6th day (Gen 1:24—31), and also the words of Scripture: “For a thousand years in thy sight are but as yesterday when it is past” (Ps 90:4 [Ps 89:5 rus]), and: “But, beloved, be not ignorant of this one thing, that one day is with the Lord as a thousand years, and a thousand years as one day” (2 Pet 3:8). There were often discrepancies in these eras as to the date of Christ’s birth. Some scholars believed that 5500 years was an approximate marker – the Bible does not conclusively say that Adam was created exactly in the middle of the 6th day. So deviations from this date were allowed. There were also some who counted 5500 years from Adam’s fall, not from the foundation of the world. Other denied any correlation between the millenia on the timeline of history and the number of creation days.
The Old Byzantine era (reference point: 5504 BNE). Used in Byzantium until the 4th century. Also used in the ancient Rus and Bulgaria.
The Byzantine era (reference point: September 1, 5509 BNE, Saturday). Introduced under the Emperor Constantius in the 4th century. It was used in Byzantinum up to the 6th century, and in Russia starting with 15th century. The reference point was shifted so that the indiction numbers would be easier to find. For the year 5509 BNE, the indiction numbers equal one. For the succeeding years, the indiction numbers are the remainder of the division of the Byzantine date by 28, 19, and 15. The remainder value equalled to the circle of the Sun, the Moon and the indiction, respectively.
The era of Panodorus of Alexandria (reference point August 29, 5493 BNE, Tuesday). Introduced by Panodorus of Alexandria around the year 400.
The era of Annianus (reference point: March 25, 5492 BNE, Sunday). introduced by Annianus of Alexandria in the beginning of the 5th century.
The era of Alexandria (reference point: September 1, 5493 BNE, Friday). It is a modification of the eras of Panodorus and Annianus. Used by the Byzantine historians.
The March Byzantine era (reference point: March 1, 5508 BNE, Friday). Used in Byzantium starting with the 6th century, and in the ancient Rus up until the 12th century.
The Ultramarch Byzantine era (reference point: March 1, 5509 BNE, Thursday). Used in the medieval Rus, between the 12th and 15th centuries.
The eras “since the foundation of the world” were so numerous that annalists often gave their dates in several chronological systems – to avoid confusion.
The Jewish calendar
We know very little about the original Jewish calendar. Four months of the ancient calendar are mentioned in the Old Testament: Aviv [Abib] (the first month, the month of ears of corn) [Ex 13:4], Zif (the second month, month of blossoms) [1 Kings 6:1], Ethanim (the seventh month, the month of strong winds) [1 Kings 8:2], Bul (the eighth month, the month of the harvest) [1 Kings 6:38].
While in Babylonean captivity, the Jews adopted the lunisolar calendar of their captors. It is easy to verify by comparing the names of the ancient Babylon months with the contemporary Jewish calendar.
The names of the ancient Babylon months: 1. Nisannu, 2. Ayyaru, 3. Simanu, 4. Duuzu, 5. Abu, 6. Ululu, 7. Tasritu, 8. Arahsamna, 9. Kislimu, 10. Tebetu, 11. Sabatu, 12. Addaru.
The names of months in the late Jewish calendar: 1. Nisan (former Aviv), 2. Iyyar (former Zif), 3. Siwan, 4. Tammuz, 5. Ab, 6. Elul, 7. Tisri (former Ethanim), 8. Marheswan (former Bul), 9. Kislew, 10. Tebet, 11. Sebat, 12. Adar.
In the ancient Jewish world, the appearance of the first crescent in the evening sky, which was called “neomenia”, marked the beginning of the month. The moment of neomenia was simply observed, and then the beginning of the new month was announced. So, there were 29 or 30 days in a month. The standard year had 12 months. But since the tropical (solar) year consists of 12.36826 synodic (lunar) months, the inaccuracy added up over time and had to be eliminated by adding an extra month. Whether there was a need for the extra month was determined based on the conditions of the grain crops and the age of the sacrificial animals – after all, the Passover law had to be observed: “In the fourteenth day of the first month [Nisan (Aviv)] at even is the LORD’S passover… Ye shall bring a sheaf of the firstfruits of your harvest unto the priest: And he shall wave the sheaf before the LORD, to be accepted for you: on the morrow after the sabbath the priest shall wave it. And ye shall offer that day when ye wave the sheaf an he lamb without blemish of the first year for a burnt offering unto the LORD” (Lev 23:5, 10—12). That is why the year had to be extended by one month if the grains were not ripe, and the lambs too young. The extended 13-month year was usually called embolismic.
Around 500 NE, the Jewish calendar was reformed. The beginning of the year was moved to the month of Tisri, and Molad became the starting point for counting months (the astronomic new moon). Also, specific rules were introduced for alternating the number of days in a month and adding an extra month, which facilitated the process for calculating dates.
The reference point of the Jewish calendar was moved to the foundation of the world, Tisri 1 (“the new moon of creation”), which corresponded to October 6/7, 3761 BNE in the Julian calendar.
The principles of the Jewish calendar
In the Jewish calendar, the 13th month was inserted according to the 19-year cycle: specifically, for years 3, 6, 8, 11, 14, 17 and 19. The extra month was added before Adar and was called Adar 1 (Adar Rishon). Adar, then, became the next month and was named Adar 2 (Adar Sheni, Adar Bet, Beadar). All the religious feasts of the month of Adar were transferred to this month.
The number of days in a year varied from 353 to 385. There were six variants:
a) short, or insufficient year (hasarin) had 353 days (standard) or 383 days (embolismic);
b) the proper, or full year (kesedran) had 354 days (standard) or 384 days (embolismic);
c) the excessive year (shalamim) had 355 days (standard) or 385 days (embolismic).
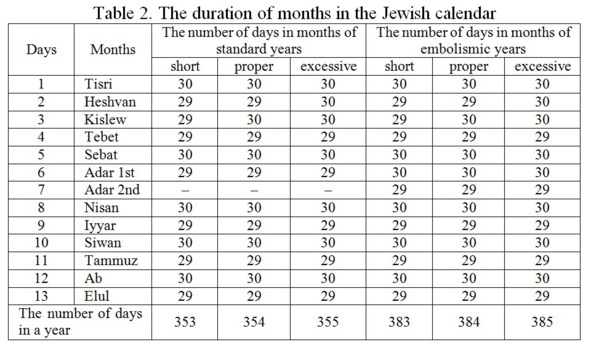
The rationale behind such a complex system is the desire of the Jews to observe all the Talmudic religious traditions. It is only possible to fulfill the several hundreds of Talmudic prescriptions if the 1st of Tisri (the beginning of the new year) falls on Monday, Tuesday, Thursday or Saturday, and the 15th of Nissan (the Jewish Passover) falls on Tuesday, Thursday, Saturday or Sunday.
So, in any given year, if you know which days of the week fall on the 1st of Tisri and the 15th of Nissan, you can understand whether the year is insufficient, proper or excessive, that is, you will know how many days it consists of.

One other percularity of the Jewish calendar is that 24-hour days are counted from sunset, not from midnight. This was believed to be the pattern of creation in the corresponding Genesis account: “And the evening and the morning were the first day” (Gen 1:5).
The formulas of Gauss
Around the year 1800, the German mathematician Carl Friedrich Gauss (1777 – 1855) introduced formulas for calculating the dates for Christian Easter and the Jewish Passover. These formulas made chonological calculations much easier.
The procedure for calculating the date of the Jewish Passover (Nissan 15) is as follows:
1) A=R+3660,
where “A” is the year according to the Jewish calendar; “R” is the year NE.
2) a= (12A+17) mod 19,
where “mod 19” is the remainder of the division by 19.
3) b=A mod 4.
4) M+m= (32,0440933+1,5542418a+0,25b-0,00317779A),
where “M” is the integer part, and “m” is the fractional part.
5) c= (M+3A+5b+5) mod 7.
So, three variants are possible:
1) is c=1, a> b and m≥0.63287037, then the Jewish Passover (Nissan 15) falls on M+2 March in the Julian calendar.
2) if c=2, 4 or 6, and also when c=0, a> 11 and m≥0,89772376, then the Jewish Passover falls on M+1 March.
3) in all other cases it falls on M in March.
If the resulting value is greater than the number of days in March, you should subtract 31. The result will correspond to a date in April.
For example, let us calculate the date for the Jewish Passover in 2016:
1) A=5776.
2) a=17.
3) b=0.
4) M+m=40,11128886.
M=40, m=0,11128886.
5) c=6.
Since c=6, you should add 1 to M=40 and subtract 31. So, in 2016, the Jewish Passover (Nissan 15) falls on April 10 in the Julian calendar, which corresponds to April 23 in the Gregorian calendar. As noted above, the 24-hour day in the Jewish calendar begins at sunset. That is why the 15th of Nissan in this case begins in the evening of April 9 and ends in the evening of April 10.
The procedure for calculating the date of Christian Easter using the Gauss formula is as follows:
1) a=R mod 19,
where “R” is the year NE; “mod 19” is the remainder after the division by 19.
2) b=R mod 4.
3) c=R mod 7.
4) d= (19a+15) mod 30.
5) e= (2b+4c+6d+6) mod 7.
Three variants are possible:
1) if the sum of (d+e) does not exceed 9, then Christian Easter falls on March (22+d+e).
2) is (d+e) ≥10, then Easter falls on April (d+e-9).
For example, let us calculate the date for Easter in 2016:
1) a=2.
2) b=0.
3) c=0.
4) d=23.
5) e=4.
Since (d+e) exceeds 9, let us calculate (d+e-9) =18. So, in 2016, Orthodox Christian Easter falls on April 18 of the Julian calendar, which corresponds to May 1 in the Gregorian calendar.
The Julian period and calendar
Historians and annalists often deal with calendar calculations which involve various types of dates. To simplify the process for converting dates from one calendar to another, the “system of Julian days” or “continuous day count” was introduced. In 1583, the French scholar Joseph Justus Scaliger (1540 – 1609) came up with the idea of the so-called “Julian period”. He named this method of calculation in honor of his father Julius Caesar Scaliger (1484 – 1558), the famous humanist and scholar.
Joseph Scaliger suggested a chronological scale against which any historical date could be aligned. The starting point for counting the “Julian days” (JDN=0) was set to January 1, 4713 BNE, which was the era “from the foundation of the world” according to Scaliger. Then, the JDN value would increase by one every day. So, January 2, 4713 BNE equals to JDN=1 and so on. For example, January 1 of the 1st year NE is JDN=1721424.
In 1849, John Herschel (1792 – 1871) suggested expressing all the dates though the JD value, which is the number of days that passed since the beginning of the Scaliger cycle. The difference between the Julian date (JD) and the Julian day number (JDN) is that the former contains a fractional part which indicates the time of 24-hour day. It was agreed that the beginning of the Julian day would be noontime according to Greenwich Mean Time. So, the midnight of January 1 of the 1st year NE corresponds to JD=1721423.5. Note that the JD=1721424 will accumulate only by the noon of the specified day, because the count was started at noon January 1, 4713 BNE (the “zero point”). To make our calculations easier, we will use the rounded value of the Julian date or the Julian day number (JDN).
The procedure for calculating the Julian day number (JDN) for a specific Julian calendar date is as follows:
1) a= [(14-month) /12].
2) y=year+4800-a.
3) m=month+12a-3.
4) Julian day number:
JDN=day+ [(153m+2) /5] +365y+ [y/4] -32083.
Where “year” is the year of NE; “month” is the number of the month; “day” is the day of the month; value in brackets is the integer part.
Knowing the JDN, you can find the day of the week by calculating the remainder of the division of JDN by 7. Based on the remainder value, the days of the week are distributed as follows: 0 – Monday, 1 – Tuesday, 2 – Wednesday, 3 – Thursday, 4 – Friday, 5 – Saturday, 6 – Sunday.
For example, let us calculate the Julian day number for the Jewish Passover in 2016 (April 10 in the Julian calendar):
1) a=0.
2) y=6816.
3) m=1.
4) JDN=2457502.
Remainder of division (JDN mod 7) =5, therefore, it is Saturday.
Finding dates based on the Julian days
The method of calculation based on the Julian days can be useful, for example, for finding the date for Tisri 1. We don’t know the interval between Nisan 15 and Tisri 1 within one year. But the interval between Tisri 1 of the year to be found and Nisan 15 of the previous year is always 163 days because Nisan, Iyyar, Siwan, Tammuz, Ab, and Elul have an unchanging number of days. If you know the Julian day number for Nisan 15, you can, by adding 163, find the Julian day number for Tisri 1 of the following year.






