Физика. Порядок вещей, или Осознание знаний. Книга 2

Ускорение Кориолиса в первом варианте по Матвееву это изменение скорости тела, движущегося радиально внутри вращающейся системы в направлении, перпендикулярном радиусу вращения. Это общепринятое в классической физике определение ускорения Кориолиса.

На стр. 404 Матвеев пишет:

«Скорость вдоль радиуса Vr изменяется за это время (Δt) по направлению, а скорость Vn, перпендикулярная радиусу, изменяется как по направлению, так и по абсолютному значению. Полное изменение составляющей скорости, перпендикулярной радиусу, равно:

ΔVn = Vn1 – Vn2 * cos α + Vr * Δα ≈

≈ ω * r1 – ω * r2 + Vr * ω Δt = V * Δr + Vr * ω Δt (66.3)

где учтено, что cos α ≈ 1

Следовательно, кориолисово ускорение в пределе при Δt→0 равно:

wк = ω * Δr / dt + Vr * ω = 2 * Vr * ω (66.4)».

Вообще говоря, поворот вектора переносной скорости происходит под действием переносного центростремительного ускорения, которое проявляется в радиальном направлении и потому не имеет никакого отношения к поворотному ускорению Кориолиса. Поэтому векторы (Vn1) и (Vn2) можно сравнивать по абсолютной величине непосредственно без проецирования (Vn2) на тангенциальное направление с учётом (cos α). Всё намного серьёзнее, чем ненужное в данном случае проецирование и связано с неправильными физическими представлениями классической физики о явлении Кориолиса.

Из выражения (66.4) следует, что ускорение Кориолиса – это изменение абсолютной скорости в направлении перпендикулярном радиусу, которое обеспечивается двумя самостоятельными независимыми ускорениями:

1. Ускорением, характеризующим приращение линейной скорости переносного вращения по абсолютной величине;

2. Ускорением, характеризующим приращение радиальной скорости относительного движения по направлению.

Этим собственно и объясняется «двойка» в ускорении Кориолиса. Но если предположить, что эти две якобы самостоятельные интерпретации ускорения Кориолиса представляют собой одну и ту же физическую величину, достаточную, как для поворота радиально скорости, так и для приращения тангенциальной скорости по величине, то под сомнение подпадает именно её удвоение.

4.1.1. Физический смысл явления Кориолиса определяется Истинной силой Кориолиса-Кеплера из второго закона Кеплера

В соответствии со вторым законом Кеплера, ошибочно называемом в классической лже динамикой вращательного движения законом сохранения не существующей в природе физической величины – момента импульса, линейная и угловая скорость при изменении радиуса изменяется обратно пропорционально первой и второй степени радиуса соответственно. Но как известно единственной причиной изменения скорости (импульса) неизменной массы является только сила. Найдём эту силу Кеплера (см. рисунок ниже).

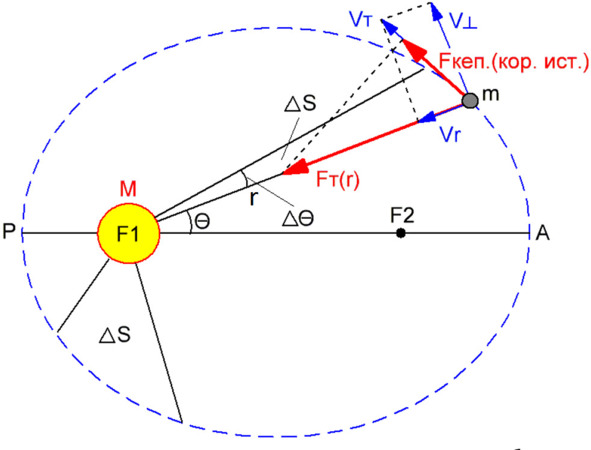
Из рисунка видно, что единственная сила, которая может быть причастна к изменению тангенциальной скорости тела (m) – это проекция силы тяготения на касательную к траектории движения тела, она же радиальная сила (Fт (к)). Это и есть сила Кеплера, она же истинная сила Кориолиса (Fкеп. (кор. ист.). Из формулировки второго закона Кеплера (1609 г.) следует, что радиус-вектор обращающегося тела заметает равные площади за равные промежутки времени (см. рисунок выше). При этом площадь, описываемая радиус-вектором за малое время Δt, приближенно равна площади треугольника с основанием r * Δθ и высотой r:

dS = ½ * r2 * Δθ

dS / dt = ½ r2 * dθ / dt = ½ * r * V┴ = ½ * ω * r2 = const.

А поскольку секторальная скорость (dS / dt) постоянна, то её производная по времени S’t равна нулю:

S« (t) = ½ (r’ (t) * V┴ + r * V┴» (t)) = 0

где

r’ (t) = Vr – радиальная скорость

V┴» (t) = aК ист – ускорение Кориолиса Истинное;

V┴ = ω * r

Тогда:

Vr * ω * r + r * aК ист. = 0

Сократив на r, получим:

aК ист = – Vr * ω

Тогда Истинная сила Кориолиса равна:

Fк ист = аК ист * m = – Vr * ω * m

Не трудно показать связь второго закона Кеплера с так называемым законом сохранения момента импульса или углового момента классической лже динамики вращательного движения.

L = m * ω * r2

Тогда:

dS / dt = ½ * L / m

Таким образом, угловая скорость при радиальном движении определяется не только чисто геометрическим масштабированием при неизменной линейной скорости с масштабным коэффициентом-радиусом, что совершенно очевидно и без каких-либо выводов, но и за счёт истинной силы Кориолиса-Кеплера, которая физически изменяет линейную скорость на каждом текущем радиусе. При этом истинная сила Кориолиса-Кеплера, тормозящая тело при радиальном движении от центра вращения и разгоняющая его при движении к центру, вдвое меньше классической силы Кориолиса.

По определению сила Кориолиса проявляется только, как противодействие поддерживающей вращение силе, возникающей за счёт инерции вращения базовой системы с неизменным радиусом. Однако поскольку одиночное тело (m) не имеет связи с базовой для него вращающейся системой, которая поддерживала бы его вращение за счёт инерции своей не изменяющей радиус массы, то в рассмотренном случае силы Кориолиса нет.

Как мы уже отмечали в главе (3.4.3) на примере радиального движения от центра вращения в результате ослабления связей с без массовым центром вращения часть энергии связи безвозвратно рассевается в окружающем пространстве. При этом энергия связи, необходимая для установления нового вращения тела на новом радиусе, может быть изъята только из кинетической энергии освобождающегося тела.

Отбор необходимой энергии осуществляется за счёт истинной силы Кориолиса-Кеплера, которая, как отмечалось выше, является тангенциальной проекцией радиальной силы на касательную к спирали. При этом угловая скорость тела уменьшается, как геометрически в результате масштабирования угловой скорости с масштабным коэффициентом-радиусом, так и за счёт непосредственного физического уменьшения линейной скорости силой Кеплера.

При движении к центру вращения этот механизм принципиально сохраняется с той лишь разницей, что необходимая энергия берётся из источника радиального движения. В классическом поворотном движении этим источником может быть либо источник сторонней поддерживающей силы, либо инерция условно массивного центра вращения (базовая вращающаяся система с неизменным радиусом).

Часть поддерживающей вращение силы компенсирует часть истинной силы Кориолиса-Кеплера. Эта равновесная часть поддерживающей силы и истинной силы Кориолиса не причастна к ускорению Кориолиса и к силе реакции на вызывающую его силу, т.к. соответствующие части обоих сил здесь взаимно компенсируются. Дальнейшее восстановление угловой скорости до исходного значения и выше осуществляется только за счёт оставшейся части поддерживающей силы с ускорением Кориолиса.

Как показано выше, истинная сила Кориолиса-Кеплера равна ровно половине классической силы Кориолиса. Следовательно, при неизменной угловой скорости на компенсацию истинной силы Кориолиса-Кеплера уходит ровно половина поддерживающей силы. При этом сила Кориолиса, как реакция на реальное ускорение Кориолиса, т.е. на ответственную за него часть поддерживающей силы, вдвое меньше классической силы Кориолиса, которая на половину определяется статическим равновесием.

Таким образом, классическая сила Кориолиса это либо, полу фиктивная обычная сила, либо полу обычная фиктивная сила.

Если путём компенсации истинной силы Кориолиса-Кеплера поддерживать на неизменном уровне только линейную скорость переносного вращения, то ускорение Кориолиса будет равно нулю. Возникающее при этом движение по спирали осуществляется только с центростремительным ускорением, которое также равно нулю, если речь идёт о вращении на уровне не менее цикла его формирования. На первый взгляд это выглядит парадоксальным. Однако гораздо более парадоксально наличие реального ЦСУ в классической физике.

Равномерное движение по окружности так же, как и равномерное движение по прямой, осуществляется фактически в одном неизменном круговом «направлении», т.к. окружность при этом не изменяет своей постоянной конфигурации. Отклонений от неё, как и в случае движения по прямой – нет, а само движение в целом осуществляется при полном равновесии ЦБ и ЦС сил и постоянной линейной скоростью, т.е. равномерно. При этом постоянный поворот относительно центра вращения объясняется не внешней неуравновешенной силой, а одной из внутренних сил вращательного движения, действующей последней.

Это относится, в том числе и к движению по кругу отдельной материальной точки (тела). Действительно. Возврат на дальний радиус происходит по инерции, т.е. за счёт внутренних сил. Тут вопросов ни у кого не возникает. А для перехода на ближний радиус источник внешней силы сам должен двигаться по кругу неотступно от тела. Для этого ему нужен свой неотступный источник и так далее до бесконечности. Единственный способ избежать этой недостижимой в принципе бесконечности – это диаметрально уравновешенное движение, которое является внутренним движением вращающейся системы без ускорения.

В отсутствие замкнутого диаметрально уравновешенного кругового движения тела, которое осуществляется без ускорения, все внешние воздействия на него не являются центростремительными, а его ускорение не будет соответственно центростремительным. Без цикла формирования вращательного движения (ВД) это будут обычные разрозненные линейные силы и ускорения без какого-либо центра вращения и самого вращения. Это всего лишь абстрактная идеализация или аппроксимация под ВД.

Поскольку активная сила упругости по фазе изменения направления всегда опережает ньютоновскую силу инерции поэлементной поддержки, то, несмотря на отсутствие реального геометрического ускорения во вращательном движении в целом, результирующая сила неизменно отклоняется в сторону центра вращения, формируя общую макро кинематику вращательного движения. Иными словами в случае равновесия двух противодействующих сил, разнесённых по фазе (по времени), движение всегда осуществляется в сторону силы, действующей последней. В этом легко убедиться в простом мысленном эксперименте.

Пусть на тело действуют две равные по величине, но противоположные по направлению силы. При этом в соответствии с первым законом Ньютона тело находится в покое или движется равномерно и прямолинейно. Теперь уберём одну из сил. Тело начнёт движение под действием оставшейся неуравновешенной силы. Но, как только противодействие восстановится, тело вновь остановится или вернётся к предыдущему равномерному и прямолинейному движению. Из этого следует, что состояние движения определяется последней действующей по времени неуравновешенной силой.

Поскольку во вращательном движении последней по времени всегда действует центростремительная сила упругости, то при равенстве центробежных сил инерции и центростремительных сил упругости, разнесённых по фазе, траектория равномерно отклоняется в сторону центра вращения. Этот процесс характеризуется в физике условно-академическим центростремительным ускорением без итогового ускорения. Если оборвать связующее тело, то последней по времени будет сила инерции. При этом вращательное движение вновь преобразуется в прямолинейное движение (см. гл. 3.2.1).

Ну, а если кто то хочет возразить, что ЦБ сила, которая уравновешивает ЦС силу приложена не к самому телу, а к связующему телу, то пусть ответит сам себе на вопрос за счёт чего же тогда поддерживается линейная скорость в направлении от центра вращения, если не за счёт ньютоновской инерции поэлементной поддержки, которая основана именно на реальных силах? И пусть поищет заодно, где у вращающейся массы заканчивается связующее тело и начинается непосредственно само вращающееся тело (см. главу 3.2.).

В классической физике истинная сила Кориолиса-Кеплера отсутствует. Поэтому в расчёте ускорения Кориолиса она ошибочно исходит из приращения движения, соответствующего полной поддерживающей силе, что приводит к удвоению ускорения Кориолиса. Это требует качественной и соответственно количественной коррекции классической версии явления Кориолиса и анализа причин, по которым классическое дифференцирование не видит этой ошибки.

Начнём с прямолинейного движения. На рисунке (4.1.1.1) показаны два отдельных участка прямолинейного равноускоренного движения с координатами (18 м, 21 м) и (21м, 26 м) с секундным интервалом между каждой указанной в скобках парой координат.

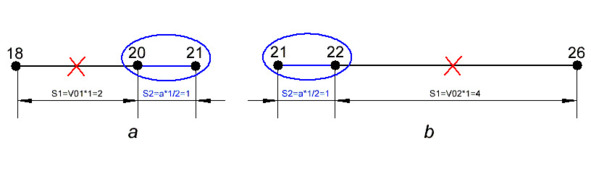
Рис. 4.1.1.1

В физике есть известная всем школьная формула пути для равноускоренного движения (S = V0* t + a * t2 / 2), из которой следует, что ускорение равно (a = 2 * (S – V0 * t) / t2). Как видно, пресловутая двойка не является эксклюзивной исключительно только для явления Кориолиса. Она имеет принципиальное значение для определения ускорения через приращение пути любого равноускоренного движения, т.к. средняя скорость, которая и определяет пройденное расстояние, вдвое меньше мгновенной скорости, достигнутой за счёт ускорения за то же самое время. Однако при определении ускорения через дифференцирование координат эту формулу не используют, т.к. для неё недостаточно одних только координат, нужна ещё и начальная скорость.

Если координаты движения можно легко измерить в любой заданной системе отсчёта, то вычленить начальную скорость в составе переменного движения в двух координатах (18 м, 21 м) или (21м, 26 м), как на рисунке 4.1.1.1 a и b, без дополнительных данных не представляется возможным. Поэтому приращение скорости и ускорения переменного движения определяется в классической физике через дифференцирование разности между парами координат по трёхточечной схеме. В нашем примере это по-прежнему координаты (18 м, 21 м) и (21м, 26 м) с секундным интервалом между каждой парой (см. Рис. 4.1.1.2). Но с учётом общей точки (21 м) мы получаем общую трёхточечную схему для двух смежных участков (18м, 21м, 26м).

Рис. 4.1.1.2

Как показано на рисунке, при вычитании отрезков (26 – 21) минус (21 – 18) расстояние (S1 и S4), пройденное с начальной скоростью (V01), а также расстояние (S2) и (S5), пройденное за счёт ускорения, взаимно уничтожаются. Остаётся только отрезок пути (S3 = ∆V * t), где (∆V) – разность средних скоростей на участках (18 м, 21 м) и (21м, 26 м). Тогда ускорение определяется второй производной приращения по времени (a = d2S3 / dt2) между парами координат (26 – 21) и (21 – 18), равному (S3). Это соответствует школьной формуле пути при равноускоренном движении только без двойки в знаменателе, т.к. сравниваются уже готовые именно средние скорости.

Пресловутая двойка фигурирует и в выводе ЦС ускорения по трёхточечной схеме. Однако это так же, как и в случае с прямолинейным ускоренным движением связано не с удвоением ускорения, а со средней скоростью ускоренного движения. Покажем это на рисунке (4.1.1.3).

Приращение пути за счёт ЦСУ равно:

∆rx = (DL – D”2») – (D”2» – DK) = DL – 2 * D”2» + DK

а = (cos (ωt) * (DL + DK) – 2 * D”2») / t2

Поскольку DL = DK, а угловая скорость (ω) – постоянная, то

|DL – D”2»| = |D”2» – DK|

DL + DК = 2 * D”2»

Тогда:

а = (cos (ωt) – 1) * 2 * D”2») / t2

Как видно, здесь двойка относится вовсе не к удвоению приращения пути за счёт ускорения. Это промежуточный результат связанный с вычислением средней скорости, что становится очевидным при разложении функции (cos (ωt) – 1) в ряд Тейлора:

cos (n) – 1 = – 1 = -n2 / 2…

Тогда:

a = – (((ωt) 2 / 2) * 2 * D”2») / t2 = ω2 r

После сокращения (2) и (t2), получаем

a = – = ω2 r,

где D”2» = r

На рисунке (4.1.1.3) приведена классическая трёхточечная схема применительно к криволинейному движению. Временной интервал между точками (1, 2, 3), если считать по порядку по ходу движения, как и прежде – одна секунда. Очевидно, что если бы не было радиальной скорости, то все три радиуса-вектора (DK), (D «2»), и (DL) были бы одинаковыми. При этом разница проекций (DK) и (DL) на ось (Y) была бы равна нулю (ВD – DF = 0), что означает отсутствие ускорения вдоль тангенциального направления (Y).

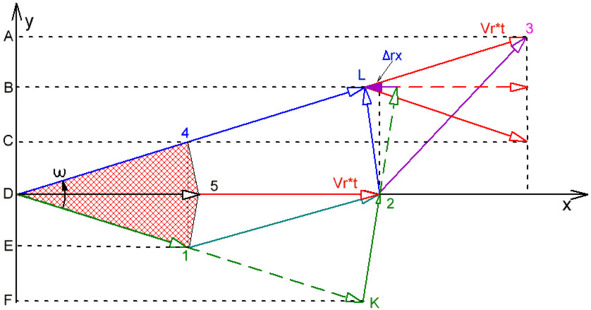
Рис. 4.1.1.3

Очевидно, что с учётом радиального движения радиус-вектор (D «1») будет короче радиуса-вектора (DK) на («1» К = Vr * t * sin (ω * t)), а радиус-вектор (D «3») длиннее радиуса-вектора (DL) на величину (L «3» = Vr * t * sin (ω * t)). А поскольку разность проекций на ось (Y) областей (D «4» «5») и (D «5» «1») равна нулю (красная штриховка), то приращение вдоль оси (Y) соответствует двум проекциям приращения радиуса – (AC = АВ + ВС = 2 * Vr * t * sin (ω * t)), или для малых углов (AC = 2 * Vr * ω * t2). Это и есть классическое математическое подтверждение двойки в ускорении Кориолиса. Однако это справедливо только в отсутствие истинной силы Кориолиса-Кеплера.

Естественно, что прирост средней скорости даёт и среднее ускорение при вычислении. При этом стопроцентная точность трёхточечной схемы обеспечивается только при равноускоренном движении на всём протяжении обоих смежных участков. В противном случае одинаковое среднее ускорение может быть получено при разных ускорениях на каждом участке с максимальным отличием в два раза, когда приращение координат на одном из участков достигнуто без ускорения, т.е. с нулевым ускорением за счёт неизменной скорости. Поворотное движение это на наш взгляд, как раз то случай.

В поворотном движении нет идеального ВД ни вектора тангенциальной скорости, ни вектора радиальной скорости. Радиальное движение делает незавершёнными, как цикл ВД тангенциальной скорости, так и цикл ВД радиальной скорости. При этом, очевидно, поворот вектора радиальной скорости за счёт половины поддерживающей силы осуществляется через механизм отражения, с ускорением которого и осуществляется и приращение тангенциальной скорости по величине. Более подробно о механизме формирования поворотного движения будет изложено в следующей главе (4.1.2.).

Как показано выше, если путём компенсации истинной силы Кориолиса-Кеплера поддерживать на неизменном уровне только линейную скорость переносного вращения, то ускорение Кориолиса будет равно нулю. Именно это и происходит в поворотном движении. Однако классическая трёхточечная схема не видит этого обнуления половины ускорения Кориолиса, т.к. в графическом решении не отражается компенсация половины поддерживающей силы за счёт силы Кеплера. В ней есть только общее приращение движения без учёта истинного вклада в него поддерживающей силы.

Трёхточечная схема отсекает только начальную скорость от измеряемого участка, исключая тем самым обеспечиваемое начальной скоростью приращение пути без ускорения. Но то, что происходит внутри измеряемого участка не видит ни одна графическая схема. Это можно учесть исключительно только аналитически и условно отобразить графически. А анализ показывает, половина поддерживающей силы тратится на компенсацию силы Кеплера. Это означает, что половину приращения, определяемого по трёхточечной схеме тело проходит без ускорения с постоянной скоростью.

Таким образом, полное напряжение Кориолиса в статике действительно соответствует классической силе Кориолиса (Fпк = 2 * m * Vr * ω). Однако динамические ускорение и сила Кориолиса оказываются при этом вдвое меньше классических аналогов (акд = Vr * sin (ω * t) / t = Vr * ω, Fкд = m * Vr * ω).

4.1.2. Механизм формирования поворотного ускорения Кориолиса

Радиальное движение может изменить своё направление только при взаимодействии тела с вращающимся радиусом в момент, когда он изменяет своё угловое положение по отношению к прямолинейному радиальному движению. При этом взаимодействие тела с радиусом будет происходить по типу отражения (см. Рис 4.1.2.1, положение 2), ускорение которого никто не подразделяет на самостоятельные составляющие в виде ЦСУ по изменению направления радиальной скорости и ускорения, обеспечивающего приращение линейной скорости переносного вращения.

Оторвавшись после отражения от физического радиуса-направляющей, тело движется по инерции, не меняя больше углового положения и абсолютной величины вектора скорости. При этом тело удаляется от бывшего радиуса вдоль касательной к переносной окружности со скоростью, равной проекции своей абсолютной (отражённой) скорости на касательную к окружности текущего переносного вращения. Это и есть приращение тангенциальной скорости.

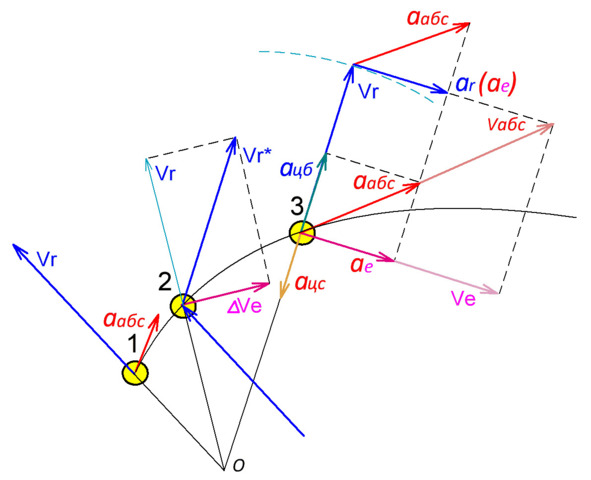
Рис. 4.1.2.1

Одновременно тело удаляется и от центра вращения с радиальной проекцией абсолютной скорости (Vr). При этом угловое положение вращающегося физического радиуса продолжает непрерывно изменяться и после завершения взаимодействия отражения. В результате, физический радиус, который в данном случае совпадает с математическим радиус-вектором постепенно догоняет вектор скорости тела по угловому положению (см. Рис 4.1.2.1, поз. 1,2).

Очевидно, что все точки вращающегося радиуса имеют свою переносную скорость, которая тем больше, чем дальше она находится от центра вращения. Поэтому, как бы ни была велика отражённая инерционная скорость тела в переносном направлении, одновременно удаляющегося от центра вращения и в радиальном направлении, его рано или поздно настигнет соответственная точка на радиусе, который следует за телом с неизменной угловой скоростью за счёт поддерживающей силы.

Другими словами в процессе радиального движения тело неизбежно переместится в область переносного вращения, в которой тангенциальная скорость точки на радиусе сопоставима со скоростью самого тела в этом направлении, что приведёт к началу нового цикла, но уже на базе новой начальной линейной скорости При этом новое отражение приведёт к новому повороту и новому приращению линейной скорости.

Если при встрече тела с новой точкой радиуса совпадения исходных параметров в виде углового положения и величины вектора скорости не произойдёт, то заработает механизм отрицательной обратной связи, регулирующий эти параметры. При этом каждое последующее отражение будет происходить при меньшем различии исходных параметров взаимодействия, которые вдруг по какой-либо причине не совпали с «первой попытки». Так будет происходить, вплоть до их полного совпадения.

В результате, в конце цикла относительная скорость точки на радиусе и тела в переносном направлении становится равной нулю, а скорость относительного движения поворотного движения направлена строго вдоль радиуса. На этом полный цикл формирования поворотного движения и ускорения Кориолиса заканчивается (см. Рис. 4.1.2.1, поз. 3), после чего начинается новый абсолютно идентичный предыдущему цикл поворотного движения. Разумеется, всё это происходит на микроуровне.

В соответствии с механизмом отражения, ускоренное удаление тела от радиуса в новом после отражения направлении, определяется, как проекция его ускорения на перпендикуляр к отражающему радиусу, что и есть ускорение переносной скорости по абсолютной величине. Следовательно, ускорение радиальной скорости по направлению и ускорение переносной скорости по величине это одна и та же физическая величина, равная ускорению отражения.

Кто то может возразить, что с ЦСУ осуществляется изменение относительной радиальной скорости исключительно только по направлению. Следовательно, для изменения линейной скорости переносного вращения по абсолютной величине необходимо дополнительное самостоятельное ускорение, как это декларируется в классической физике и в частности у Матвеева (см. фотокопию вначале настоящей главы). Однако, как показано в главе (3.1. И 3.2.) изменение скорости по направлению принципиально не возможно без изменения её абсолютной величины, которая изменяется уже в новом направлении.

Естественно, что абсолютная величина каждого мгновенного ускорения отражения внутри цикла формирования ускорения Кориолиса может превышать среднее ускорение цикла не только вдвое, но и в десятки раз, что не меняет физического смысла ускорения Кориолиса. В конечном итоге тело не может двигаться в направлении линейной скорости переносного вращения быстрее соответственной точки на радиусе, как мяч не может двигаться быстрее футболиста.

Если тело получит, например, в 10 раз большее мгновенное ускорение отражения, чем среднее обобщённое ускорение Кориолиса, то к моменту отрыва от радиуса оно наберёт и в 10 раз большую скорость. Но при этом и радиусу, вращающемуся с постоянной угловой скоростью, понадобится в 10 раз большее время, чтобы догнать тело. При этом среднее ускорение Кориолиса при неизменной угловой скорости и неизменной величине скорости относительного движения количественно останется неизменным: