
Полная версия
Опасная идея Дарвина: Эволюция и смысл жизни
«Отчетливо выраженные» виды, несомненно, существуют – задача книги Дарвина состоит в объяснении их происхождения, – но сам автор препятствует попыткам отыскать «принципиальное» определение понятия вида. Разновидности – продолжает он настаивать – всего лишь «зарождающиеся виды», и обычно две разновидности становятся видами не из‐за присутствия чего-либо (например, новой сущности для каждой группы), а из‐за отсутствия: некогда существовавшие промежуточные вариации (которые можно было бы назвать переходными этапами) в конце концов вымирают, оставляя две группы фактически репродуктивно изолированными, а также отличающимися друг от друга по своим характеристикам.
В «Происхождении видов» излагается чрезвычайно убедительное доказательство первого дарвиновского тезиса – исторического факта эволюции как причины происхождения видов, и соблазнительно наглядное свидетельство в пользу второго тезиса – что фундаментальным механизмом, ответственным за «наследование с изменением», является естественный отбор52. Здравомыслящие читатели просто не могли более сомневаться, что виды эволюционировали в течение невероятно продолжительного времени, как утверждал Дарвин, но преодолеть добросовестный скептицизм относительно предложенного им механизма естественного отбора было сложнее. Прошедшие годы увеличили доверие к обоим тезисам, но не изгладили разницу между ними53. Свидетельств в пользу эволюции предостаточно: не только из области геологии, палеонтологии, биогеографии и анатомии (бывших основными источниками материала для Дарвина), но и из молекулярной биологии и любой другой отрасли наук о жизни. Говоря начистоту, сегодня любой человек, сомневающийся в том, что разнообразие жизни на планете порождено процессом эволюции, – просто невежда; в мире, где трое из четырех научились читать и писать, у такого невежества нет оправданий. Однако сомнения в способности дарвиновской идеи естественного отбора объяснить этот эволюционный процесс остаются интеллектуально оправданными, хотя, как мы увидим, подобный скептицизм становится все сложнее обосновать.
Итак, хотя в своих исследованиях эволюции Дарвин вдохновлялся и руководствовался идеей естественного отбора, окончательный результат изменил порядок обоснования: Дарвин так убедительно доказал, что виды должны были эволюционировать, что затем смог использовать этот результат для обоснования более радикальной идеи – идеи естественного отбора. Он описал механизм или процесс, который, согласно его доводам, мог иметь все эти последствия. Скептикам был брошен вызов: смогут ли они доказать ошибочность дарвиновских аргументов? Смогут ли они показать, что естественный отбор не мог иметь описанных последствий?54 Или смогут ли они хотя бы описать другой процесс, у которого были бы те же результаты? Что еще может привести к эволюции, если не описанный Дарвином механизм?
Этот вызов, по сути, выворачивает наизнанку затруднение Юма. Юм сдался, поскольку не мог вообразить, как что-либо кроме Разумного Демиурга смогло бы стать причиной приспособлений, доступных наблюдению каждого. Или, точнее, Филон Юма вообразил несколько разных альтернатив, но Юм просто не мог воспринять их всерьез. Дарвин описывал, как Неразумный Демиург мог за огромный период времени создать все эти приспособления, и доказал, что некоторые промежуточные стадии, которые для этого потребовались бы, и в самом деле имели место. Брошенный воображению вызов изменился: при всех указанных Дарвином красноречивых признаках исторического процесса – так сказать, всех мазках кисти художника, – может ли кто-нибудь теперь вообразить, как все эти последствия породил какой-либо другой процесс кроме процесса естественного отбора? Бремя доказательства так решительно было им переложено, что ученые зачастую обнаруживают, что столкнулись с чем-то вроде зеркального отражения затруднения Юма. Столкнувшись с, на первый взгляд, убедительным возражением против естественного отбора, которое невозможно проигнорировать (ниже мы поговорим о наиболее ярких примерах подобных возражений), они склонны рассуждать следующим образом: Я (пока что) не понимаю, как опровергнуть это возражение или преодолеть это затруднение, но, поскольку я не могу вообразить, что еще кроме естественного отбора может привести к подобным результатам, мне придется допустить, что возражение это мнимое; так или иначе естественного отбора должно быть вполне достаточно для объяснения.
Прежде чем кто-нибудь набросится на меня и возопит, что я только что признал дарвинизм столь же бездоказательной верой, как и естественная религия, следует вспомнить, что существует фундаментальное различие: принеся клятву верности естественному отбору, эти ученые затем принимали на себя обязанность показать, как можно преодолеть сложности, вытекающие из их мировоззрения, и снова и снова преуспевали в этом. В процессе фундаментальная дарвиновская идея естественного отбора по-разному формулировалась, расширялась, прояснялась, взвешивалась и углублялась – каждое разрешенное затруднение делало ее сильнее. С каждым новым триумфом ученые все больше убеждались, что они на верном пути. Разумно полагать, что в результате таких непрестанных атак ложная идея к настоящему моменту уже неизбежно была бы повержена. Конечно, это не окончательное доказательство, а всего лишь весьма убедительное соображение. Одна из целей этой книги – объяснить, почему идея естественного отбора представляется явным победителем несмотря даже на то, что в некоторых случаях существуют неразрешенные проблемы с ее применением.
4. Естественный отбор как алгоритмический процесс
Какой предел может быть положен этой силе, действующей в течение долгих веков и строго исследующей всю конституцию и образ жизни каждого существа, благоприятствуя полезному и отвергая вредное? Я не усматриваю предела деятельности этой силы, медленно и прекрасно адаптирующей каждую форму к самым сложным жизненным отношениям.
Чарлз Дарвин 55Второе, на что следует обратить внимание в формулировке Дарвина, – то, что он излагает свой закон в виде формального дедуктивного вывода: если условия выполняются, определенный результат неизбежен56. Приведем ее снова, выделив некоторые ключевые термины жирным шрифтом.
Если при меняющихся условиях жизни органические существа представляют индивидуальные различия почти в любой части своей организации, а это оспаривать невозможно; если в силу геометрической прогрессии возрастания численности ведется жестокая борьба за жизнь в любом возрасте, в любой год или время года, а это, конечно, неоспоримо; если вспомнить бесконечную сложность отношений органических существ (как между собой, так и к их жизненным условиям), в силу которых бесконечное многообразие строения, конституции и привычек полезно для этих существ; если принять все это во внимание, то крайне невероятно, чтобы никогда не встречались вариации, полезные каждому существу для его собственного благополучия, точно так же, как встречались многочисленные вариации, полезные для человека. Но если полезные для какого-нибудь органического существа вариации когда-либо встречаются, то особи, характеризующиеся ими, конечно, будут обладать наибольшей вероятностью сохранения в борьбе за жизнь, а в силу строгого принципа наследственности они обнаружат наклонность производить сходное с ними потомство. Этот принцип сохранения, или выживания наиболее приспособленного, я назвал Естественным отбором57.
Основной дедуктивный аргумент краток и прост, но сам Дарвин писал о «Происхождении видов» как о «едином длинном доказательстве». Так и есть, ведь книга состоит из доказательств двух видов: логического доказательства того, что процесс определенного рода с необходимостью будет приводить к определенного рода результату, и эмпирического доказательства того, что необходимые для протекания такого рода процесса условия в действительности существовали в природе. Дарвин подкрепляет логическое доказательство мысленными экспериментами – «воображаемыми примерами»58, – которые показывают, как выполнение таких условий могло в действительности привести к результатам, на объяснение которых он притязает, но, чтобы изложить довод полностью, ему нужна целая книга, поскольку он приводит множество с трудом добытых эмпирических фактов, чтобы убедить читателя, что эти условия выполнялись снова и снова.
Стивен Джей Гулд59 позволяет нам оценить важность этой особенности дарвиновского аргумента, рассказывая анекдот о Патрике Мэтью, шотландском натуралисте, который – к слову о любопытных исторических фактах – на много лет опередил Дарвина, описав механизм естественного отбора в приложении к опубликованной им в 1831 году книге «Плавник и лесокультура». На заре дарвиновского восхождения к славе Мэтью опубликовал (в Gardeners’ Chronicle!60) письмо, в котором заявил о своем приоритете: Дарвин великодушно его признал и оправдал свою неосведомленность, отметив, что Мэтью избрал для обнародования открытия издание, не привлекшее широкого интереса читателей. В ответ на извинения Дарвина Мэтью написал:
Я сформулировал концепцию этого закона Природы интуитивно, описывая самоочевидный факт, практически без усилий и сосредоточенного обдумывания. Кажется, у г-на Дарвина больше прав на это открытие, чем у меня – мне оно открытием не показалось. Он вывел его, опираясь на индуктивные умозаключения, неторопливо и с должной осторожностию продвигаясь от факта к факту, тогда как я, лишь бросив беглый взгляд на устройство Природы, счел это появление видов в результате отбора a priori очевидным фактом – аксиомой, на которую надо лишь указать, чтобы ее признали непредубежденные и достаточно быстро схватывающие умы61.
Однако непредубежденные умы вполне могут испытывать сомнения относительно новой идеи – по причине благоразумного консерватизма. Дедуктивные аргументы печально известны своей ненадежностью. То, что кажется «само собой разумеющимся», рассыплется из‐за незамеченной детали. Дарвин понимал, что лишь беспощадно подробное перечисление доказательств существования постулированного им исторического процесса будет – или должно быть – достаточно убедительным, чтобы ученые отринули свои традиционные убеждения и восприняли его революционный взгляд, даже если его действительно можно было «вывести из аксиом».
***С самого начала были те, кому дарвиновское новаторское сочетание дотошного натурализма с абстрактными рассуждениями о природных процессах казалось сомнительным и нежизнеспособным гибридом. Оно представлялось невероятно правдоподобным, но так же обстоит дело со множеством схем мгновенного обогащения, которые на поверку оказываются трюками и надувательством. Сравните его со следующим законом работы фондовой биржи: покупай по низкой цене, продавай по высокой. Если следовать этому правилу, обязательно разбогатеешь. Не может не разбогатеть тот, кто последует этому совету. Почему он не работает? Он работает – для всякого, кому достаточно повезло действовать в соответствии с ним, но, увы, нет способа определить, что условия выполнены, до того, как действовать, руководствуясь ими, не станет слишком поздно. Дарвин предлагал скептически настроенному миру то, что можно бы было назвать схемой медленного обогащения, схемой, позволяющей создать Порядок из Хаоса без помощи Разума.
Своей теоретической силой дарвиновская абстрактная схема была обязана нескольким особенностям, на которые Дарвин достаточно решительно указывал и которые ценил выше, чем многие его сторонники; однако он не располагал терминологией, позволившей бы их недвусмысленно описать. Сегодня мы можем охарактеризовать их одним-единственным термином. Дарвин открыл мощь алгоритма. Алгоритм – это определенного рода формальный процесс, который (логически) неизбежно приводит к достижению определенного рода результата, когда бы тот ни «запускался» или ни реализовывался. Во времена Дарвина в алгоритмах не было ничего нового. Многие хорошо известные арифметические процедуры – например, деление в столбик или подведение баланса в чековой книжке – являются алгоритмами, и таковы же процедуры принятия решений при разыгрывании образцовой партии в крестики-нолики или расположении нескольких слов в алфавитном порядке. Сравнительно новым (и позволяющим нам бросить ценный ретроспективный взгляд на открытие Дарвина) было теоретическое размышление математиков и логиков о природе и мощи алгоритмов в целом; в XX веке это привело к появлению компьютера, что в свою очередь, разумеется, стало причиной гораздо более глубокого и наглядного понимания возможностей алгоритмов в целом.
Термин алгоритм восходит – через латинское слово algorismus – к раннеанглийскому algorisme (с ошибочным написанием algorithm), образованному от имени персидского математика, Мусы аль-Хорезми, чья написанная примерно в 835 году н. э. книга о математических действиях в XII веке была переведена на латынь Аделардом Батским или Робертом Честерским. Идея, что алгоритм является надежной и в некотором роде «механической» процедурой, существовала на протяжении столетий, но лишь в 1930‐х годах в новаторской работе Алана Тьюринга, Курта Гёделя и Алонзо Черча было в первом приближении зафиксировано современное понимание этого термина. Нам будут важны три основные особенности алгоритмов, и каждую не так-то просто определить. Более того, каждая усугубила замешательство (и тревогу), все еще мешающие нам размышлять о революционном открытии Дарвина, так что на страницах этой книги нам неоднократно придется возвращаться к этим вводным замечаниям и переосмыслять их.
1. Безразличие к материалу: деление в столбик можно с равным успехом осуществлять, используя карандаш или ручку, бумагу или пергамент, неоновые огни или дымовой след самолета – и прибегая к какой угодно системе символов. Осуществимость процедуры основана на ее логической структуре, а не на конкретных особенностях использованных в данном случае материалов и лишь пока эти конкретные особенности позволяют в точности выполнять предписанные действия.
2. Базовая неразумность: хотя сам проект процедуры может быть блестящим или приводить к великолепным результатам, каждый конкретный ее шаг, а также переходы между ними чрезвычайно просты. Насколько они просты? Достаточно просты, чтобы их мог осуществить прилежный дурак – или попросту механическое устройство. Согласно известной «школьной» аналогии, алгоритмы – это своего рода рецепты, составленные так, чтобы им могли следовать поварята. В кулинарной книге, предназначенной для шеф-поваров, мы можем прочитать: «Варите рыбу в подходящем вине на медленном огне до полуготовности», – но описывающий тот же процесс алгоритм начнется так: «Выберите белое вино со словом „сухое“ на этикетке; возьмите штопор и откупорьте бутылку; налейте на дюйм вина в сковороду; включите конфорку под сковородой…» – утомительное расчленение процесса на элементарные шаги, не требующие от читателя принятия мудрых решений, или вынесения тонких суждений, или проявления интуиции.
3. Гарантированный результат: что бы ни делал алгоритм, при безошибочном исполнении он всегда приводит к ожидаемому результату. Алгоритм – рецепт надежный.
Легко видеть, как эти характеристики делают возможным создание компьютера. Любая компьютерная программа является алгоритмом, в конечном счете составленным из простых шагов, которые тот или иной простой механизм может выполнять с невероятной надежностью. Обычно для этого используют электронные микросхемы, но мощность компьютера никак (если не считать скорости вычислительных процессов) не зависит от конкретных особенностей электронов, ударяющихся о силиконовые чипы. Те же самые алгоритмы могут выполняться (и даже еще быстрее) с помощью приборов, в которых фотоны перемещаются по стекловолокну, или (гораздо, гораздо медленнее) командами людей, вооруженных бумагой и карандашами. И, как мы увидим, способность компьютеров с потрясающей скоростью и надежностью выполнять алгоритмы сегодня позволяет ученым-теоретикам исследовать опасную идею Дарвина доселе невозможными методами – и приходить к удивительным результатам.
По сути дела, Дарвин обнаружил не один алгоритм, а скорее большой класс взаимосвязанных алгоритмов, которые он не мог четко различить. Теперь мы можем переформулировать его фундаментальную идею следующим образом:
На протяжении миллиардов лет жизнь на Земле развивалась как единое дерево со множеством ветвей – Древо Жизни; ее развитию способствовали те или иные алгоритмические процессы.
Со временем постепенно (по мере того как мы будем узнавать, какими способами разные люди выражали эту мысль) станет ясно, что означают эти слова. Некоторые формулировки абсолютно пусты и бессодержательны, другие – очевидным образом ложны. Посередине находятся те, что и в самом деле объясняют происхождение видов – и сулят множество других объяснений. Благодаря как упорной критике откровенных ненавистников идеи эволюции как алгоритма, так и опровержениям ее поклонников, такие формулировки становятся все точнее.
5. Процессы как алгоритмы
Размышляя об алгоритмах, теоретики часто подразумевают виды алгоритмов, обладающих свойствами, которых лишены алгоритмы, интересующие нас. Например, когда об алгоритмах размышляют математики, они обычно имеют в виду алгоритмы, относительно которых можно доказать, что они полезны при вычислении конкретных интересующих их математических функций. (Простой пример тому – деление в столбик. В причудливом мире криптографии внимание привлекает разложение большого числа на простые множители.) Но алгоритмы, которые будут интересовать нас, не имеют ничего особенно общего с системой счисления или иными математическими объектами; это алгоритмы классификации, отсева и созидания62.
Поскольку большинство математических обсуждений алгоритмов сосредоточено на их гарантированной или математически доказанной эффективности, люди иногда допускают простейшую ошибку, считая, что процесс, эксплуатирующий случайность или беспорядочность, алгоритмом не является. Но даже при делении в столбик есть место случайности!
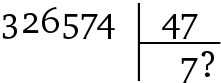
Помещается ли делитель в делимом шесть, семь или восемь раз? Как знать! Да и кому это интересно? Этого и не нужно знать: для того чтобы делить в столбик, большого ума не надо. Алгоритм просто требует, чтобы вы выбрали число – любое, если вам угодно, – и проверили результат. Если избранное число слишком мало, увеличьте его на единицу и начните заново; если оно слишком велико – уменьшите. Относительно деления в столбик можно быть уверенным в одном: оно всегда в конечном счете получается, даже если ваш первоначальный выбор максимально неудачен (в этом случае процесс просто займет немного больше времени). Компьютеры успешно решают сложные задачи несмотря на крайнюю глупость – и именно потому кажутся волшебным изобретением: как что-то настолько безмозглое, как машина, может делать что-то настолько толковое? Итак, не вызывает удивления то, сколь часто интересные алгоритмы используют тактику уточнения выбора, механически проверяя каждого взятого наугад кандидата. Это не только не влияет на их доказуемую эффективность – зачастую именно в этом секрет их эффективности63.
Для начала можно сосредоточиться на группе эволюционных алгоритмов, рассмотрев повседневные алгоритмы, обладающие теми же важными особенностями. Дарвин привлекает наше внимание к повторяющимся волнам соперничества и отбора, так что возьмем обычный алгоритм организации турнира с выбыванием (например, теннисного), который неизбежно венчается четвертьфиналами, полуфиналами и, наконец, финалом, в ходе которого определяется единственный победитель.
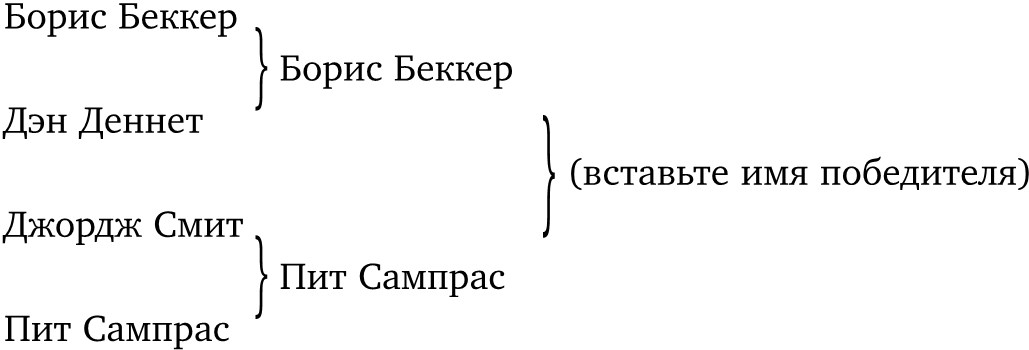
Заметим, что такая процедура удовлетворяет трем условиям. Процедура не изменится, ведем ли мы счет мелом на доске, в компьютерном файле или – необычная возможность – вообще ничего не записываем, а просто осуществляем отбор, веером расположив несколько отгороженных друг от друга теннисных кортов, у каждого из которых две калитки на вход и лишь одна на выход – и через нее победитель попадает на корт, где состоится следующий матч. (А проигравших пристреливают и прикапывают на месте.) Не нужно быть гением, чтобы провести участников состязания через такое «сито», в конце каждого матча заполняя бумаги (или расстреливая проигравших). Алгоритм всегда сработает.
Но что именно он делает? На входе мы имеем некоторое количество участников и гарантию уничтожения для всех, кроме единственного победителя. Но что представляет собой победитель? Это зависит от состязания. Допустим, мы устраиваем не теннисный турнир, а состязание по бросанию монеты. Один из игроков подбрасывает монетку, другой выбирает орла или решку; победитель продвигается на шаг вперед. Победителем такого состязания станет один-единственный игрок, который n раз последовательно победит при подбрасывании монеты, ни разу не проиграв – в зависимости от того, сколько раундов потребуется для завершения состязания.
В таком состязании есть нечто странное и глупое – но что? Победитель и в самом деле обладает весьма примечательным качеством. Часто ли вы встречаете людей, которые, подбрасывая монетку, без единого проигрыша выиграли десять раз подряд? Скорее всего, ни разу. Шансы на появление такого человека могут показаться ничтожными, и при обычном стечении обстоятельств это так и есть. Если какой-нибудь аферист предложит вам побиться об заклад десять к одному, что он сможет привести человека, который у вас на глазах десять раз подряд выиграет в состязании по бросанию монеты (и монета не будет фальшивой), вы, вероятно, склонны будете счесть это пари выигрышным для себя. Если так, будем надеяться, что у этого афериста не нашлось 1024 сообщников (им не придется жульничать – они будут играть абсолютно честно): ведь именно столько (210 участников состязания) нужно, чтобы организовать десятираундный турнир. В начале турнира аферист никак не сможет предсказать, кто именно окажется «вещественным доказательством А», которое обеспечит ему выигрыш пари, но алгоритм проведения турнира неизбежно – и быстро – выявит этого человека: так что вас обманули, и аферист непременно выиграет. (Я не несу ответственности за ущерб, который вы можете понести, попытавшись воспользоваться этим изысканным образчиком практической философии в корыстных целях.)
В любом турнире с выбыванием бывает победитель, который «автоматически» обладает качеством, необходимым, чтобы пройти все этапы состязания, но, как показывает соревнование в бросании монеты, такое качество может быть «всего лишь историческим» – банальным фактом биографии участника состязания, никак не влияющим на его или ее виды на будущее. Представим, например, что ООН принимает постановление впредь разрешать все международные конфликты, подбрасывая монетку, – участвовать в таком соревновании должны представители конфликтующих сторон (если в конфликт вовлечено более одного народа, придется организовывать какой-то турнир: можно использовать круговую систему – алгоритм тогда будет другим). Кого следует выбрать представителем нашей нации? Естественно, того, кто лучше всех бросает монетку. Допустим, мы организовали масштабный турнир с выбыванием, в котором принимают участие все мужчины, женщины и дети США. Кто-то в нем победит – этот человек последовательно выиграет в двадцати восьми раундах без единого проигрыша. Победа будет неопровержимым фактом его биографии, но, поскольку подбрасывание монеты – дело случая, нет никаких оснований полагать, что победитель такого турнира покажет себя на международных соревнованиях лучше, чем кто-либо, проигравший в одном из предыдущих раундов. У случая нет памяти. Человек, у которого в руках выигрышный лотерейный билет, безусловно, был удачлив, и благодаря только что выигранным миллионам удача ему может больше никогда не понадобиться; тем лучше, ведь нет оснований считать, что его шансы во второй раз выиграть в лотерею выше, чем у любого другого участника – или что, скажи он «орел», монета упадет загаданной стороной вверх. (Неспособность принять тот факт, что у случая нет памяти, известна как ошибка игрока; это заблуждение удивительно широко распространено – настолько широко, что мне, вероятно, следует подчеркнуть, что это – без всяких сомнений и оговорок – заблуждение.)
В противоположность соревнованиям, где правит случай (например, соревнованиям в бросании монеты), существуют соревнования, где все решает мастерство – например, теннисные турниры. Здесь есть основания полагать, что игроки, вышедшие в последние раунды, снова преуспеют, если выставить их против тех, кто вылетел из состязания раньше. Есть основания – но никаких гарантий – полагать, что победитель такого турнира – самый лучший игрок и будет лучшим не только сегодня, но и завтра. Тем не менее, хотя любой разумно организованный турнир неизбежно позволит назвать победителя, нет гарантий, что в ходе состязания в мастерстве победитель окажется лучшим игроком во всех (значимых) смыслах этого слова. Вот почему на церемонии открытия мы иногда говорим: «Пусть победит сильнейший!» – процедура не гарантирует подобный исход. Лучший игрок – тот, кто является лучшим по «техническим» критериям (обладатель самого мощного удара левой, самой быстрой подачи, самой высокой выносливости и т. д.), – может встать не с той ноги, вывихнуть лодыжку – или его может ударить молния. Тогда, очевидно, в состязании его обойдет игрок похуже. Но никто не станет организовывать или участвовать в соревнованиях в мастерстве, если бы в конце концов их не выигрывали лучшие игроки. Это гарантирует само определение честного состязания в мастерстве; если бы лучшие игроки выигрывали в каждом раунде с вероятностью не выше 50%, речь шла бы о состязании в удачливости, а не в мастерстве.





